Формула чистая текущая стоимость проекта: Чистая текущая стоимость (NPV)

Текущая дисконтированная стоимость

Текущая дисконтированная стоимость

25.07.2022

Текущая дисконтированная стоимость определяется как финансовое состояние, необходимое в настоящее время, чтобы иметь нужную прибыль в будущем на определенных условиях.

Руководящий состав должен хорошо понимать движение денежных средств в организации. Текущая дисконтированная стоимость способствует формированию объективного анализа ситуации, помогает рассчитать сроки окупаемости. Текущая дисконтированная стоимость влияет на статус фирмы. Состояние компании оценивается по объемам и составу активов, чистой прибыли и обязательствам на конкретную дату. Активы, обязательства постоянно корректируются, приводятся в соответствие к текущей дисконтированной стоимостью. Финансовое положение компании отражается в отчетах. Конечный результат не зависит от применения дисконтирования, но влияет на структуру итогов и выделение процентной ставки.

Текущая дисконтированная стоимость определяется по формуле:

• PV=FV/(1+i)t ∙ PV – текущая дисконтированная стоимость;
• FV – ожидаемая сумма;
• i – процентная ставка вложений;
• t – временной период вложения.

Когда предприятие знает, как происходит движение денежных средств, рассчитывается сумма будущего финансового периода при нынешней ситуации: FV = PV*(1+i)t

Для расчета ожидаемой прибыли применяется чистая текущая дисконтированная стоимость. С ее помощью можно увидеть результат, исключая затраченные средства. Расчет срока окупаемости проекта актуален в большей степени при крупных финансах. Текущая дисконтированная стоимость помогает определить эффективность вложений. С ее помощью можно легко рассчитать и рассмотреть предложения, в которых получится быстрая отдача от вложенных инвестиций за определенный временной период. Опираясь на данные текущей дисконтированной стоимости пересчитывается дебиторская и кредиторская задолженность.

Компаниям выгодно заключать долговременные контракты на условиях отсрочки платежа. Одна из причин — инфляция, которая ведет к обесцениванию денежных знаков и автоматическому уменьшению суммы долга перед поставщиками и банками. Если заказы делаются с хозяйственным подходом, у предприятия получается огромная экономия с учетом заключенных контрактов на большие суммы.

Текущая дисконтированная стоимость оказывает помощь одновременно поставщику и покупателю. При оформлении договоров необходимо предвидеть инфляцию и учитывать дополнительные проценты к сумме при задержке выплаты. Взвешенный экономический подход поможет выработать эффективную стратегию предприятия и сделать выгодные инвестиции.

Текущая дисконтированная стоимость используется для исчисления баланса:

• амортизация займов и дебиторской задолженности, инвестиций, удерживаемых до погашения, и обязательств, отражаемых по амортизации;
• стоимость обесценения некотируемых долевых рычагов, которые не принимаются во внимание по справедливой стоимости, т.к. справедливая стоимость не может быть надежно оценена;
• справедливая стоимость активов, отражаемых по справедливой стоимости через прибыль или убыток, и активов, имеющихся в наличии для продажи, в случае применения доходного подхода к определению справедливой стоимости;
• стоимость резервов, определяемых как ответственность с неопределенным сроком исполнения или неопределенной величины, в случаях, когда влияние фактора времени на стоимость денег существенно;
• стоимость исполнение по пенсионным планам и обязательств по вознаграждениям по окончании трудовой деятельности;
• стоимость чистых инвестиций в аренду.

Используя текущую дисконтированную стоимость, компания видит возможные пробуксовки при расчетах и пути вложения денежных средств самым выгодным способом.

Хотите сократить количество новостных рассылок в 2 раза?

Все, что нужно, в одном письме!

Подпишитесь на нашу ежемесячную новостную рассылку, в которой мы говорим только о самых главных событиях отрасли и законодательства. Материалы пишут исключительно профессиональные аудиторы, юристы, оценщики и налоговые консультанты.

Ваша заявка
успешно отправлена!

В ближайшее время с Вами свяжется наш менеджер.

Мы используем файлы cookie:

Пользуясь настоящим веб-сайтом, Вы даете свое согласие на использование файлов cookies.

Узнать подробнее >

Ставка дисконтирования: что это, где применить и как рассчитать

Что такое ставка дисконтирования, для чего она нужна и как ее рассчитывать. Рассказываем об этом в нашем обзоре

Фото: Shutterstock

В этой статье вы узнаете

1. Что это
2. Как появилась
3. Как рассчитать
4. Интуитивные методы определения ставки
5. Модели расчета на основе премий за риск
6. Аналитические методы расчета
7. Как применяется

Что такое ставка дисконтирования

www. adv.rbc.ru

Ставка дисконтирования — это эталонная величина, выраженная в процентах, применяемая для сравнительной оценки эффективности инвестиций.

Например, вам нужно выбрать: положить деньги в банк со ставкой депозита 12% сроком на пять лет с ежегодной выплатой процента или купить облигации  с погашением через девять лет с купоном 8,5%, выплачиваемым дважды в год и с текущей ценой 91% от номинала. Как вы будете выбирать, да еще учитывая, что уровень инфляции составляет около 8%?

Аналитик занимается оценкой стоимости (Фото: Shutterstock)

Для решения этих задач используется прием, который называют

дисконтированием. С помощью дисконтирования можно сопоставить будущие денежные потоки и выбрать из нескольких вариантов инвестиций самый выгодный. А ставка дисконтирования — это ключевой элемент, используемый в приеме дисконтирования.

Правильный расчет ставки дисконтирования позволит вам:

• оценить эффективность инвестиций относительно надежных вкладов;
• сравнить варианты инвестиций с разной длительностью вложения;
• сравнивать доходность вложений инструментов с разной степенью риска.

Ставка дисконтирования зависит от множества факторов: уровень инфляции, доступные для инвестора варианты вложений, риск вложений, стоимость вашего капитала и др. Но далеко не все внешние факторы можно достоверно учесть в ставке.

Как появилась ставка дисконтирования

Первоначально ставка дисконтирования применялась при учете векселей. Принимая к оплате вексель, банкиры знали сумму, которую они получат, когда предъявят вексель к погашению. Но чтобы им самим заработать, банкиры выплачивали предъявителю деньги со скидкой — дисконтом. А процентная ставка, в которой измерялся их доход, называлась учетной ставкой, или ставкой дисконтирования (discount rate). Сумма, которая выплачивалась предъявителю векселя, рассчитывалась как раз с помощью дисконтирования — зная, сколько он получит в будущем и учитывая текущий уровень процентных ставок, банкир определял текущую стоимость денег.

Этот прием оказался настолько универсальным и полезным, что стал широко применяться при оценке и сравнении эффективности вложений в разные инструменты или проекты. При дисконтировании инвестор, как и банкир при учете векселей, пересчитывает стоимость денег, которые он получит в будущем, причем в совершенно разные сроки, на текущую стоимость. Он как бы проецирует стоимость денег из будущего на плоскость настоящего времени. А центральным звеном расчетов выступает ставка дисконтирования.

Как рассчитать ставку дисконтирования

При расчете ставки дисконтирования очень важно определить ставку, которая позволит максимально корректно привести будущую стоимость доходов и расходов к текущей. Для этого нужно учитывать и общий уровень процентных ставок, и факторы риска вложений в отдельные инструменты.

При расчете ставки дисконтирования нужно учесть два основных вида факторов:

1. Уровень безрисковых ставок.
2. Премии за риск.

Безрисковые ставки

 — это процентные ставки инструментов с минимальным для инвестора уровнем риска. Обычно такими инструментами являются облигации центрального правительства — ОФЗ в России, US Treasuries в США и т. п. Также в качестве безрисковых ставок могут учитываться ставки по депозитам системообразующих банков. Иногда как безрисковая ставка может рассматриваться ключевая ставка центральных банков.

Уровень безрисковых ставок является фундаментальным — он определяет минимальный уровень всех ставок дисконтирования.

Премии за риск — это надбавки к уровню безрисковых ставок, которые стоит учитывать при вложении в отдельные инструменты или проекты. Это могут быть общие факторы — уровень инфляции, надбавка за страновой риск; факторы, учитывающие риск вложения в отдельные инструменты, — надбавка за отраслевой риск, надбавка за индивидуальный риск (зависит от надежности эмитента, инструмента или проекта).

Учет премий за риск позволит более точно настроить инструмент дисконтирования, чтобы избежать ошибок в сравнении разных инвестиций.

При расчете ставки дисконтирования используются различные способы и методы, которые можно объединить в такие основные группы:

• интуитивные методы;
• модели на основе премий за риск;
• аналитические модели.

Интуитивные методы

В эту группу включается:

• собственно интуитивный метод.
• экспертный метод.

Интуитивный метод — это способ определения ставки дисконтирования на основе субъективного видения инвестора. Проще говоря, когда инвестор прикидывает ставку дисконтирования практически на глазок. Например, он рассуждает так: «Я могу положить деньги на депозит в надежном банке под 12–15%. Тогда эффективность других вложений я буду сравнивать с таким уровнем ставок».

Экспертный метод — это, по сути, тот же интуитивный метод, только итоговая величина ставки дисконтирования выводится как совокупный консенсус нескольких экспертов с тем или иным уровнем обоснованности их мнений.

Аналитики совещаются (Фото: Shutterstock)

Модели на основе премий за риск

К моделям на основе премий за риск относятся, например, такие модели, как:

• модель кумулятивного построения;
• модель капитальных активов CAPM.

Общим для этих моделей является то, что ставка дисконтирования выводится как сумма безрисковой ставки и премий за риск.

Модели кумулятивного построения — это метод определения ставки дисконтирования, при котором к безрисковой процентной ставке прибавляются все премии за риск, которые можно определить для конкретного инструмента.

Формула расчета ставки дисконтирования кумулятивным способом выглядит так:

где r0 — безрисковая ставка,

r1, r2, rn — все премии за риск для оцениваемого инструмента.

Модель капитальных активов CAPM (Capital Asset Pricing Model, модель оценки капитальных активов) — это метод определения ставки дисконтирования для сравнительной оценки эффективности вложений в акции, при котором к безрисковой процентной ставке прибавляется премия за риск по отдельному инструменту с учетом его β-коэффициента.

β-коэффициент (бета-коэффициент) — это мера рыночного риска акции, которая показывает изменчивость доходности акции к доходности на рынке в среднем. β-коэффициент численно показывает, на сколько процентов изменяется цена акции бумаги при росте или снижении индекса на 1%. Положительный коэффициент говорит о том, что акция двигается в одном направлении с рынком, а отрицательный коэффициент означает, что акция двигается в противоположную от общего направления рынка сторону.

β-коэффициенты рассчитываются и публикуются и аналитиками, и торговыми площадками, например Московской биржей.

Формула расчета ставки дисконтирования по CAPM выглядит так:

где r0 — безрисковая ставка,

β — β-коэффициент,

rf — средняя доходность фондового рынка (биржевого индекса).

Аналитические диаграммы (Фото: Shutterstock)

Аналитические методы

Аналитические методы — способы расчета ставки дисконтирования с применением элементов финансового анализа.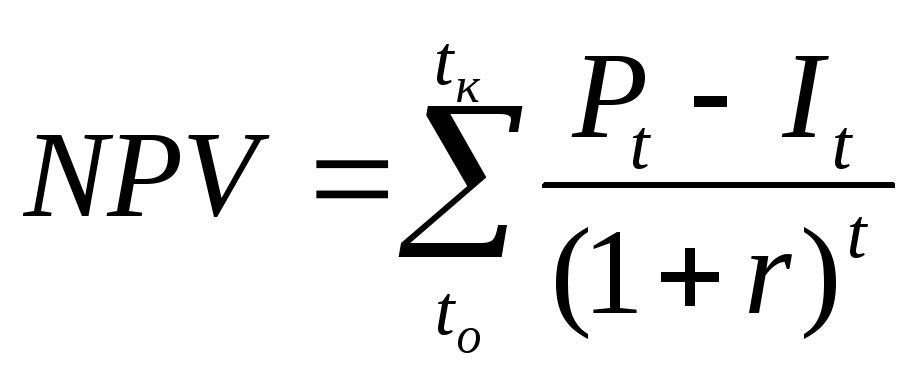 Среди аналитических методов можно выделить:

• WACC;
• мультипликативные методы.

WACC — это средневзвешенная стоимость капитала (Weighted Average Cost of Capital). WACC используется компаниями для сравнительной оценки эффективности инвестиционных проектов.

Как правило, у компании есть два вида используемого капитала — собственный и заемный. Собственный капитал равен сумме средств, принадлежащих самой компании или причитающихся ее акционерам. Заемный капитал — это средства, привлеченные компанией извне (кредиты и займы). Заемный капитал достается компании не бесплатно — по кредитам и займам она должна платить проценты.

В случае когда у компании или у инвестора только заемные деньги, то для них самым главным становится то, чтобы инвестиционные проекты приносили больше, чем приходится платить по кредиту. В этом случае при оценке инвестиционных проектов в качестве ставки дисконтирования можно использовать ставку по кредиту, скорректированную на ставку налога на прибыль.

Но когда у компании есть и собственный, и заемный капитал, то ставка дисконтирования по модели WACC считается следующим образом:

где re — стоимость собственного капитала,

Se — доля собственного капитала,

rd — стоимость заемного капитала,

Sd — доля заемного капитала,

t — ставка налога на прибыль.

Стоимость заемного капитала rd — это средневзвешенный процент по имеющимся займам и кредитам.

Стоимость собственного капитала re может определяться либо методом CAPM, описанным выше, либо другим способом — например, с помощью модели Гордона.

Модель Гордона для оценки стоимости собственного капитала компании предполагает, что за возможность использования собственного капитала компания платит дивидендами. Значит, стоимость собственного капитала определяется отношением суммы выплаченных дивидендов к сумме денег, привлеченных в ходе размещения акций.

В итоге формула, по которой рассчитывается стоимость собственного капитала по Гордону, выглядит так:

где DIV — это сумма годовых ожидаемых дивидендов на одну акцию;

P — цена размещения акций,

fc — затраты на эмиссию (в %),

g — темпы прироста дивидендов.

Мультипликативные методы — это способы расчета ставки дисконтирования на основе различных коэффициентов прироста и других коэффициентов предприятий.

Это может быть, например:

• расчет ставки на основе рентабельности капитала (ROE), когда за ставку дисконтирования принимают показатель ROE;
• расчет ставки на основе рентабельности активов (ROA), когда за ставку дисконтирования принимают показатель ROA;
• расчет ставки на основе рыночных мультипликаторов, когда за ставку дисконтирования принимают значение доходности как отношения прогнозного дохода к текущей рыночной стоимости компании. Например, прогнозное значение чистой прибыли на акцию (EPS) к рыночной стоимости акций или прогнозное значение денежного потока к капитализации

Как применяется ставка дисконтирования

Как мы писали вначале, ставка дисконтирования — это ключевой элемент, используемый в приеме дисконтирования.

Дисконтирование — это приведение будущей стоимости денежных потоков к стоимости в настоящее время по ставке дисконтирования.

Один из частых результатов дисконтирования — получение чистой текущей (приведенной) стоимости денег.

Чистая текущая стоимость (NPV, Net Present Value) — разница между всеми денежными притоками и оттоками, приведенными к текущему моменту времени по ставке дисконтирования. Эта величина показывает сумму денежных средств, которую инвестор ожидает получить от проекта, пересчитанную к настоящему времени.

Сравнив NPV разных по длительности инвестиционных вариантов, инвестор может выбрать наиболее доходный.

Узнайте о возможностях нашего Каталога в телеграм-канале «РБК Инвестиций»

Долговая ценная бумага, владелец которой имеет право получить от выпустившего облигацию лица, ее номинальную стоимость в оговоренный срок. Помимо этого облигация предполагает право владельца получать процент от ее номинальной стоимости либо иные имущественные права. Облигации являются эквивалентом займа и по своему принципу схожи с процессом кредитования. Выпускать облигации могут как государства, так и частные компании.

Формула чистой приведенной стоимости | Примеры с шаблоном Excel

Формула чистой приведенной стоимости (оглавление)

• Формула
• Примеры

Чистая приведенная стоимость — это приведенная стоимость всех притоков и оттоков денежных средств по проекту за определенный период времени. Формула чистой приведенной стоимости приведена ниже:

NPV = ∑(CF _n / (1 + i) ⁿ ) – Первоначальные инвестиции

Где,

• n = Период, который принимает значения от 0 до n-го периода до окончания периода денежных потоков
• CF _n = Денежный поток в n-м периоде
• i = Ставка дисконтирования

Примеры формулы чистой приведенной стоимости (с шаблоном Excel)

Давайте рассмотрим пример, чтобы лучше понять расчет чистой приведенной стоимости.

Вы можете скачать этот шаблон Excel с формулой чистой приведенной стоимости здесь — Формула чистой приведенной стоимости Excel, шаблон

Формула чистой приведенной стоимости – Пример №1

Предположим, что первоначальный денежный поток для проекта составляет 10 000 долларов США, инвестированных в проект, а последующие денежные потоки за каждый год в течение 5 лет составляют 3 000 долларов США. Ставка дисконтирования принимается равной 10%. Рассчитать чистую текущую стоимость.

Решение:

Сначала мы должны вычислить текущую стоимость

Результат будет: должны вычислить его для других значений.

Чистая приведенная стоимость рассчитывается по формуле, приведенной ниже 003

• NPV = (2 727,27 долл. США + 2 479,34 долл. США + 2 253,94 доллара США + 2 049,04 доллара США + 1 862,76 доллара США) – 10 000 долларов США
• NPV = 1372,36 долл. США

Формула чистой приведенной стоимости – Пример №2

General Electric имеет возможность инвестировать в 2 проекта. Проект А требует инвестиций в размере 1 млн долларов США, которые будут приносить доход в размере 300 000 долларов США каждый год в течение 5 лет. Проект B требует инвестиций в размере 750 000 долларов США, которые дадут доход в размере 100 000 долларов США, 150 000 долларов США, 200 000 долларов США, 250 000 долларов США и 250 000 долларов США в течение следующих 5 лет. Затем рассчитайте чистую текущую стоимость, которую можно использовать, чтобы решить, какая возможность лучше и в которую следует инвестировать.

Примечание: Чистая приведенная стоимость используется компаниями при принятии решений о бюджете капиталовложений, чтобы решить, какие инвестиции они предпочли бы сделать. На основании результатов чистой приведенной стоимости компания может принять решение об инвестировании в один проект и отказе от другого.

Для проекта A

Решение:

Во-первых, мы должны рассчитать коэффициент дисконтирования

Результат будет: 9000 3

Аналогичным образом мы должны вычислить его для других значений.

Чистая приведенная стоимость рассчитывается по формуле, приведенной ниже 0003

• NPV = (272 727,27 долл. США + 247 933,88 долл. США + 225 394,44 долл. США + 204 904,04 долл. США + 186 276,40 долл. США) – 1 000 000 долл. США
• NPV = $137 236

Для проекта B

Решение:

Во-первых, мы должны рассчитать коэффициент дисконтирования.

Результат будет:

Точно так же мы должны вычислить его для других значений.

Чистая приведенная стоимость рассчитывается по формуле, приведенной ниже 0003

• NPV = (90 909,09 долл. США + 123 966,94 долл. США + 150 262,96 доллара США + 170 753,36 доллара США + 155 230,33 доллара США) – 750 000 долларов США
• NPV = -58 877 долларов

Следовательно, General Electric должна выбрать проект A.

Формула чистой приведенной стоимости – пример №3

Формула чистой приведенной стоимости часто используется в качестве механизма для оценки корпоративной стоимости компании. Прогнозируемые доходы от продаж и другие статьи расходов для компании можно использовать для оценки свободных денежных потоков компании и использования средневзвешенной стоимости капитала (WACC) для дисконтирования этих свободных денежных потоков для получения стоимости компании.

Например: –

Для Apple Inc. ниже приведены расчетные статьи прибылей и убытков на следующие 5 лет. Рассчитать чистую текущую стоимость.

Решение:

FCFF рассчитывается по формуле, приведенной ниже 03

При условии WACC @ 10%

Предполагая, что g является устойчивым ростом экономики на уровне 3%.

Конечная стоимость оценивается по мере того, как компания будет продолжать свою деятельность после 5-го года: –

Конечная стоимость рассчитывается по формуле, приведенной ниже

Конечная стоимость = FCFF ₅ (1 + g) / (WACC – g)

• Конечная стоимость = 135 000 долл. США * (1 + 3%) / (10% – 3%)
• Конечная стоимость = $1 986 428,6

Чистая текущая стоимость рассчитывается по приведенной ниже формуле

NPV = ∑(CF _n / (1 + i) ⁿ ) – Начальные инвестиции

• NPV = (8 181,8 долл. США + 33,47 долл. США 1,1 + 54 094,7 доллара США + 70 691,9 доллара США + 1 368 415,9 доллара США) – 1 000 000 долларов США
• NPV = $534 855

Объяснение

Чистую текущую стоимость можно рассматривать как метод расчета рентабельности инвестиций в ваш проект. Он используется для определения возврата будущих денежных потоков, которые будут начислены компанией на сегодняшние инвестиции. Следовательно, важно дисконтировать денежные потоки, потому что доллар, заработанный в будущем, не будет стоить столько сегодня. Компонент временной стоимости важен, потому что из-за различных факторов, таких как инфляция, процентные ставки и альтернативные издержки, деньги, полученные раньше, более ценны, чем деньги, полученные позже.

Точно так же, чем рискованнее инвестиции, тем больше коэффициент дисконтирования. Некоторым инвестициям изначально присущ более высокий риск, и, следовательно, при оценке приведенной стоимости следует использовать более высокий коэффициент дисконтирования для оценки таких инвестиций.

Релевантность и использование формулы чистой приведенной стоимости

Метод чистой приведенной стоимости имеет несколько пользователей. Чистая приведенная стоимость используется компаниями для оценки своих инвестиций и определения того, стоит ли продолжать определенный проект. Он также используется инвесторами для оценки общей стоимости компании или стоимости акционерного капитала, а также для определения того, стоит ли в них инвестировать или нет.

Ключевое преимущество использования NPV заключается в том, что он дает нам прямую меру ожидаемого увеличения стоимости любой компании. Существуют и другие методы, такие как IRR, период окупаемости и т. д., чтобы определить, следует ли делать инвестиции или нет, но NPV, безусловно, является лучшим показателем получения прямой выгоды от инвестиций.

Он также имеет свои недостатки, такие как чистая приведенная стоимость не учитывает размер проекта. Например, чистая приведенная стоимость в размере 100 долларов США для инвестиций в размере 100 долларов США является стоящей инвестицией, но чистая приведенная стоимость в размере 100 долларов США для инвестиций в размере 1 миллиона долларов США, хотя и должна рассматриваться как положительная, стоит ли инвестировать в нее или нет.

Заключение

Чистая приведенная стоимость — это выбранная форма оценки любой инвестиционной возможности, поскольку она обеспечивает прямое измерение ожидаемой выгоды. Он учитывает временную стоимость денег, что является важным понятием и может использоваться в целом для сравнения аналогичных инвестиций и выбора альтернатив. Это не лишено недостатков, таких как множество предположений, которые необходимо сделать, чтобы получить выгоду от инвестирования в возможность.

Рекомендуемые артикулы

Это руководство по формуле чистой приведенной стоимости. Здесь мы обсуждаем, как рассчитать чистую приведенную стоимость, а также практические примеры и загружаемый шаблон Excel. Вы также можете прочитать следующие статьи, чтобы узнать больше –

1. Примеры формулы коэффициента Джини
2. Калькулятор формулы реального ВВП
3. Формула среднего арифметического | Шаблон Excel
4. Формула доли рынка | Определение | Примеры

Чистая текущая стоимость, соотношение выгод и затрат и коэффициент текущей стоимости для оценки проекта

Печать

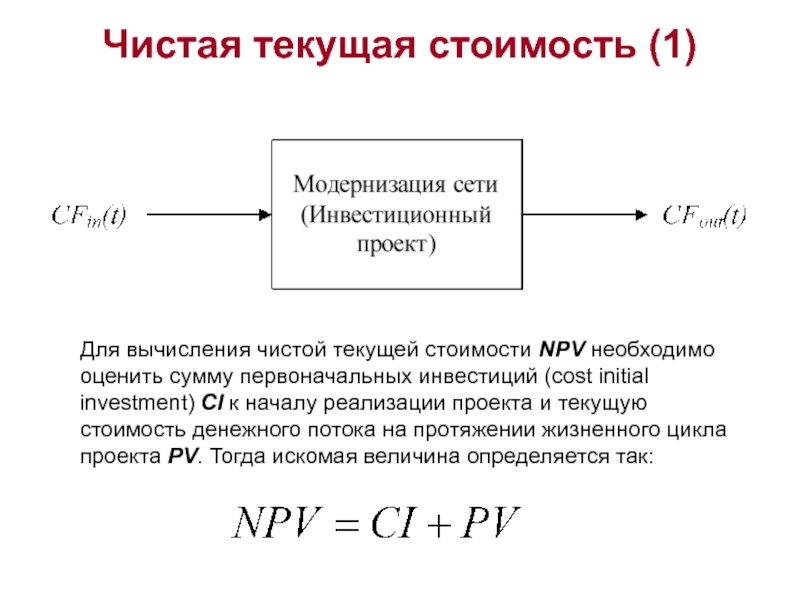
Чистая приведенная стоимость (NPV)

Как объяснялось в первом уроке, Чистая приведенная стоимость (NPV) представляет собой совокупную приведенную стоимость положительного и отрицательного инвестиционного денежного потока с использованием определенной ставки для обработки временной стоимости денег. .

NPV=текущая стоимость доходов или сбережений @i*-текущая стоимость затрат @i*

или

NPV=чистая текущая стоимость положительного и отрицательного денежного потока @i*

90 002 или

NPV = Текущая стоимость всех наличных денег Потоки @i*

Если расчетная чистая приведенная стоимость проекта положительна, то проект удовлетворительный, а если чистая приведенная стоимость отрицательная, то проект неудовлетворительный.

Следующее видео, функция NPV в Excel , объясняет, как вычислить NPV с помощью Microsoft Excel (8:04).

Функция NPV в Excel

Нажмите, чтобы просмотреть расшифровку видео «Функция NPV в Excel».

ВЕДУЩИЙ: В этом видео я объясню, как использовать функцию NPV в Excel для расчета NPV денежного потока. Существует два основных способа вызова функции NPV в Excel. Первый способ — щелкнуть вот этот маленький Fx. Когда вы нажимаете на нее, появляется это окно, и вы можете искать функцию NPV в этом поле.

Вы нажимаете «Перейти». Он находит функцию NPV, или вы можете перейти в категорию «Финансы» здесь, и вы найдете функцию NPV. И затем вы нажимаете ОК.

Здесь вы видите три коробки. Первый просит вас ввести Rate. Эта ставка представляет собой процентную ставку, по которой вы собираетесь дисконтировать свой денежный поток при расчете чистой приведенной стоимости. Вы можете написать здесь число, которое будет составлять 10%, или вы можете оценить их из ячейки, которую я написал здесь 10%. Затем после этого мы можем щелкнуть по этому или нажать Enter.

И после этого вы можете ввести денежный поток. Вы можете ввести денежный поток по одному в каждом из этих значений или выбрать здесь денежный поток в виде серии. Затем нажмите здесь. Если вы все ввели правильно, будет рассчитана чистая приведенная стоимость, и функция отобразит здесь чистую приведенную стоимость. Если что-то не так, вы не увидите здесь правильную NPV. Затем я нажимаю ОК. Итак, как видите, чистая приведенная стоимость рассчитана и показана.

Другой способ вызова функции NPV заключается в том, что вы просто пишете знак равенства, а затем пишете открывающие скобки NPV, первую, и тогда вы можете видеть, появляется ли эта штука. В первом нужно ввести ставку. Вы можете написать значение здесь — вы можете написать 10%, или вы можете прочитать его из этой ячейки. А потом пишешь запятую, а потом вводишь значения. Вы начинаете отсюда, идете до конца денежного потока. А ты закрываешь скобки.

Итак, одна вещь, с которой вы должны быть очень осторожны, используя функцию NPV в Excel, — это функция NPV в Excel, которая всегда считает, что вы вводите свой денежный поток с первого года. Итак, если у вас есть денежный поток, который происходит в настоящее время, в момент времени 0— в год 0— вы должны ввести это вручную. Функция NPV в Excel не учитывает никакого денежного потока в момент времени 0 — она не понимает время 0. NPV предполагает, что вы вводите все, начиная с года 1.

Таким образом, вы всегда можете перепроверить результат этой функции NPV. . Если вы рассчитаете приведенную стоимость каждого из этих платежей, сумма этого дисконтированного денежного потока должна быть равна этой чистой приведенной стоимости. Давайте быстро посчитаем это. Допустим, мы хотим рассчитать текущую стоимость этих платежей. Первый равен 50 000 долларов, разделенным на 1 плюс процентная ставка. Я поставил знак доллара позади столбца, чтобы исправить это, когда я собираюсь применить его к другим ячейкам и мощности, году.

Итак, как вы можете здесь видеть, это текущая стоимость инвестиций в размере 50 000 долларов. Я применяю это к другим ячейкам. Таким образом, сумма этого дисконтированного денежного потока, этих приведенных значений должна быть точно такой же, как чистая приведенная стоимость, которую мы рассчитали с помощью функции чистой приведенной стоимости в Excel, и вы можете видеть, что они точно такие же.

Итак, давайте поработаем над другим примером, который имеет денежный поток в настоящее время. Итак, как вы можете видеть в этой инвестиции, у нас будет 60 000 долларов инвестиций в настоящее время, а также 50 000 долларов инвестиций в первый год. Эти инвестиции будут приносить годовой доход в размере 24 000 долларов США в год со 2 по 10 год. Давайте посмотрим, как мы можем рассчитать чистую приведенную стоимость этого денежного потока, используя функцию чистой приведенной стоимости в Excel.

Как вы видите здесь, поскольку в настоящее время у нас будет платеж, нам нужно ввести этот платеж вручную. Итак, что мы делаем, так это пишем знак равенства, а затем добавляем этот платеж, который происходит в настоящее время, или год 0. А затем после этого мы используем функцию NPV для остальной части денежного потока. Я пишу NPV— я оцениваю процентную ставку отсюда. Затем я выбираю денежный поток, начиная с года 1 и заканчивая годом 10. Я закрываю скобки и нажимаю Enter. Итак, это чистая приведенная стоимость, использующая функцию чистой приведенной стоимости этого денежного потока.

Давайте перепроверим наш результат. Давайте посмотрим, правильно это или нет. Итак, я собираюсь рассчитать текущую стоимость всех этих платежей, а затем сумма должна быть точно такой же, как и эта чистая приведенная стоимость, используя функцию чистой приведенной стоимости. Таким образом, текущая стоимость равняется этому платежу — он происходит в настоящее время, поэтому его не нужно сбрасывать со счетов. Таким образом, это равна той же сумме — приведенная стоимость этого, 50 000 долларов, равна 50 000 долларов, деленная на 1 в открытых скобках плюс процентная ставка. Я фиксирую столбец, чтобы убедиться, что он не изменится, чтобы процентные ставки продажи не изменились, когда я собираюсь применить к другим ячейкам. Я закрываю скобки и мощность, год. Итак, это текущая стоимость этого — 50 000 долларов в год 1.

Итак, я применяю это к остальным денежным потокам, и суммирование этого дисконтированного денежного потока должно дать мне то же значение, что и ЧПС, которую я использовал с помощью функции ЧПС в Excel. Как мы видим, они абсолютно одинаковы.

Итак, это два способа расчета NPV с помощью Excel, и как мы можем перепроверить другой.

Авторы и права: Farid Tayari

В видео NPV и IRR в Excel 2010 (8:59) вы можете найти еще одно полезное видео для расчета NPV с использованием функции Excel NPV. В этом видео денежный поток отформатирован в вертикальном направлении (нет абсолютно никакой разницы между вертикальным и горизонтальным форматированием, с использованием электронных таблиц).

В следующем видео, функция IRR в Excel , я объясняю, как рассчитать норму прибыли для данного денежного потока с помощью функции Microsoft Excel IRR (4:19).

Функция IRR в Excel

Нажмите, чтобы просмотреть расшифровку видео «Функция IRR в Excel».

ВЕДУЩИЙ: В этом видео я собираюсь объяснить, как рассчитать норму прибыли для данного денежного потока, используя функцию IRR в Excel. Есть два способа вызвать функцию IRR. Во-первых, мы можем нажать на этот значок fx. Это всплывающее окно, и мы можем написать IRR в этом поле, которое является окном поиска. Иди, найдет. Или мы можем выбрать финансовый из этого списка и найти IRR.

Когда мы выбираем IRR, открывается это окно. И у него две коробки. В первом поле нужно, чтобы вы ввели денежный поток. В вызове функции Excel IRR есть очень важный момент. Это требует от вас ввода денежного потока и предполагает, что ваш денежный поток начинается с нулевого года. Поэтому вы должны быть очень осторожны, используя функцию IRR в Excel. Предполагается, что ваш денежный поток начинается с нулевого года или в настоящее время.

Итак, я выбираю денежный поток, начиная с нулевого года. И я нажимаю здесь или нажимаю Enter. Так вот, он уже рассчитал IRR. Но иногда функция IRR не может найти норму прибыли. Поэтому вам нужно дать ему начальное предположение. Если у вас нет никаких предположений, просто дайте им 10%. Если он все еще не вычисляет его, дайте ему 20% и так далее. И нажимаешь ОК. Итак, как вы можете видеть здесь, норма прибыли для этого денежного потока, начиная с нулевого года, составляет 14,06%.

Другой способ вызвать функцию IRR в Excel — просто написать функцию IRR. Вы пишете знак равенства, а затем пишете IRR. Вы можете видеть, что Excel показывает это здесь, показывает функцию здесь. Вы раскрываете скобки. Вы выбираете денежный поток, начиная с нулевого года и заканчивая 10 годом. Запятая и начальное предположение, которое будет составлять 10%. И результат.

Таким образом, мы всегда можем перепроверить этот результат, который мы рассчитали с помощью функции Excel IRR. Как известно, норма доходности — это ставка, при которой NPV равна нулю. Поэтому, если я вычислю NPV для этой ставки, она должна быть равна нулю или очень близка к нулю. Итак, давайте посмотрим. Рассчитаем NPV для этой ставки.

Так как в настоящее время у нас будет платеж, я должен ввести этот платеж вручную. Затем я должен рассчитать чистую приведенную стоимость остальных денежных потоков, начинающихся с первого года, с помощью функции чистой приведенной стоимости.

NPV, открытые скобки. Ставки. Я выбираю тариф. Запятая, а затем я выбираю денежный поток, который начинается с первого года. И закрываю скобки. И вы можете видеть, что NPV равна нулю. Таким образом, это показывает, что норма прибыли, которую я рассчитал для этого денежного потока, верна.

Кредит: Фарид Тайари

Пример 3-6:

Пожалуйста, рассчитайте чистую приведенную стоимость для следующего денежного потока, учитывая минимальную ставку дисконтирования 10% и 15%.

С =60 000	С =50 000	I =24 000	I =24 000	. ..	I =24 000
0	1	2	3	…	10

C: Затраты, I: Доход

i*=10%: NPV=-60 000–50 000*(P/F10%,1)+24 000*(P/F10%,1)*(P/ A10%,9)=20 196,88 долларов СШАi*=15%: NPV=−60 000–50 000*(P/F15%,1)+24 000*(P/F15%,1)*(P/A15%,9) =– 3 897,38 долл. США

При использовании электронной таблицы следующий метод может быть более удобным:

i*=10%: NPV=−60 000–50 000*(P/F10%,1)+24 000*(P/F10%,2)+24 000 *(P/F10%,3)+…+24,000*(P/F10%,10)=20,19$6,88i*=15%: NPV=-60 000–50 000*(P/F15%,1)+24 000*(P/F15%,2)+24 000*(P/F15%,3)+… +24 000 *(P/F15%,10)=-$3897,38

На рис. 3-5 показано вычисление функции NPV в Microsoft Excel. Обратите внимание, что для использования функции NPV в Microsoft Excel все затраты необходимо вводить с отрицательными знаками. Рисунок 3-5: Расчет NPV в Microsoft Excel чистого положительного денежного потока, деленного на чистый отрицательный денежный поток в точке i*.

Коэффициент затрат и выгод = PV чистого положительного денежного потока/PV чистого отрицательного денежного потока

Уравнение 3-1

Уравнение 3-1

03

Если B/C >1, то проект (s) является экономически удовлетворительным
Если B/C =1, то проект(ы) экономическая безубыточность проекта аналогична другим проектам (с той же ставкой дисконтирования или нормой прибыли)
Если B/C <1, то проект(ы) ) не является экономически удовлетворительным

Коэффициент приведенной стоимости

Коэффициент приведенной стоимости (PVR) также может использоваться для экономической оценки проекта(ов) и может быть определен как чистая приведенная стоимость, деленная на чистый отрицательный денежный поток при i*.

Коэффициент приведенной стоимости (PVR) = NPV/PV чистого отрицательного денежного потока 64 Если ПВР=0 тогда проект(ы) находится в экономической безубыточности с другими проектами (с той же ставкой дисконтирования или нормой прибыли)
Если PVR<0, то проект(ы) экономически неудовлетворителен

Пример 3-7

Рассчитайте соотношение B/C и PVR для денежного потока в примере 3-6.