Понятие, формула дисконтирования | Таблица дисконтирования
Знаете ли вы, что означает дисконтирование? Если вы читаете эту статью, значит, вы уже слышали это слово. И если вы пока не поняли до конца, что это такое, то эта статья для вас. Даже если вы не собираетесь сдавать экзамен Дипифр, а просто хотите разобраться в этом вопросе, прочитав эту статью, вы сможете прояснить для себя понятие дисконтирования.
Данная статья доступным языком рассказывает о том, что такое дисконтирование. На простых примерах в ней показана техника расчета дисконтированной стоимости. Вы узнаете, что такое фактор дисконтирования и научитесь пользоваться таблицами коэффициентов дисконтирования.

Понятие и формула дисконтирования доступным языком
Чтобы проще было объяснить понятие дисконтирования, начнём с другого конца. А точнее, возьмем пример из жизни, знакомый каждому.
Пример 1. Представьте, что вы пришли в банк и решили сделать вклад в размере 1000 долларов. Ваши 1000 долларов, положенные в банк сегодня, при банковской ставке 10% будут стоить 1100 долларов завтра: нынешние 1000 долларов + проценты по вкладу 100 (=1000*10%). Итого через год вы сможете снять 1100 долларов. Если выразить этот результат через простую математическую формулу, то получим: $1000*(1+10%) или $1000*(1,10) = $1100.
Через два года нынешние 1000 долларов превратятся в $1210 ($1000 плюс проценты за первый год $100 плюс проценты за второй год $110=1100*10%). Общая формула приращения вклада за два года: (1000*1,10)*1,10 = 1210
С течением времени величина вклада будет расти и дальше. Чтобы узнать, какая сумма вам причитается от банка через год, два и т.д., надо сумму вклада умножить на множитель: (1+R)n
- где R – ставка процента, выраженная в долях от единицы (10% = 0,1)
- N – число лет
В данном примере 1000*(1,10)2 = 1210. Из формулы очевидно (да и из жизни тоже), что сумма вклада через два года зависит от банковской ставки процента. Чем она больше, тем быстрее растет вклад. Если бы ставка банковского процента была другой, например, 12%, то через два года вы бы смогли снять с вклада примерно 1250 долларов, а если считать более точно 1000*(1,12) 2 = 1254.4
Таким способом можно рассчитать величину вашего вклада в любой момент времени в будущем. Расчет будущей стоимости денег в английском языке называется «compounding». Данный термин на русский язык переводят как «наращение» или калькой с английского как «компаундирование». Лично мне больше нравится перевод данного слова как «приращение» или «прирост».
Смысл понятен – с течением времени денежный вклад увеличивается за счет приращения (прироста) ежегодными процентами. На этом, собственно говоря, построена вся банковская система современной (капиталистической) модели мироустройства, в которой время – это деньги.

Теперь давайте посмотрим на данный пример с другого конца. Допустим, вам нужно отдать долг своему приятелю, а именно: через два года заплатить ему $1210. Вместо этого вы можете отдать ему $1000 сегодня, а ваш приятель положит эту сумму в банк под годовую ставку 10% и через два года снимет с банковского вклада ровно необходимую сумму $1210. То есть эти два денежных потока: $1000 сегодня и $1210 через два года —
ПРИМЕР 2. Допустим, через два года вам надо сделать платёж в сумме $1500. Чему эта сумма будет равноценна сегодня?
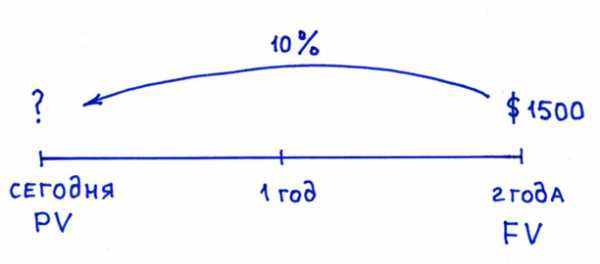 Чтобы рассчитать сегодняшнюю стоимость, нужно идти от обратного: 1500 долларов разделить на (1,10)2 , что будет равно примерно 1240 долларам. Этот процесс и называется дисконтированием.
Чтобы рассчитать сегодняшнюю стоимость, нужно идти от обратного: 1500 долларов разделить на (1,10)2 , что будет равно примерно 1240 долларам. Этот процесс и называется дисконтированием.
Если говорить простым языком, то дисконтирование – это определение сегодняшней стоимости будущей денежной суммы (или если говорить более правильно, будущего денежного потока).
Если вы хотите выяснить, сколько будет стоить сегодня сумма денег, которую вы или получите, или планируете потратить в будущем, то вам надо продисконтировать эту будущую сумму по заданной ставке процента. Эта ставка называется «ставкой дисконтирования». В последнем примере ставка дисконтирования равна 10%, 1500 долларов – это сумма платежа (денежного оттока) через 2 года, а 1240 долларов – это и есть так называемая дисконтированная стоимость будущего денежного потока. В английском языке существуют специальные термины для обозначения сегодняшней (дисконтированной) и будущей стоимости: future value (FV) и present value (PV). В примере выше $1500 — это будущая стоимость FV, а $1240 – это текущая стоимость PV.
Когда мы дисконтируем — мы идём от будущего к сегодняшнему дню.
Дисконтирование
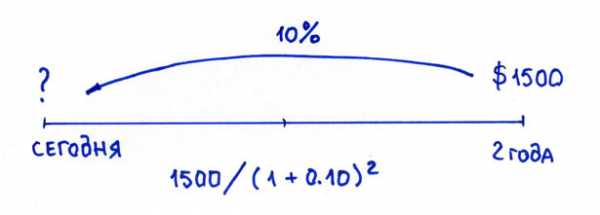
Когда мы наращиваем — мы идём от сегодняшнего дня в будущее.
Наращение
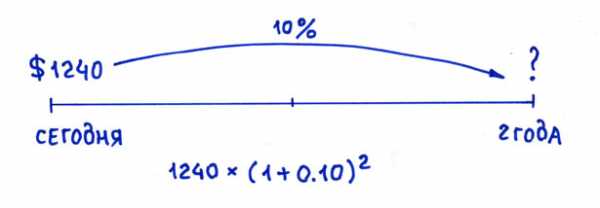
Формула для расчета дисконтированной стоимости или формула дисконтирования для данного примера имеет вид: 1500 * 1/(1+R)n = 1240.
Математическая формула дисконтирования в общем случае будет такая: FV * 1/(1+R)n = PV. Обычно её записывают в таком виде:
PV = FV * 1/(1+R)n
Коэффициент, на который умножается будущая стоимость 1/(1+R)nназывается фактором дисконтирования от английского слова factor в значении «коэффициент, множитель».
В данной формуле дисконтирования: R – ставка процента, N – число лет от даты в будущем до текущего момента.
Таким образом:
- Compounding или Приращение – это, когда вы идете от сегодняшней даты в будущее.
- Discounting или Дисконтирование – это, когда вы идете из будущего к сегодняшнему дню.
Обе «процедуры» позволяют учесть эффект изменения стоимости денег с течением времени.
Конечно, все эти математические формулы сразу наводят тоску на обычного человека, но главное, запомнить суть. Дисконтирование – это когда вы хотите узнать сегодняшнюю стоимость будущей суммы денег (которую вам надо будет потратить или получить).
Надеюсь, что теперь, услышав фразу «понятие дисконтирования», вы сможете объяснить любому, что подразумевается под этим термином.
Приведенная стоимость – это дисконтированная стоимость?
В предыдущем разделе мы выяснили, что
Дисконтирование– это определение текущей стоимости будущих денежных потоков.
Не правда ли, в слове «дисконтирование» слышится слово «дисконт» или по-русски скидка? И действительно, если посмотреть на этимологию слова discount, то уже в 17 веке оно использовалось в значении «deduction for early payment», что означает «скидка за раннюю оплату». Уже тогда много лет назад люди учитывали временную стоимость денег. Таким образом, можно дать еще одно определение: дисконтирование – это расчет скидки за быструю оплату счетов. Эта «скидка» и является мерилом временной стоимости денег или time value of money.
Дисконтированная стоимость – это текущая стоимость будущего денежного потока (т.е. будущий платеж за вычетом «скидки» за быструю оплату). Ее еще называют приведенной стоимостью, от глагола «приводить». Говоря простыми словами, приведенная стоимость – это будущая денежная сумма, приведенная к текущему моменту.
Если быть точным, то дисконтированная и приведенная стоимость – это не абсолютные синонимы. Потому что приводить можно не только будущую стоимость к текущему моменту, но и текущую стоимость к какому-то моменту в будущем. Например, в самом первом примере можно сказать, что 1000 долларов, приведенные к будущему моменту (через два года) при ставке 10% равны 1210 долларов. То есть, я хочу сказать, что приведенная стоимость – это более широкое понятие, чем дисконтированная стоимость.
Кстати, в английском языке такого термина (приведенная стоимость) нет. Это наше, чисто русское изобретение. В английском языке есть термин present value (текущая стоимость) и discounted cash flows (дисконтированные денежные потоки). А у нас есть термин приведенная стоимость, и он чаще всего используется именно в значении «дисконтированная» стоимость.
Таблица дисконтирования
Чуть выше я уже приводила формулу дисконтирования PV = FV * 1/(1+R)n, которую можно описать словами как:
Дисконтированная стоимость равна будущая стоимость, умноженная на некий множитель, который называется фактором дисконтирования.
Коэффициент дисконтирования 1/(1+R)n, как видно из самой формулы, зависит от ставки процента и количества периодов времени. Чтобы не вычислять его каждый раз по формуле дисконтирования, пользуются таблицей, показывающей значения коэффициента в зависимости от % ставки и количества периодов времени. Иногда она называется «таблица дисконтирования», хотя это не совсем правильный термин. Это
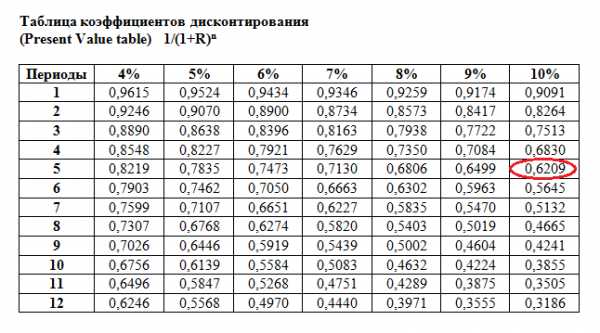
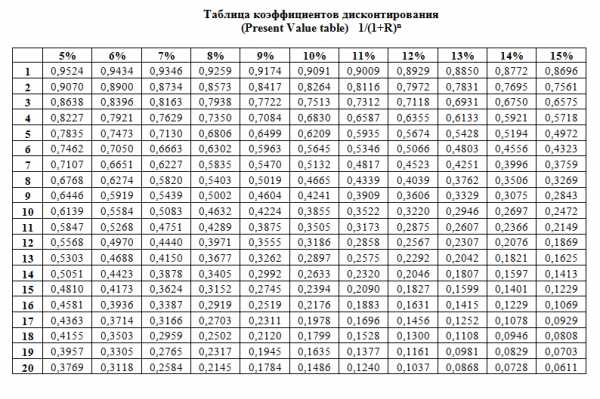
Пользоваться данной таблицей коэффициентов дисконтирования очень просто: если вы знаете ставку дисконтирования и число периодов, например, 10% и 5 лет, то на пересечении соответствующих столбцов находится нужный вам коэффициент.
Пример 3. Давайте разберем простой пример. Допустим, вам нужно выбрать между двумя вариантами:
- А) получить 100,000 долларов сегодня
- Б) или 150,000 долларов одной суммой ровно через 5 лет
Что выбрать?
Если вы знаете, что банковская ставка по 5-летним депозитам составляет 10%, то вы легко можете посчитать, чему равна сумма 150,000 долларов к получению через 5 лет, приведенная к текущему моменту.
Соответствующий коэффициент дисконтирования в таблице равен 0,6209 (ячейка на пересечении строки 5 лет и столбца 10%). 0,6209 означает, что 62,09 цента, полученные сегодня, равны 1 доллару к получению через 5 лет (при ставке 10%). Простая пропорция:
сегодня | через 5 лет |
62,09 цента | $1 |
X? | 150,000 |
Таким образом, $150,000*0,6209 = 93,135.
93,135 — это дисконтированная (приведенная) стоимость суммы $150,000 к получению через 5 лет.
Она меньше, чем 100,000 долларов сегодня. В данном случае, синица в руках действительно лучше, чем журавль в небе. Если мы возьмем 100,000 долларов сегодня, положим их на депозит в банке по 10% годовых, то через 5 лет мы получим: 100,000*1,10*1,10*1,10*1,10*1,10 = 100,000*(1,10)
Чтобы упростить это вычисление (вычисление будущей стоимости при заданной сегодняшней стоимости), можно также воспользоваться таблицей коэффициентов. По аналогии с таблицей дисконтирования эту таблицу можно назвать таблицей коэффициентов приращения (наращения). Вы можете построить такую таблицу самостоятельно в Excele, если используете формулу для расчета коэффициента приращения:(1+R)n.
 Из этой таблицы видно, что 1 доллар сегодня при ставке 10% через 5 лет будет стоить 1,6105 долларов.
Из этой таблицы видно, что 1 доллар сегодня при ставке 10% через 5 лет будет стоить 1,6105 долларов.
С помощью такой таблицы легко будет посчитать, сколько денег нужно положить в банк сегодня, если вы хотите получить определенную сумму в будущем (не пополняя вклад). Чуть более сложная ситуация возникает, когда вы хотите не только положить деньги на депозит сегодня, но и собираетесь каждый год добавлять определенную сумму к своему вкладу. Как это рассчитать, читайте в следующей статье. Она называется формула аннуитета.
Философское отступление для тех, кто дочитал до этого места
Дисконтирование базируется на знаменитом постулате «время — деньги». Если задуматься, то эта иллюстрация имеет очень глубокий смысл. Посадите яблоню сегодня, и через несколько лет ваша яблоня вырастет, и вы будете собирать яблоки в течение многих лет. А если сегодня вы не посадите яблоню, то в будущем яблок вы так и не попробуете.
Всё, что нам нужно – это решиться: посадить дерево, начать свое дело, стать на путь, ведущий к исполнению мечты. Чем раньше мы начнем действовать, тем больший урожай мы получим в конце пути. Нужно превращать время, отпущенное нам в нашей жизни, в результаты.
«Семена цветов, которые распустятся завтра, сажают сегодня». Так говорят китайцы.
Если вы мечтаете о чем-то, не слушайте тех, кто вас отговаривает или подвергает сомнению ваш будущий успех. Не ждите удачного стечения обстоятельств, начинайте как можно раньше. Превращайте время вашей жизни в результаты.
Большая таблица коэффициентов дисконтирования (открывается в новом окне):
Вы можете прочитать другие статьи по теме Финансы:
1. Капитализация вклада — что это? Формула капитализации процентов: ежемесячно, ежедневно, непрерывно.
Рассчитать свой потенциальный доход по вкладу можно самостоятельно, не полагаясь на калькуляторы дохода, которые размещены на сайтах банковских учреждений. В этой статье на конкретных примерах показано, как рассчитать доход по вкладу с капитализацией процентов (ежеквартальной, ежемесячной) и как рассчитать эффективную ставку по вкладам с капитализацией.
2. Формула аннуитета. Вечная рента. Это надо знать каждому! (не для банкиров)
Вечная рента — это серия одинаковых платежей, которые продолжаются вечно. Такой вариант возможен, если, например, у вас есть вклад в банке, вы снимаете только ежегодные проценты, а основная сумма вклада остается нетронутой. Тогда, если ставка процента по вкладу не меняется, у вас будет так называемая вечная рента.
3. Формула расчета NPV инвестиционного проекта. Это просто.
Инвестировать — это значит вложить свободные финансовые ресурсы сегодня с целью получения стабильных денежных потоков в будущем. Как не ошибиться и не только вернуть вложенные средства, но еще и получить прибыль от инвестиций?
4. Внутренняя норма доходности. Формула расчета IRR инвестиционного проекта
В данной статье приведены не только формула и определение IRR, но есть примеры расчетов этого показателя (в Excel, графический) и интерпретации полученных результатов. Два примера из жизни, с которыми сталкивается каждый человек
5. Ставка дисконтирования для инвестиционного проекта. Это WACC — средневзвешенная стоимость капитала.
По своей сути ставка дисконтирования при анализе инвестиционных проектов — это ставка процента, по которой инвестор привлекает финансирование. Как ее рассчитать?
Самые интересные статьи по теме МСФО и Дипифр:
1. Консолидация — это контроль. МСФО IFRS 10 — это единая концепция контроля для любых объединений бизнеса
2. Как сдать экзамен Дипифр со второго раза?
Перейти на главную страницу
msfo-dipifr.ru
Present Value PV — Финансовый словарь смарт-лаб.
PV — Present Value — Текущая стоимость актива.Приведенная к текущему моменту стоимость будущих денежных потоков объекта.
см. также: FV — Future Value
PV и FV связаны простым взаимоотношением:
FV = PV (1 + r) n
PV = FV (1 + r)-n (1)
Пример использования:
Нам известно, что хотим накопить $100 000 в течение 6 лет. Мы знаем, что ставка по депозиту составляет 8% годовых, а значит, можем рассчитать необходимый начальный объем вложений, чтобы получить требуемую выплату:
PV = $100 000/(1 + 1,08)6 = $63 016
Текущая стоимость будущих равномерных платежей (present value of a series of equal cash flow) вычисляется по формуле (2):
Пример задачи:
есть финансовый актив, который будет приносить вам 1000 долларов в год дохода в течение 20 лет начиная через год от текущего момента, при рыночной ставке =12%. Оценить текущую стоимость актива. В этом случае значения можно просто подставлять в формулу.
Если актив начинает приносить доход первый доход 1000 с первого дня его приобретения, то в формулу вместо 20 вставляем 19, и просто к полученному значению прибавляем 1000.
Вычисление present value, когда выплаты начинаются с определенного срока в будущем (Tx).
В этом случае, надо использовать формулу (2) для того чтобы подсчитать PV на момент Tx, а потом вычислить PV на текущий момент по формуле (1), где PV(Tx) станет обычным FV.
Текущая стоимость (present value) суммы регулярных бесконечных денежных потоков вычисляется очень просто:
PV=FV/A
Текущая стоимость неоднородных денежных потоков вычисляется как сумма отдельно взятых дисконтированных доходов:

Измерение FV и PV полезно для сравнения альтернативных способов инвестирования потому что оценка потоков должна быть проведена в одинаковых точках времени — в конце инвест горизонта (FV) или в начале (PV).
smart-lab.ru
Что такое и как рассчитать показатель PV
У многих, кто так или иначе связан с расчетом инвестиций, рано или поздно возникает вопрос: PV – что это такое, и как рассчитать? На самом деле здесь нет ничего сложного, и справиться с такими расчетами может любой желающий.

Прежде всего, PV – это дисконтированная стоимость будущей суммы. Однако, не стоит удивляться, когда вы слышите другие названия: также некоторые её называют текущей или приведенной стоимостью.
Допустим, у нас есть некоторая сумма денег PV, вкладываемая c фиксированной ставкой i в временную единицу t. В качестве временной единицы у нас может выступать что угодно: день и даже год.
То есть, получается, что за каждую временную единицу t зачисляются сверху проценты. Следовательно, в будущем, характеризующимся моментом t. у нас получается сумма FVt, рассчитываемая следующим образом:
FVt=РV(1+i)t
Отсюда можно вывести показатель текущей стоимости РV. Порядок её расчета таков:
РV=FVt(1+i)-t=FVt/(1+i)t
Тогда выходит, что PV – дисконтированная стоимость суммы FVt в будущем, а i – ставка дисконтирования. Такая операция нахождения PV называется дисконтированием.
В итоге, она может быть привязана не только к текущему времени, но и к абсолютно любому моменту времени. Для этого необходимо в знаменателе от индекса t отнять t0.
Предполагается, что есть возможность инвестировать сумму денег в абсолютно любые временные рамки. Например, мы вкладываемся в депозитный счет с показателем доходности i. Однако, при подобном расчете имеет смысл только доход при расчетах риска.
kak1000.ru
Метод расчета чистой текущей стоимости (чистого приведенного эффекта) (net present value — NPV)
Показатель чистой текущей стоимости является производным от показателя текущей стоимости. Под текущей стоимостью (present value — PV) понимается стоимость будущих поступлений денежных средств (future value — FV), отнесенная к настоящему моменту с помощью процедуры дисконтирования. Показатель PV можно рассчитать по формуле, описывающей простую финансовую операцию: размещение денежных средств на условиях срочности, платности, возвратности с единовременным погашением:
PV + r • PV = FV,
где PV — сумма денежных средств, предназначенных для размещения на условиях срочности, платности, возвратности;
r — процентная ставка, являющаяся платой за предоставленные в кредит денежные средства;
FV — сумма погашения кредита, включающая первоначальную сумму долга и проценты.
Преобразование вышеприведенной формулы простой финансовой операции позволит получить формулу расчета показателя текущей стоимости:
PV + r • PV = FV;
PV (1 + r) = FV;
PV= FV / 1+ r = FV 1 / 1 + r;
PV = FV 1 / 1+r.
Если погашение кредита с процентами происходит частями в течение нескольких лет (или частями в течение нескольких лет
поступают доходы от проекта), то формула расчета текущей стоимости будет иметь следующий вид:
Под чистой текущей стоимостью (net present value — NPV) понимается разница между общей суммой дисконтированных потоков будущих поступлений денежных средств, генерируемых данным проектом, и общей суммой инвестиций (invest cost — IС).
где ? FVn — общая сумма будущих поступлений от проекта;
r — доходность проекта;
IС — сумма инвестиций.
Показатель чистой текущей стоимости (NPV) представляет собой разность между совокупными доходами от проекта и совокупными расходами, связанными с проектом. Разность может быть больше нуля, равна нулю или меньше нуля.
Если:
NPV > 0, то проект следует принять;
NPV = 0, то проект является ни прибыльным, ни убыточным;
NPV < 0, то проект следует отвергнуть.
finance-place.ru
Формула FV и PV в Excel — excel
Если вы подсчитаете, что PV делает вручную, формула на самом деле это, для каждого отдельного года:
=Base Amount / (1 + Discount Rate) ^ Periods
Vs, что FV делает вручную, эта формула (которая, как вам кажется, известна, основываясь на следующем ответе в ваших данных):
=Base Amount * (1 - Discount Rate) ^ Periods
Причиной разницы в расчете является математическая разница между двумя пунктами — для фона см. здесь: http://www.investopedia.com/walkthrough/corporate-finance/3/time-value-money/future-value.aspx и здесь: http://www.investopedia.com/walkthrough/corporate-finance/3/time-value-money/present-value-discounting.aspx.
Короче говоря, если у вас сегодня $100 000 и инвестируйте его в то, что дает вам 10% каждый год, то каждый год вы добавляете 10% текущего баланса, чтобы получить новый баланс. т.е.: в 1-м году вы добавляете 100k * 10% = 10k, давая новый итог 110k; в 2-м году вы добавляете 110k * 10% = 11k, давая новое общее количество 121 тыс. и т.д. — Математически количество каждого года определяется по приведенной выше формуле для расчета FV.
Там, где это становится сложно, вы даете себе отрицательную процентную ставку — каждый год ее значение уменьшается на 10%. Вы попытались использовать расчет FV с отрицательной процентной ставкой, но это не совсем правильно. То, что вы должны использовать, — это формула PV.
Для формулы PV, если вы знаете, что каждый год будете получать 100 тыс., вам нужно определить, сколько денег вам нужно было первоначально, чтобы заработать ту же сумму — это текущая стоимость потока денежных потоков, Теперь вам нужно «рассчитать» значение потока дохода каждый год. Формула для этого грубого вычисления выводится математически и приводит к тому, что у меня есть там для PV. Подумайте об этом так: если есть рубашка, которая обычно стоит 100 долларов, а теперь составляет 30%, вы можете увидеть, что вы просто умножаете ее на 30%, чтобы получить 70 долларов. Но если вы видите рубашку на продажу за 70 долларов, а это на 30%, то для определения первоначальной базовой цены вам нужно взять 70 долларов и делить на 0,3, что дает нам 100 долларов.
Чтобы доказать себе, что формула PV подходит, возьмите поток дохода, скажем, 4-го года [3 периода интереса позже, если первый платеж получен в день 0]: 100k/(1 + 10%) ^ 3 = 75 131 долл. США. Теперь работайте в обратном направлении — если вы хотите узнать будущую стоимость инвестиций в размере 75 000 долларов США, рассчитанных на 3 периода, составляющих ежегодно, с годовым коэффициентом 10%, вы идете: 75,131 * (1 + 10%) ^ 3 = 100 тыс.
Это важное финансовое различие, и вы должны прочитать источники, с которыми я связан, чтобы вы поняли это.
qaru.site
Формула FV и PV в Excel
Если подсчитать, что PV делает вручную, формула на самом деле это, для каждого года:
=Base Amount/(1 + Discount Rate)^Periods
Vs, что FV делает вручную, формула этого (что вы, кажется, знаете, на основе придя в тот же ответ в ваших данных):
=Base Amount * (1 - Discount Rate)^Periods
причина для разницы в расчете является математическое различие между двумя элементами — для фона смотрите здесь: http://www.investopedia.com/walkthrough/corporate-finance/3/time-value-money/future-value.aspx и здесь: http://www.investopedia.com/walkthrough/corporate-finance/3/time-value-money/present-value-discounting.aspx.
Короче говоря, если у вас сегодня $ 100 000 и инвестируйте его в то, что дает вам 10% каждый год, то каждый год вы добавляете 10% текущего баланса, чтобы получить новый баланс. т.е.: в 1-м году вы добавляете 100k * 10% = 10k, давая новый итог 110k; в год 2 вы добавляете 110k * 10% = 11k, давая новую сумму в 121 000 и т. д. — Математически количество каждого года определяется по приведенной выше формуле для расчета FV.
Если это сложно, вы даете себе отрицательную процентную ставку — каждый год значение уменьшается на 10%. Вы попытались использовать расчет FV с отрицательной процентной ставкой, но это не совсем правильно. То, что вы должны использовать, — это формула PV.
Для формулы PV, если вы знаете, что вы будете получать 100 тыс. В год, вам необходимо определить, сколько денег вам нужно было первоначально, чтобы заработать ту же сумму — это текущая стоимость денежного потока поток. Теперь вам нужно «рассчитать» значение потока дохода каждого года. Формула для этого грубого вычисления выводится математически и приводит к тому, что у меня есть там для PV. Подумайте об этом — если есть рубашка, которая обычно стоит 100 долларов, а теперь 30%, вы можете увидеть, что вы просто умножаете ее на 30%, чтобы получить 70 долларов.Но если вы видите рубашку в продаже за 70 долларов, а это 30%, то для определения первоначальной базовой цены вам нужно взять $ 70 &. Делитесь на .3 — что дает нам 100 долларов.
Чтобы доказать, что формула PV подходит, возьмите поток дохода, скажем, 4 год [3 периода интереса позже, если первый платеж получен в день 0]: 100 тыс./(1 + 10%)^3 = 75 131. Теперь работайте в обратном направлении — если вы хотите узнать будущую стоимость инвестиций в размере 75 тыс. Долл. США, удерживаемых в течение 3 периодов, составляющих ежегодно с 10% годовой ставкой, вы идете: 75,131 * (1 + 10%)^3 = 100 тыс.
Это важное финансовое различие, и вы должны прочитать источники, с которыми я связан, чтобы вы поняли это.
stackoverrun.com
