Понятие, формула дисконтирования | Таблица дисконтирования
Знаете ли вы, что означает дисконтирование? Если вы читаете эту статью, значит, вы уже слышали это слово. И если вы пока не поняли до конца, что это такое, то эта статья для вас. Даже если вы не собираетесь сдавать экзамен Дипифр, а просто хотите разобраться в этом вопросе, прочитав эту статью, вы сможете прояснить для себя понятие дисконтирования.
Данная статья доступным языком рассказывает о том, что такое дисконтирование. На простых примерах в ней показана техника расчета дисконтированной стоимости. Вы узнаете, что такое фактор дисконтирования и научитесь пользоваться таблицами коэффициентов дисконтирования.
Понятие и формула дисконтирования доступным языком
Чтобы проще было объяснить понятие дисконтирования, начнём с другого конца. А точнее, возьмем пример из жизни, знакомый каждому.
Пример 1. Представьте, что вы пришли в банк и решили сделать вклад в размере 1000 долларов.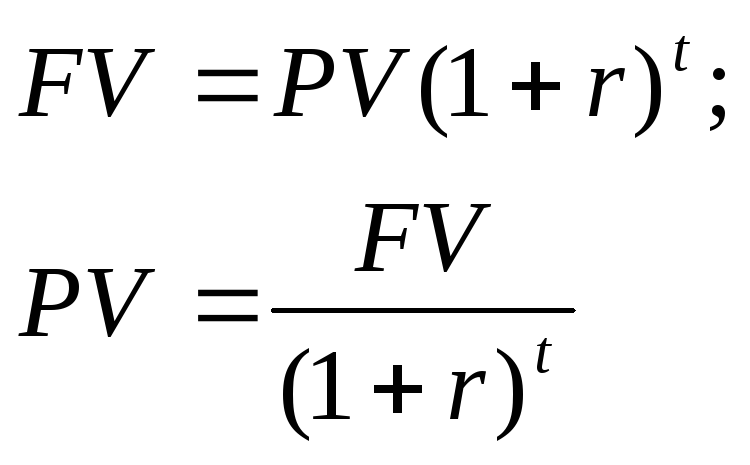
Через два года нынешние 1000 долларов превратятся в $1210 ($1000 плюс проценты за первый год $100 плюс проценты за второй год $110=1100*10%). Общая формула приращения вклада за два года: (1000*1,10)*1,10 = 1210
С течением времени величина вклада будет расти и дальше. Чтобы узнать, какая сумма вам причитается от банка через год, два и т.д., надо сумму вклада умножить на множитель: (1+R)n
- где R – ставка процента, выраженная в долях от единицы (10% = 0,1)
- N – число лет
В данном примере 1000*(1,10)2 = 1210. Из формулы очевидно (да и из жизни тоже), что сумма вклада через два года зависит от банковской ставки процента.
Таким способом можно рассчитать величину вашего вклада в любой момент времени в будущем. Расчет будущей стоимости денег в английском языке называется «compounding». Данный термин на русский язык переводят как «наращение» или калькой с английского как «компаундирование». Лично мне больше нравится перевод данного слова как «приращение» или «прирост».
Смысл понятен – с течением времени денежный вклад увеличивается за счет приращения (прироста) ежегодными процентами. На этом, собственно говоря, построена вся банковская система современной (капиталистической) модели мироустройства, в которой время – это деньги.
Теперь давайте посмотрим на данный пример с другого конца. Допустим, вам нужно отдать долг своему приятелю, а именно: через два года заплатить ему $1210. Вместо этого вы можете отдать ему $1000 сегодня, а ваш приятель положит эту сумму в банк под годовую ставку 10% и через два года снимет с банковского вклада ровно необходимую сумму $1210. То есть эти два денежных потока: $1000 сегодня и $1210 через два года — эквивалентны друг другу. Не важно, что выберет ваш приятель – это две равноценные возможности.
Вместо этого вы можете отдать ему $1000 сегодня, а ваш приятель положит эту сумму в банк под годовую ставку 10% и через два года снимет с банковского вклада ровно необходимую сумму $1210. То есть эти два денежных потока: $1000 сегодня и $1210 через два года — эквивалентны друг другу. Не важно, что выберет ваш приятель – это две равноценные возможности.
ПРИМЕР 2. Допустим, через два года вам надо сделать платёж в сумме $1500. Чему эта сумма будет равноценна сегодня?
Чтобы рассчитать сегодняшнюю стоимость, нужно идти от обратного: 1500 долларов разделить на (1,10)2 , что будет равно примерно 1240 долларам. Этот процесс и называется дисконтированием.
Если говорить простым языком, то дисконтирование – это определение сегодняшней стоимости будущей денежной суммы (или если говорить более правильно, будущего денежного потока).
Если вы хотите выяснить, сколько будет стоить сегодня сумма денег, которую вы или получите, или планируете потратить в будущем, то вам надо продисконтировать эту будущую сумму по заданной ставке процента. Эта ставка называется «ставкой дисконтирования». В последнем примере ставка дисконтирования равна 10%, 1500 долларов – это сумма платежа (денежного оттока) через 2 года, а 1240 долларов – это и есть так называемая дисконтированная стоимость будущего денежного потока. В английском языке существуют специальные термины для обозначения сегодняшней (дисконтированной) и будущей стоимости: future value (FV) и present value (PV). В примере выше $1500 — это будущая стоимость FV, а $1240 – это текущая стоимость PV.
Эта ставка называется «ставкой дисконтирования». В последнем примере ставка дисконтирования равна 10%, 1500 долларов – это сумма платежа (денежного оттока) через 2 года, а 1240 долларов – это и есть так называемая дисконтированная стоимость будущего денежного потока. В английском языке существуют специальные термины для обозначения сегодняшней (дисконтированной) и будущей стоимости: future value (FV) и present value (PV). В примере выше $1500 — это будущая стоимость FV, а $1240 – это текущая стоимость PV.
Когда мы дисконтируем — мы идём от будущего к сегодняшнему дню.
Дисконтирование
Когда мы наращиваем — мы идём от сегодняшнего дня в будущее.
Наращение
Формула для расчета дисконтированной стоимости или формула дисконтирования для данного примера имеет вид: 1500 * 1/(1+R)n = 1240.
Математическая формула дисконтирования в общем случае будет такая: FV * 1/(1+R)n = PV. Обычно её записывают в таком виде:
Обычно её записывают в таком виде:
PV = FV * 1/(1+R)n
Коэффициент, на который умножается будущая стоимость 1/(1+R)nназывается фактором дисконтирования от английского слова factor в значении «коэффициент, множитель».
В данной формуле дисконтирования: R – ставка процента, N – число лет от даты в будущем до текущего момента.
Таким образом:
- Compounding или Приращение – это, когда вы идете от сегодняшней даты в будущее.
- Discounting или Дисконтирование – это, когда вы идете из будущего к сегодняшнему дню.
Обе «процедуры» позволяют учесть эффект изменения стоимости денег с течением времени.
Конечно, все эти математические формулы сразу наводят тоску на обычного человека, но главное, запомнить суть. Дисконтирование – это когда вы хотите узнать сегодняшнюю стоимость будущей суммы денег (которую вам надо будет потратить или получить).
Надеюсь, что теперь, услышав фразу «понятие дисконтирования», вы сможете объяснить любому, что подразумевается под этим термином.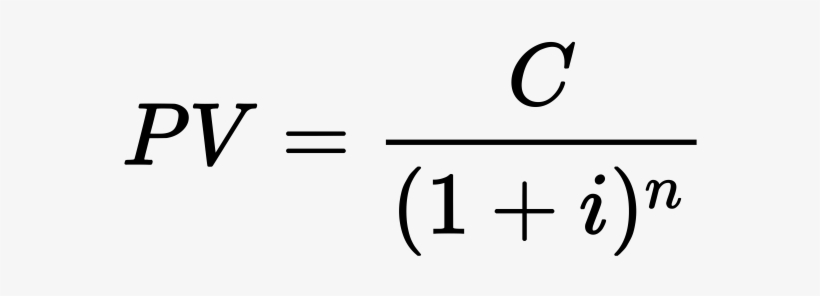
Приведенная стоимость – это дисконтированная стоимость?
В предыдущем разделе мы выяснили, что
Дисконтирование– это определение текущей стоимости будущих денежных потоков.
Не правда ли, в слове «дисконтирование» слышится слово «дисконт» или по-русски скидка? И действительно, если посмотреть на этимологию слова discount, то уже в 17 веке оно использовалось в значении «deduction for early payment», что означает «скидка за раннюю оплату». Уже тогда много лет назад люди учитывали временную стоимость денег. Таким образом, можно дать еще одно определение: дисконтирование – это расчет скидки за быструю оплату счетов. Эта «скидка» и является мерилом временной стоимости денег или time value of money.
Дисконтированная стоимость – это текущая стоимость будущего денежного потока (т.е. будущий платеж за вычетом «скидки» за быструю оплату). Ее еще называют приведенной стоимостью, от глагола «приводить». Говоря простыми словами, приведенная стоимость – это будущая денежная сумма, приведенная к текущему моменту.
Если быть точным, то дисконтированная и приведенная стоимость – это не абсолютные синонимы. Потому что приводить можно не только будущую стоимость к текущему моменту, но и текущую стоимость к какому-то моменту в будущем. Например, в самом первом примере можно сказать, что 1000 долларов, приведенные к будущему моменту (через два года) при ставке 10% равны 1210 долларов. То есть, я хочу сказать, что приведенная стоимость – это более широкое понятие, чем дисконтированная стоимость.
Кстати, в английском языке такого термина (приведенная стоимость) нет. Это наше, чисто русское изобретение. В английском языке есть термин present value (текущая стоимость) и discounted cash flows (дисконтированные денежные потоки). А у нас есть термин приведенная стоимость, и он чаще всего используется именно в значении «дисконтированная» стоимость.
Таблица дисконтирования
Чуть выше я уже приводила формулу дисконтирования PV = FV * 1/(1+R)n, которую можно описать словами как:
Дисконтированная стоимость равна будущая стоимость, умноженная на некий множитель, который называется фактором дисконтирования.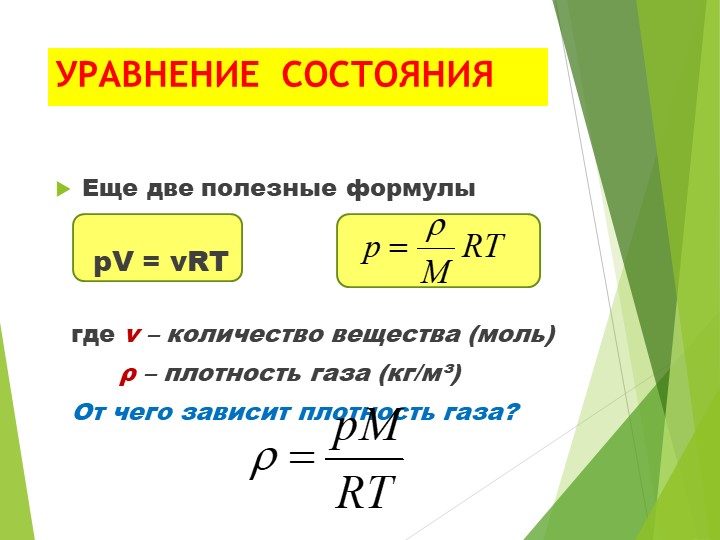
Коэффициент дисконтирования 1/(1+R)n, как видно из самой формулы, зависит от ставки процента и количества периодов времени. Чтобы не вычислять его каждый раз по формуле дисконтирования, пользуются таблицей, показывающей значения коэффициента в зависимости от % ставки и количества периодов времени. Иногда она называется «таблица дисконтирования», хотя это не совсем правильный термин. Это таблица коэффициентов дисконтирования, которые рассчитываются, как правило, с точностью до четвертого знака после запятой.
Пользоваться данной таблицей коэффициентов дисконтирования очень просто: если вы знаете ставку дисконтирования и число периодов, например, 10% и 5 лет, то на пересечении соответствующих столбцов находится нужный вам коэффициент.
Пример 3. Давайте разберем простой пример. Допустим, вам нужно выбрать между двумя вариантами:
- А) получить 100,000 долларов сегодня
- Б) или 150,000 долларов одной суммой ровно через 5 лет
Что выбрать?
Если вы знаете, что банковская ставка по 5-летним депозитам составляет 10%, то вы легко можете посчитать, чему равна сумма 150,000 долларов к получению через 5 лет, приведенная к текущему моменту.
Соответствующий коэффициент дисконтирования в таблице равен 0,6209 (ячейка на пересечении строки 5 лет и столбца 10%). 0,6209 означает, что 62,09 цента, полученные сегодня, равны 1 доллару к получению через 5 лет (при ставке 10%). Простая пропорция:
сегодня | через 5 лет |
62,09 цента | $1 |
X? | 150,000 |
Таким образом, $150,000*0,6209 = 93,135.
93,135 — это дисконтированная (приведенная) стоимость суммы $150,000 к получению через 5 лет.
Она меньше, чем 100,000 долларов сегодня. В данном случае, синица в руках действительно лучше, чем журавль в небе. Если мы возьмем 100,000 долларов сегодня, положим их на депозит в банке по 10% годовых, то через 5 лет мы получим: 100,000*1,10*1,10*1,10*1,10*1,10 = 100,000*(1,10)5 = 161,050 долларов. Это более выгодный вариант.
Это более выгодный вариант.
Чтобы упростить это вычисление (вычисление будущей стоимости при заданной сегодняшней стоимости), можно также воспользоваться таблицей коэффициентов. По аналогии с таблицей дисконтирования эту таблицу можно назвать таблицей коэффициентов приращения (наращения). Вы можете построить такую таблицу самостоятельно в Excele, если используете формулу для расчета коэффициента приращения:(1+R)n.
Из этой таблицы видно, что 1 доллар сегодня при ставке 10% через 5 лет будет стоить 1,6105 долларов.
С помощью такой таблицы легко будет посчитать, сколько денег нужно положить в банк сегодня, если вы хотите получить определенную сумму в будущем (не пополняя вклад). Чуть более сложная ситуация возникает, когда вы хотите не только положить деньги на депозит сегодня, но и собираетесь каждый год добавлять определенную сумму к своему вкладу. Как это рассчитать, читайте в следующей статье. Она называется формула аннуитета.
Философское отступление для тех, кто дочитал до этого места
Дисконтирование базируется на знаменитом постулате «время — деньги». Если задуматься, то эта иллюстрация имеет очень глубокий смысл. Посадите яблоню сегодня, и через несколько лет ваша яблоня вырастет, и вы будете собирать яблоки в течение многих лет. А если сегодня вы не посадите яблоню, то в будущем яблок вы так и не попробуете.
Если задуматься, то эта иллюстрация имеет очень глубокий смысл. Посадите яблоню сегодня, и через несколько лет ваша яблоня вырастет, и вы будете собирать яблоки в течение многих лет. А если сегодня вы не посадите яблоню, то в будущем яблок вы так и не попробуете.
Всё, что нам нужно – это решиться: посадить дерево, начать свое дело, стать на путь, ведущий к исполнению мечты. Чем раньше мы начнем действовать, тем больший урожай мы получим в конце пути. Нужно превращать время, отпущенное нам в нашей жизни, в результаты.
«Семена цветов, которые распустятся завтра, сажают сегодня». Так говорят китайцы.
Если вы мечтаете о чем-то, не слушайте тех, кто вас отговаривает или подвергает сомнению ваш будущий успех. Не ждите удачного стечения обстоятельств, начинайте как можно раньше. Превращайте время вашей жизни в результаты.
Большая таблица коэффициентов дисконтирования (открывается в новом окне):
Вы можете прочитать другие статьи по теме Финансы:
1. Капитализация вклада — что это? Формула капитализации процентов: ежемесячно, ежедневно, непрерывно.
Капитализация вклада — что это? Формула капитализации процентов: ежемесячно, ежедневно, непрерывно.
Рассчитать свой потенциальный доход по вкладу можно самостоятельно, не полагаясь на калькуляторы дохода, которые размещены на сайтах банковских учреждений. В этой статье на конкретных примерах показано, как рассчитать доход по вкладу с капитализацией процентов (ежеквартальной, ежемесячной) и как рассчитать эффективную ставку по вкладам с капитализацией.
2. Формула аннуитета. Вечная рента. Это надо знать каждому! (не для банкиров)
Вечная рента — это серия одинаковых платежей, которые продолжаются вечно. Такой вариант возможен, если, например, у вас есть вклад в банке, вы снимаете только ежегодные проценты, а основная сумма вклада остается нетронутой. Тогда, если ставка процента по вкладу не меняется, у вас будет так называемая вечная рента.
3. Формула расчета NPV инвестиционного проекта. Это просто.
Инвестировать — это значит вложить свободные финансовые ресурсы сегодня с целью получения стабильных денежных потоков в будущем. Как не ошибиться и не только вернуть вложенные средства, но еще и получить прибыль от инвестиций?
Как не ошибиться и не только вернуть вложенные средства, но еще и получить прибыль от инвестиций?
4. Внутренняя норма доходности. Формула расчета IRR инвестиционного проекта
В данной статье приведены не только формула и определение IRR, но есть примеры расчетов этого показателя (в Excel, графический) и интерпретации полученных результатов. Два примера из жизни, с которыми сталкивается каждый человек
5. Ставка дисконтирования для инвестиционного проекта. Это WACC — средневзвешенная стоимость капитала.
По своей сути ставка дисконтирования при анализе инвестиционных проектов — это ставка процента, по которой инвестор привлекает финансирование. Как ее рассчитать?
Самые интересные статьи по теме МСФО и Дипифр:
1. Консолидация — это контроль. МСФО IFRS 10 — это единая концепция контроля для любых объединений бизнеса
2. Как сдать экзамен Дипифр со второго раза?
Перейти на главную страницу
Функция ПС (PV) — Справочник
Обязательный. Процентная ставка за период.
Процентная ставка за период.
Например, если получен кредит на автомобиль под 10 процентов годовых и выплаты производятся ежемесячно, процентная ставка за месяц составит 10%/12 (0,83%). В качестве значения аргумента «ставка» нужно ввести в формулу 10%/12, 0,83% или 0,0083.
Обязательный. Общее число периодов платежей для ежегодного платежа.
Например, если получен кредит на 4 года на покупку автомобиля и платежи производятся ежемесячно, то кредит имеет 4*12 (или 48) периодов. В качестве значения аргумента «кпер» в формулу нужно ввести число 48.
Обязательный. Выплата, производимая в каждый период и не меняющаяся на протяжении всего периода ежегодного платежа. Обычно аргумент «плт» состоит из выплат в счет основной суммы и платежей по процентам, но не включает в себя другие сборы или налоги.
Например, ежемесячная выплата по кредиту в размере 10 000 р. под 12 процентов годовых на 4 года составит 263,33р. В качестве значения аргумента «плт» нужно ввести в формулу число -263,33. Если он опущен, аргумент «бс» является обязательным.
Если он опущен, аргумент «бс» является обязательным.
Необязательный. Значение будущей стоимости, т. е. желаемого остатка средств после последнего платежа. Если аргумент «бс» опущен, предполагается, что он равен 0 (например, будущая стоимость для займа равна 0).
Предположим, что для определенной цели требуется накопить 50 000 р. за 18 лет: в этом случае будущая стоимость равна 50 000 р. Предположив, что заданная процентная ставка останется без изменений, можно определить, какую сумму необходимо откладывать каждый месяц. Если аргумент «бс» опущен, необходимо использовать аргумент «плт».
| Тип | Когда нужно платить |
|---|---|
| 0 или опущен | В конце периода |
| 1 | В начале периода |
Функция PV
Возвращает значение типа double, указывающее текущее значение ежегодного платежа на основе периодических фиксированных будущих выплат и фиксированной процентной ставки.
Синтаксис
ПС( ставка; кпер ;плт [; бс]; [; тип] )
Функция ПС имеет следующие аргументы:
|
Аргумент |
Описание |
|
ставка |
Обязательный аргумент. |
|
кпер |
Обязательный аргумент. Целое число, указывающее общее количество периодов оплаты. Например, при ежемесячных выплатах по четырехгодичному кредиту на машину число периодов выплат равно 4*12 (или 48). |
|
плт |
Обязательный аргумент. Значение double, обозначающее платеж, который должен выплачиваться в каждый период. |
|
бс |
Необязательный аргумент. Вариант, обозначающий будущую стоимость или баланс, которые вы хотите достичь после последней выплаты. Например, будущая стоимость для займа равна 0 р., поскольку это значение останется после последней выплаты. Но если вы хотите накопить за 18 лет 50 000 $ на образование ребенка, будущая стоимость равна 50 000 $. Если этот аргумент не задан, используется значение 0. |
|
тип |
Необязательный аргумент. |
Замечания
Выплатами называется ряд фиксированных платежей наличными, которые выполняются в определенный период времени. Это может быть заём (например, ипотека) или инвестиция (например, сберегательный вклад с ежемесячным пополнением).
При вычислении значений ставка и кпер нужно использовать периоды оплаты, выраженные в одних и тех же единицах. Например, если ставка вычисляется с использованием месяцев, значение кпер также должно рассчитываться с использованием месяцев.
Все аргументы, которым соответствуют выплачиваемые денежные средства (например, сберегательные вклады), представляются отрицательными числами, а получаемые (например, дивиденды) — положительными.
Пример запроса
|
Выражение |
Результаты: |
|
SELECT FinancialSample.*, ПС([AnnualRate]/12,[TermInYears]*12,-[MonthlyRePayment],0,0) AS PresentValue FROM FinancialSample; |
Возвращает все поля из таблицы FinancialSample, вычисляет стоимость аннуитета на основе годового ящика, «MonthlyRePayment» и «TermInYears» и отображает результаты в столбце PresentValue. |
Пример VBA
Примечание: В примерах ниже показано, как использовать эту функцию в модуле Visual Basic для приложений (VBA). Чтобы получить дополнительные сведения о работе с VBA, выберите Справочник разработчика в раскрывающемся списке рядом с полем Поиск и введите одно или несколько слов в поле поиска.
Чтобы получить дополнительные сведения о работе с VBA, выберите Справочник разработчика в раскрывающемся списке рядом с полем Поиск и введите одно или несколько слов в поле поиска.
В этом примере функция Пс возвращает текущую стоимость выплаты в размере 1 млн р., которая будет обеспечивать 50 000 р. в год в течение следующих 20 лет. Указаны ожидаемая годовая процентная ставка (APR), общее число платежей (TotPmts), размер каждого платежа (YrIncome), общая будущая стоимость инвестиции (FVal) и число, которое показывает, когда делается платеж — в начале или в конце периода оплаты (PayType). Обратите внимание на то, что число YrIncome отрицательное, так как оно представляет собой средства, выплачиваемые каждый год.
Dim Fmt, APR, TotPmts, YrIncome, FVal, PayType, PVal
Const ENDPERIOD = 0, BEGINPERIOD = 1
Fmt = "###,##0.00" ' Define money format.
APR = .0825 ' Annual percentage rate.
TotPmts = 20 ' Total number of payments.
YrIncome = 50000 ' Yearly income.
FVal = 1000000 ' Future value.
PayType = BEGINPERIOD ' Payment at beginning of month.
PVal = PV(APR, TotPmts, -YrIncome, FVal, PayType)
MsgBox "The present value is " & Format(PVal, Fmt) & "."
3. Методика расчета приведенной стоимости денежных потоков / КонсультантПлюс
3. Методика расчета
приведенной стоимости денежных потоков
Расчет величины приведенной стоимости PV будущего денежного потока периодичных выплат CFt на момент времени t0 производится на основе формулы для исчисления сложных процентов, исходя из того, что сумма начисленного за процентный период процентного дохода капитализируется (добавляется к сумме вклада и в следующем процентном периоде также приносит доход):
При совпадении момента приведения t0 с началом первого процентного периода и момента выплаты tn с окончанием n-го процентного периода справедлива формула:
где i — норма дисконта за процентный период, %;
n — количество процентных периодов до выплаты.
Для графика периодичных выплат их приведенная стоимость рассчитывается следующим образом:
где CFn — сумма выплаты с порядковым номером n;
N — количество выплат по графику после момента приведения t0.
В случае, если в течение года предусмотрено несколько процентных выплат (в году имеется несколько процентных периодов), при использовании формулы (1) применяется норма дисконта, рассчитываемая по следующей формуле:
m — количество процентных периодов в году.
В случае, если дата, на которую производится расчет приведенной стоимости выплат, не совпадает с началом первого полного процентного периода, каждое слагаемое ряда в формуле (1) дополнительно дисконтируется путем умножения его на коэффициент , где T — временной интервал (в днях) между моментом приведения t0 и датой ближайшей выплаты по графику.
Просроченная задолженность не дисконтируется.
Таким образом, формула для расчета приведенной стоимости выплат будет выглядеть следующим образом:
где D — сумма просроченной задолженности.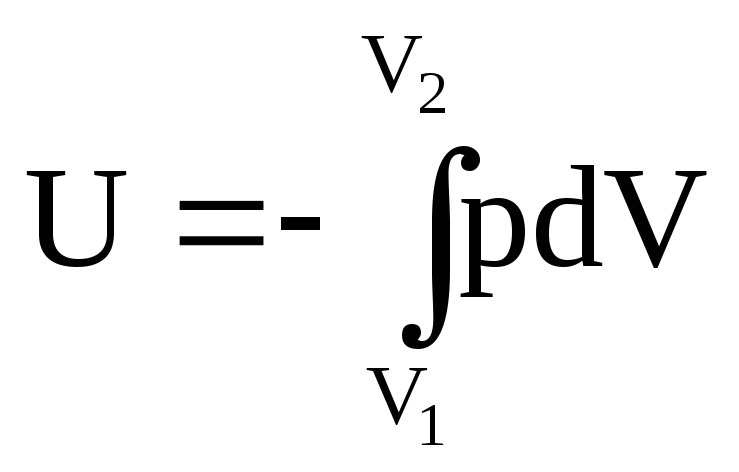
4. Расчет номинальной стоимости пакета Долговых инструментов, эквивалентного по приведенной стоимости номинальной сумме погашаемой Задолженности заемщика.
В качестве момента приведения t0 принимается первое число месяца, в котором заключается соответствующее соглашение о погашении Задолженности заемщика.
Расчет приведенной стоимости будущих выплат по каждому Долговому инструменту (далее обозначается PV0) производится по формуле (2) на основании графика, установленного условиями эмиссии и обращения Долгового инструмента.
Расчет приведенной стоимости будущих погашаемых выплат по обязательствам заемщика (далее обозначается PVК) производится по формуле (2) на основании графика погашения Задолженности заемщика, установленного условиями соответствующего соглашения (договора).
Расчет номинальной стоимости пакета Долговых инструментов (далее обозначается NБ), эквивалентного по приведенной стоимости номинальной сумме погашаемой Задолженности заемщика, производится по формуле:
PVК — приведенная стоимость погашаемой Задолженности заемщика;
N0 — номинальная сумма пакета Долговых инструментов, используемого для расчета приведенной стоимости выплат по нему;
PV0 — приведенная стоимость выплат по пакету Долговых инструментов номинальной стоимостью N0 на момент приведения t0.
Открыть полный текст документа
Метод расчета чистой текущей стоимости (чистого приведенного эффекта) (net present value — NPV)
Показатель чистой текущей стоимости является производным от показателя текущей стоимости. Под текущей стоимостью (present value — PV) понимается стоимость будущих поступлений денежных средств (future value — FV), отнесенная к настоящему моменту с помощью процедуры дисконтирования. Показатель PV можно рассчитать по формуле, описывающей простую финансовую операцию: размещение денежных средств на условиях срочности, платности, возвратности с единовременным погашением:
PV + r • PV = FV,
где PV — сумма денежных средств, предназначенных для размещения на условиях срочности, платности, возвратности;
r — процентная ставка, являющаяся платой за предоставленные в кредит денежные средства;
FV — сумма погашения кредита, включающая первоначальную сумму долга и проценты.
Преобразование вышеприведенной формулы простой финансовой операции позволит получить формулу расчета показателя текущей стоимости:
PV + r • PV = FV;
PV (1 + r) = FV;
PV= FV / 1+ r = FV 1 / 1 + r;
PV = FV 1 / 1+r.
Если погашение кредита с процентами происходит частями в течение нескольких лет (или частями в течение нескольких лет
поступают доходы от проекта), то формула расчета текущей стоимости будет иметь следующий вид:
Под чистой текущей стоимостью (net present value — NPV) понимается разница между общей суммой дисконтированных потоков будущих поступлений денежных средств, генерируемых данным проектом, и общей суммой инвестиций (invest cost — IС).
где ? FVn — общая сумма будущих поступлений от проекта;
r — доходность проекта;
IС — сумма инвестиций.
Показатель чистой текущей стоимости (NPV) представляет собой разность между совокупными доходами от проекта и совокупными расходами, связанными с проектом. Разность может быть больше нуля, равна нулю или меньше нуля.
Если:
NPV > 0, то проект следует принять;
NPV = 0, то проект является ни прибыльным, ни убыточным;
NPV < 0, то проект следует отвергнуть.
Формула текущей стоимости | Калькулятор (Примеры с шаблоном Excel)
Формула приведенной стоимости (Содержание)
- формула
- Примеры
- Калькулятор
Что такое формула текущей стоимости?
Термин «текущая стоимость» относится к применению временной стоимости денег, которая дисконтирует будущий денежный поток для достижения его текущей стоимости. Ставка дисконтирования, используемая для текущей стоимости, определяется на основе текущей рыночной доходности. Формула для приведенной стоимости может быть получена путем дисконтирования будущего денежного потока с использованием предварительно определенной ставки (ставки дисконтирования) и количества лет.
Формула для PV приведена ниже:
PV = CF / (1 + r) t
Где,
- PV = текущая стоимость
- CF = будущий денежный поток
- r = ставка дисконтирования
- t = количество лет
В случае нескольких рецептур в год (обозначается как n) формула для PV может быть расширена как
PV = CF / (1 + r/n) t*n
Давайте рассмотрим пример, чтобы лучше понять расчет приведенной стоимости.
Формула текущей стоимости — пример № 1
Давайте рассмотрим простой пример будущего денежного потока в 2000 долларов, который будет получен через 3 года. В соответствии с текущей тенденцией рынка применяемая ставка дисконтирования составляет 4%. Рассчитайте стоимость будущего денежного потока сегодня.
Решение:
Приведенная стоимость рассчитывается по формуле, приведенной ниже
PV = CF / (1 + r) т
- Приведенная стоимость = 2 000 долл. США / (1 + 4%) 3
- Текущая стоимость = 1 777, 99 $
Таким образом, денежный поток в 2000 долларов, который будет получен через 3 года, сегодня стоит 1777, 99 долларов .
Формула текущей стоимости — пример № 2
Давайте возьмем пример Давида, который сегодня ищет определенную сумму денег, чтобы через 4 года он мог снять 3000 долларов. Применяемая ставка дисконтирования составляет 5% и будет составляться раз в полгода. Подсчитайте сумму, которую Дэвид должен внести сегодня.
Применяемая ставка дисконтирования составляет 5% и будет составляться раз в полгода. Подсчитайте сумму, которую Дэвид должен внести сегодня.
Решение:
Приведенная стоимость рассчитывается по формуле, приведенной ниже
PV = CF / (1 + r / n) t * n
- Текущая стоимость = 3000 долл. США / (1 + 5% / 2) 4 * 2
- Приведенная стоимость = $ 2462, 24
Таким образом, Дэвид обязан внести 2462 доллара сегодня, чтобы он мог снять 3000 долларов через 4 года.
Формула текущей стоимости — пример № 3
Давайте возьмем другой пример Джона, который выиграл в лотерею и согласно ее условиям, он имеет право на ежегодную выплату наличными в размере 1000 долларов США в течение следующих 4 лет. Учетная ставка составляет 4%. Рассчитайте текущую стоимость всех будущих денежных потоков, начиная с конца текущего года.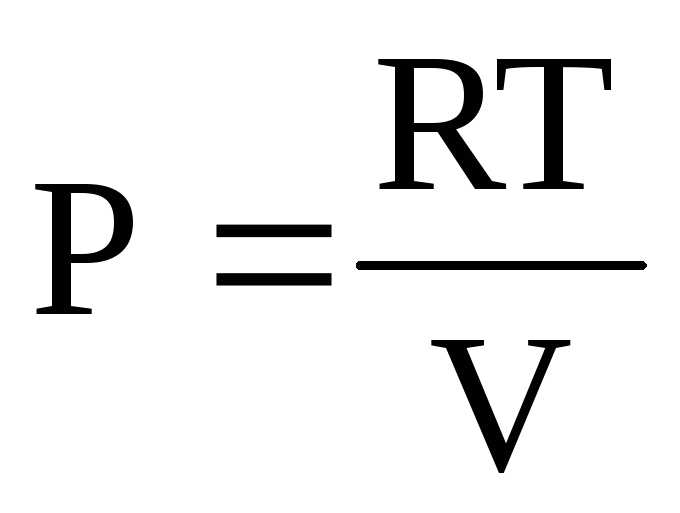
Решение:
Приведенная стоимость рассчитывается по формуле, приведенной ниже
PV = CF / (1 + r) т
На 1- й год,
- Текущая стоимость = 1 000 долл. / (1 + 4%) 1
- Текущая стоимость = $ 961, 54
На 2- й год,
- Текущая стоимость = 1000 долл. США / (1 + 4%) 2
- Текущая стоимость = $ 924, 56
За 3- й год,
- Текущая стоимость = 1000 долл. США / (1 + 4%) 3
- Текущая стоимость = $ 889, 00
За 4- й год,
- Текущая стоимость = 1000 долл. США / (1 + 4%) 4
- Текущая стоимость = 854.80 $
Приведенная стоимость за весь год рассчитывается как:
- Приведенная стоимость = $ 961, 54 + $ 924, 56 + $ 889, 00 + $ 854, 80
- Приведенная стоимость = $ 3 629, 90
Таким образом, нынешняя стоимость выигрыша Джона в лотерею составляет $ 3629, 90 .
объяснение
Формула для приведенной стоимости может быть получена с помощью следующих шагов:
Шаг 1: Во-первых, выясните будущий денежный поток, который обозначается CF.
Шаг 2: Затем определите ставку дисконтирования на основе текущей рыночной доходности. Это скорость дисконтирования будущих денежных потоков, и она обозначается как r.
Шаг 3: Затем определите количество лет, пока не начнется будущий денежный поток, и обозначим его как t.
Шаг 4: Наконец, формула для приведенной стоимости может быть получена путем дисконтирования будущего денежного потока (шаг 1) с использованием ставки дисконтирования (шаг 2) и количества лет (шаг 3), как показано ниже.
PV = CF / (1 + r) т
Шаг 5: Далее, если известно количество рецептур в год (n), тогда формула для приведенной стоимости может быть выражена как
PV = CF / (1 + r / n) t * n
Актуальность и использование формулы приведенной стоимости
Концепция текущей стоимости в основном основана на временной стоимости денег, в которой говорится, что доллар сегодня стоит больше доллара в будущем.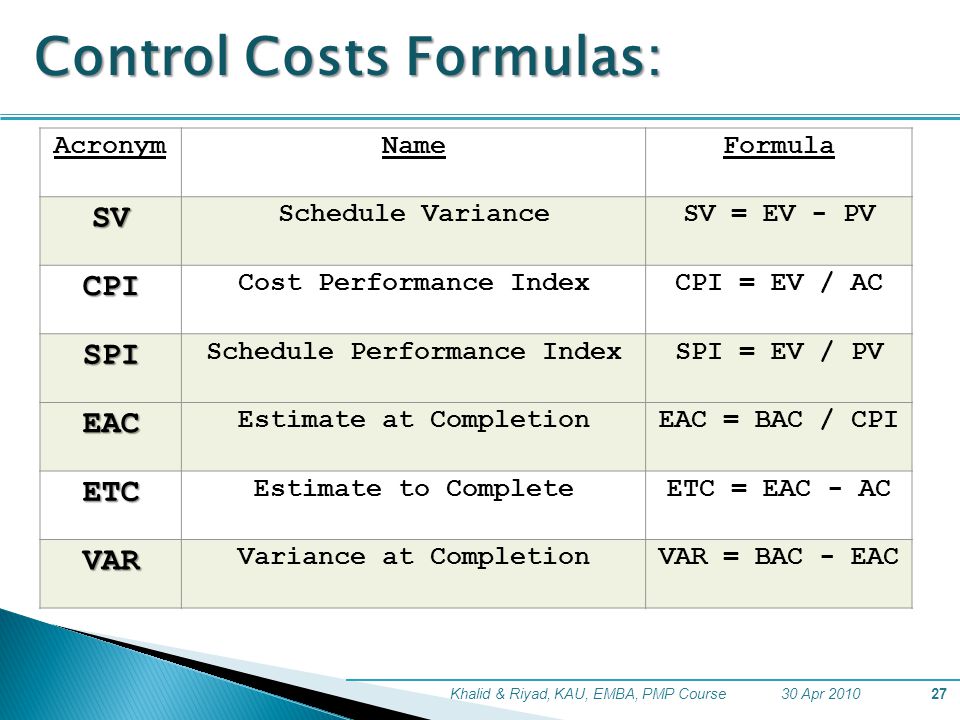 Однако существует ограничение расчета приведенной стоимости, поскольку предполагается, что одна и та же норма прибыли будет получена в течение всего периода времени — ни одна инвестиция не может гарантировать норму прибыли, поскольку различные рыночные факторы могут негативно влиять на норму прибыли. в результате эрозии текущей стоимости. Таким образом, допущение соответствующей ставки дисконтирования тем более важно для правильной оценки будущих денежных потоков.
Однако существует ограничение расчета приведенной стоимости, поскольку предполагается, что одна и та же норма прибыли будет получена в течение всего периода времени — ни одна инвестиция не может гарантировать норму прибыли, поскольку различные рыночные факторы могут негативно влиять на норму прибыли. в результате эрозии текущей стоимости. Таким образом, допущение соответствующей ставки дисконтирования тем более важно для правильной оценки будущих денежных потоков.
Калькулятор формулы приведенной стоимости
Вы можете использовать следующий калькулятор текущей стоимости
| PV = |
| |||||||||
|
Рекомендуемые статьи
Это было руководство к формуле текущей стоимости. Здесь мы обсуждаем, как рассчитать приведенную стоимость вместе с практическими примерами. Мы также предоставляем калькулятор текущей стоимости с загружаемым шаблоном Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше —
Здесь мы обсуждаем, как рассчитать приведенную стоимость вместе с практическими примерами. Мы также предоставляем калькулятор текущей стоимости с загружаемым шаблоном Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше —
- Руководство по формуле фактора текущей стоимости
- Примеры формулы анализа отклонений
- Как рассчитать стандартное отклонение образца?
- Формула дисперсии населения с шаблоном Excel
Total PV SH 100
Total PV SH 100 —
высококачественное полусинтетическое масло для вакуумных насосов, работающих в пищевой промышленности..
Применение.
Масло специально разработано для насосов, которые перекачивают кислотные или коррозионно-агрессивные газы.
Total PV SH 100 рекомендуется использовать для вакуумных насосов с возвратно-поступательным ходом поршня или ротационных вакуумных насосов.
Спецификации
Формула масла Total PV SH 100 содержит ингредиенты, соответствующие требованиям United States FDA (управление по
контролю за продуктами и лекарствами США) 21 CFR 178. 3570.
3570.
Пищевой допуск NSF класс H-1, для случайного контакта с пищевыми продуктами.
Регистрационный номер NSF 134 951
Преимущества.
• Total PV SH 100 характеризуется отличной смазывающей способностью и высокой стойкостью к воздействию химических реагентов.
• Хорошо поддерживает низкое давления насыщенных паров, что особенно важно для получение требуемого вакуума.
• Отлично противостоит образованию отложений, защищает оборудование от разрушения и старения.
|
Калькулятор текущей стоимости
Использование калькулятора
Найдите текущую стоимость будущей денежной суммы. Калькулятор приведенной стоимости отвечает на вопрос: «Что мне нужно инвестировать сегодня, чтобы иметь определенную сумму денег в будущем?»
Калькулятор приведенной стоимости отвечает на вопрос: «Что мне нужно инвестировать сегодня, чтобы иметь определенную сумму денег в будущем?»
Вы можете думать о приведенной стоимости как о сумме, которую вам нужно откладывать сейчас, чтобы иметь определенную сумму денег в будущем. Формула приведенной стоимости применяет дисконт к вашей будущей сумме стоимости, вычитая заработанные проценты, чтобы найти текущую стоимость в сегодняшних деньгах.
Формула и калькулятор текущей стоимости
Формула приведенной стоимости: PV = FV / (1 + i) n , где вы делите будущую стоимость FV на коэффициент 1 + i для каждого периода между настоящей и будущей датами.
Введите эти числа в калькулятор текущей стоимости для расчета PV:
- Сумма будущей стоимости FV
- Количество временных периодов (лет) t , что составляет n в формуле
- Процентная ставка R , что составляет i в формуле
- Частота компаундирования
- Денежный поток исходящих платежей
- Темп прироста аннуитета
Приведенная стоимость денежной суммы будет стоить больше в будущем, когда она инвестируется и приносит проценты.
Текущая стоимость — это сумма, которую вам нужно будет инвестировать сейчас с известной процентной ставкой и ставкой сложных процентов, чтобы у вас была определенная сумма денег в определенный момент в будущем.
Вы можете ввести 0 для любой переменной, которую хотите исключить при использовании этого калькулятора. Другой наш Калькуляторы приведенной стоимости предлагают более специализированные вычисления приведенной стоимости.
Что входит в расчет текущей стоимости
Калькулятор приведенной стоимости использует следующее, чтобы найти приведенную стоимость PV будущей суммы плюс проценты минус выплаты денежного потока:
- Будущая стоимость FV
- Будущая стоимость денежной суммы
- Кол-во временных периодов т
- • Периоды времени обычно составляют несколько лет.

• Убедитесь, что все ваши входные данные используют одну и ту же единицу периода времени (годы, месяцы и т. Д.))
• Введите p или бессрочный для бессрочного аннуитета - Процентная ставка R
- Номинальная процентная ставка или заявленная ставка в процентах
- Компаундирование м
- • Количество начислений сложных процентов за период
• Введите 1 для годового начисления сложных процентов, то есть один раз в год.
• Введите 4 для ежеквартального начисления сложных процентов.
• Введите 12 для ежемесячного начисления сложных процентов.
• Введите 365 для ежедневного начисления сложных процентов
• Введите c или непрерывный для непрерывного компаундирования.
- Отправление аннуитетных платежей денежного потока PMT
- Сумма платежа за каждый период
- Скорость роста G
- Темп роста аннуитетных платежей за период, введенный в процентах
- Количество платежей q за период
- • Частота выплат
• Введите 1 для годовых платежей, которые производятся один раз в год.
• Введите 4 для ежеквартальных платежей.
• Введите 12 для ежемесячных платежей.
• Введите 365 для ежедневных платежей - Когда происходят аннуитетные выплаты T
- • Выберите конец , который является обычным аннуитетом для платежей в конце периода.

• Выберите начало для платежей в начале периода - Текущая стоимость PV
- Результатом расчета PV является приведенная стоимость любой будущей суммы стоимости плюс будущие денежные потоки или аннуитетные выплаты
В разделах ниже показано, как получить формулы приведенной стоимости.Список представленных здесь формул см. На нашей странице формул приведенной стоимости.
Вывод формулы приведенной стоимости
Будущая стоимость ( FV ) суммы приведенной стоимости ( PV ), на которую накапливаются проценты по ставке i за один период времени, представляет собой текущую стоимость плюс проценты, заработанные на этой сумме. Математическое уравнение
\ (FV = PV + PVi \)
или
\ (FV = PV (1 + i) \)
Для каждого периода в будущем накопленная стоимость увеличивается на дополнительный коэффициент (1 + i). 4} +.n \ right] (1 + iT) \ tag {3} \)
4} +.n \ right] (1 + iT) \ tag {3} \)
Приведенная стоимость растущей ренты (g = i)
Если g = i, вы заметите, что члены (1 + g) сокращаются в уравнении (3a), и мы получаем
\ (PV = \ dfrac {PMT} {(1 + i)} + \ dfrac {PMT} {(1 + i)} + \ dfrac {PMT} {(1 + i)} + … + \ dfrac {PMT} {(1 + i)} \)
, так как теперь у нас есть n экземпляров PMT / (1 + i) мы можем сократить уравнение. Также с учетом аннуитета или обычного аннуитета, умножаем его на (1 + iT), и мы получаем
\ (PV = \ dfrac {PMTn} {(1 + i)} (1 + iT) \ tag {4} \)
Текущая стоимость бессрочного платежа (t → ∞ и n = mt → ∞)
Для вечности, вечной ренты, время и количество периодов стремятся к бесконечности, следовательно, n стремится к бесконечности.При увеличении n член 1 / (1 + i) n в формуле (2) переходит в 0, оставляя
\ (PV = \ dfrac {PMT} {i} (1 + iT) \ tag {5} \)
Текущая стоимость растущего бессрочного капитала (g
Аналогично для растущего бессрочного периода, где мы должны иметь g
\ (PV = \ dfrac {PMT} {(i-g)} (1 + iT) \ tag {6} \)
Текущая стоимость растущего бессрочного капитала (g = i) (t → ∞ и n = mt → ∞)
Поскольку n также стремится к бесконечности (n → ∞), когда t стремится к бесконечности (t → ∞), мы видим, что Текущая стоимость с растущей рентабельностью (g = i) также стремится к бесконечности
\ (PV = \ dfrac {PMTn} {(1 + i)} (1 + iT) \ rightarrow \ infty \ tag {7} \)
Формула приведенной стоимости для комбинированной суммы будущей стоимости и денежного потока (аннуитета):
Мы можем объединить уравнения (1) и (2), чтобы получить уравнение текущей стоимости, которое включает как единовременную выплату будущей стоимости, так и аннуитет. {mt}} \ right] (1 + (\ frac {r} {m}) T) \ tag {11} \)
{mt}} \ right] (1 + (\ frac {r} {m}) T) \ tag {11} \)
, где n = mt и \ (i = \ frac {r} {m} \). t — количество периодов, m — интервалы начисления процентов за период, а r — скорость за период t. (это легко понять, если использовать t в годах, r — номинальную ставку в год и m — интервалы начисления сложных процентов в год) Если записать в терминах i и n, i — это ставка за интервал начисления процентов, а n — общие интервалы начисления процентов, хотя это все еще может быть указано как «i — ставка за период, а n — количество периодов», где период = интервал начисления сложных процентов.«Период» может быть широким термином.
Относится к входам калькулятора, r = R / 100 и g = G / 100. Если начисление сложных процентов (m) и частота выплат (q) не совпадают в этих расчетах, r преобразуется в
эквивалентная ставка для совпадения с платежами, тогда n и i пересчитываются с точки зрения частоты платежей q. Первая часть уравнения — это
приведенная стоимость будущей суммы, а вторая часть — это
приведенная стоимость аннуитета.
Текущая стоимость бессрочного платежа (t → ∞ и n = mt → ∞)
Для бессрочного, бессрочного аннуитета количество периодов t стремится к бесконечности, следовательно, n стремится к бесконечности. В FV член в уравнении (11) переходит в 0, а 1 / (1 + i) n во втором члене также идет в 0, оставляя только формулу (5)
\ (PV = \ dfrac {PMT} {i} (1 + iT) \ tag {5} \)
Текущая стоимость растущего бессрочного капитала (g
Аналогично для растущего бессрочного периода, где мы должны иметь g
\ (PV = \ dfrac {PMT} {(i-g)} (1 + iT) \ tag {6} \)
Текущая стоимость растущего бессрочного капитала (g = i) (t → ∞ и n = mt → ∞)
Поскольку n также стремится к бесконечности (n → ∞), когда t стремится к бесконечности (t → ∞), мы видим, что Текущая стоимость с растущей рентабельностью (g = i) (10) стремится к бесконечности, и мы снова возвращаемся к уравнению (7)
\ (PV = \ dfrac {PMTn} {(1 + i)} (1 + iT) \ rightarrow \ infty \ tag {7} \)
Непрерывное смешивание (m → ∞)
Мы возвращаемся к формуле (11) для определения приведенной стоимости, где m — это сложное вознаграждение за период t, t — количество периодов, а r — сложная ставка с \ (i = \ frac {r} {m} \) и n. {rt}} \ справа] \ tag {12.г-1) Т) \ rightarrow \ infty \ tag {17} \)
{rt}} \ справа] \ tag {12.г-1) Т) \ rightarrow \ infty \ tag {17} \)
финансовых формул (с калькуляторами)
Люди из всех слоев общества, от студентов, биржевых маклеров и банкиров; риэлторам, домовладельцам и управляющим находят финансовые формулы невероятно полезными в повседневной жизни. Независимо от того, используете ли вы финансовые формулы для личных или по причинам образования, наличие доступа к правильным финансовым формулам может помочь улучшить вашу жизнь.
Независимо от того, в какой финансовой сфере вы работаете или изучаете, от корпоративных финансов до банковского дела, все они построены на тот же фундамент стандартных формул и уравнений. Хотя некоторые из этих сложных формул могут сбить с толку обычного человека, мы помочь, внося вам ясность.
Имеете ли вы дело со сложными процентами, аннуитетами, акциями или облигациями, инвесторы должны иметь возможность эффективно оценивать
уровень ценности или достоинства их финансовых показателей. Это делается путем оценки будущей прибыли и ее расчета относительно
текущая стоимость или эквивалентная норма прибыли.
Это делается путем оценки будущей прибыли и ее расчета относительно
текущая стоимость или эквивалентная норма прибыли.
FinanceFormulas.net может помочь.
Финансовая информация и калькуляторы на сайте FinanceFormulas.net предназначены не только для профессионалов, но и для всех, кто потребность в фундаментальных формулах, уравнениях и основных вычислениях, составляющих мир финансов. От студентов колледжа которые изучают финансы и бизнес, до профессионалов, занимающихся корпоративными финансами, FinanceFormulas.сеть поможет вам найти финансовые формулы, уравнения и калькуляторы, необходимые для достижения успеха.
Кто может получить больше всего от FinanceFormulas.net?
Студенты, изучающие финансы и бизнес, могут использовать формулы и
калькуляторы, бесплатно предоставляемые FinanceFormulas.net в качестве постоянного справочника, во время учебы в школе, затем во время работы в
мир финансов.
Люди, уже работающие в сфере бизнеса , которые могут иметь Если вы забыли, как использовать определенную формулу или набор уравнений, наши инструменты станут бесценным ресурсом.FinanceFormulas.net не только упрощает поиск формулы, уравнения или калькулятора, которые вы ищете, мы упрощаем добавление формулы в закладки, чтобы вы больше никогда не придется тратить время на поиск нужного инструмента.
Любой . Люди любого возраста могут пользоваться калькуляторами в FinanceFormulas.net, чтобы помочь им справляться с финансовыми трудностями повседневной жизни. Ипотека, задолженность по кредитной карте или понимание академической оценки вашего инвестиции, такие как акции и облигации, он имеет доступ к правильным формулам, уравнениям и калькуляторам, которые могут помочь вам проложите свой путь к финансово благополучной жизни.
Планируете ли вы использовать бесплатные формулы, предоставляемые FinanceFormulas. net, для личного или академического использования,
FinanceFormulas.net здесь, чтобы помочь вам найти банковские формулы, формулы акций и облигаций, корпоративные и прочие.
формулы, которые вам нужны.
net, для личного или академического использования,
FinanceFormulas.net здесь, чтобы помочь вам найти банковские формулы, формулы акций и облигаций, корпоративные и прочие.
формулы, которые вам нужны.
Вернуться к началу
Временная стоимость денег — Как рассчитать PV и FV денег
Какова временная стоимость денег?
Временная стоимость денег — это базовая финансовая концепция, согласно которой деньги в настоящем стоят больше, чем та же сумма денег, которая будет получена в будущем.Это верно, потому что деньги, которые у вас есть прямо сейчас, можно инвестировать и получить прибыль, таким образом создавая большую сумму денег в будущем. (Кроме того, с будущими деньгами существует дополнительный риск того, что деньги могут никогда не быть получены по той или иной причине.) Временная стоимость денег иногда называется чистой приведенной стоимостью. Чистая приведенная стоимость (NPV). Чистая приведенная стоимость. (NPV) — это стоимость всех будущих денежных потоков (положительных и отрицательных) в течение всего срока действия инвестиции, дисконтированная до настоящего времени.(NPV) денег.
(NPV) — это стоимость всех будущих денежных потоков (положительных и отрицательных) в течение всего срока действия инвестиции, дисконтированная до настоящего времени.(NPV) денег.
Как работает временная стоимость денег
Можно использовать простой пример, чтобы показать временную стоимость денег. Предположим, что кто-то предлагает заплатить вам одним из двух способов за некоторую работу, которую вы выполняете для них: они либо заплатят вам 1000 долларов сейчас, либо 1100 долларов через год.
Какой вариант оплаты выбрать? Это зависит от того, какой вид возврата инвестиций. Норма возврата. Норма прибыли (ROR) — это прибыль или убыток от инвестиции за период времени, сопоставленная с первоначальной стоимостью инвестиций, выраженной в процентах.В этом руководстве представлены наиболее распространенные формулы, которые вы можете заработать на деньги в настоящее время. Поскольку 1100 долларов составляют 110% от 1000 долларов, то, если вы считаете, что можете получить более 10% прибыли на деньги, вложив их в течение следующего года, вам следует выбрать 1000 долларов сейчас.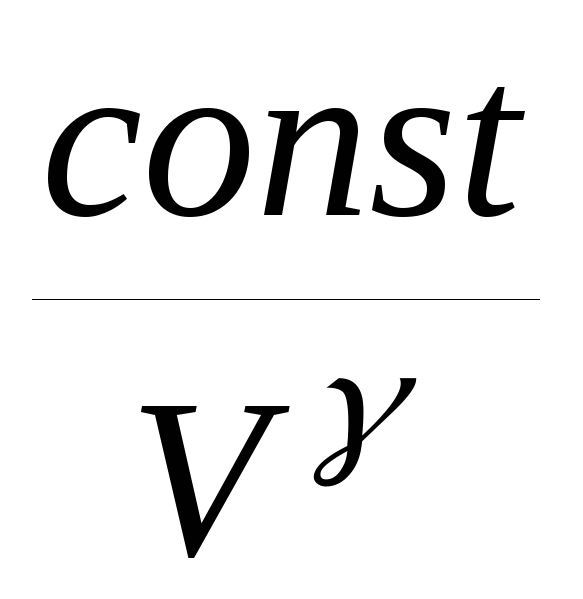 С другой стороны, если вы не думаете, что сможете заработать более 9% в следующем году, вложив деньги, вам следует взять будущий платеж в размере 1100 долларов — при условии, что вы доверяете тому, кто заплатит вам тогда.
С другой стороны, если вы не думаете, что сможете заработать более 9% в следующем году, вложив деньги, вам следует взять будущий платеж в размере 1100 долларов — при условии, что вы доверяете тому, кто заплатит вам тогда.
Временная стоимость и покупательная способность
Временная стоимость денег также связана с концепциями инфляции и покупательной способности.Необходимо принять во внимание оба фактора, а также любую норму прибыли, которую можно получить при вложении денег.
Почему это важно? Потому что инфляция постоянно подрывает стоимость, а следовательно, и покупательную способность денег. Лучшим примером этого являются цены на такие товары, как газ или продукты питания. Если, например, вам выдали сертификат на 100 долларов бесплатного бензина в 1990 году, вы могли бы купить намного больше галлонов бензина, чем вы могли бы получить, если бы вам дали 100 долларов бесплатного бензина десять лет спустя.
При инвестировании денег необходимо учитывать инфляцию и покупательную способность, потому что для расчета реальной доходности инвестиций вы должны вычесть уровень инфляции из любого процентного дохода, который вы зарабатываете на свои деньги. Если уровень инфляции на самом деле выше, чем доходность ваших инвестиций, то, даже если ваши инвестиции показывают номинальную положительную доходность, вы фактически теряете деньги с точки зрения покупательной способности. Например, если вы зарабатываете 10% на инвестициях, но уровень инфляции составляет 15%, вы фактически теряете 5% покупательной способности каждый год (10% — 15% = -5%).
Если уровень инфляции на самом деле выше, чем доходность ваших инвестиций, то, даже если ваши инвестиции показывают номинальную положительную доходность, вы фактически теряете деньги с точки зрения покупательной способности. Например, если вы зарабатываете 10% на инвестициях, но уровень инфляции составляет 15%, вы фактически теряете 5% покупательной способности каждый год (10% — 15% = -5%).
Формула временной стоимости денег
Временная стоимость денег является важным понятием не только для людей, но и для принятия деловых решений. Компании учитывают временную стоимость денег при принятии решений об инвестировании в разработку новых продуктов, приобретении нового бизнес-оборудования или производственных мощностей, а также при установлении условий кредитования Соглашение о купле-продажеСоглашение о купле-продаже (SPA) представляет собой результат ключевых коммерческих и ценовых переговоров. По сути, он устанавливает согласованные элементы сделки, включает ряд важных мер защиты для всех вовлеченных сторон и обеспечивает правовую основу для завершения продажи собственности. для продажи своих товаров или услуг.
для продажи своих товаров или услуг.
Для расчета будущей стоимости денег можно использовать специальную формулу, чтобы ее можно было сравнить с приведенной стоимостью:
Где:
FV = будущая стоимость денег
PV = приведенная стоимость
i = процентная ставка или другой доход, который можно заработать на деньги
t = количество лет, которые необходимо учитывать
n = количество периодов начисления сложных процентов в год
Используя приведенную выше формулу, давайте рассмотрим пример, в котором у вас есть 5000 долларов и вы можете рассчитывать на получение 5% годовых с этой суммы каждый год в течение следующих двух лет.(1 x 2) = 5 512,50 долларов США
Формула приведенной стоимости будущих денег
Формула также может использоваться для расчета приведенной стоимости денег, которые будут получены в будущем. (1 x 1) = 1047 долларов США
(1 x 1) = 1047 долларов США
Расчет выше показывает, что при доступной доходности 5% годовых вы необходимо будет получить 1047 долларов в настоящем, чтобы равняться будущей стоимости в 1100 долларов, которые будут получены через год.
Чтобы упростить вам задачу, существует ряд онлайн-калькуляторов для расчета будущей или текущей стоимости денег.
Пример чистой приведенной стоимости
Ниже показано, как выглядит чистая приведенная стоимость ряда денежных потоков. Как видите, будущая стоимость денежных потоков указана в верхней части диаграммы, а текущая стоимость денежных потоков показана синими полосами в нижней части диаграммы.
Этот пример взят из бесплатного курса CFI «Введение в корпоративные финансы», в котором эта тема рассматривается более подробно.
Дополнительные ресурсы
Мы надеемся, что вам понравилось объяснение CFI о временной стоимости денег. Чтобы узнать больше о деньгах и инвестировании, ознакомьтесь со следующими ресурсами:
- Скорректированная приведенная стоимость Скорректированная приведенная стоимость (APV) Скорректированная приведенная стоимость (APV) проекта рассчитывается как его чистая приведенная стоимость плюс приведенная стоимость побочных эффектов заемного финансирования.
 .
. - Методы прогнозированияМетоды прогнозированияЛучшие методы прогнозирования. В этой статье мы объясним четыре типа методов прогнозирования доходов, которые финансовые аналитики используют для прогнозирования будущих доходов.n], где PV = текущая стоимость, F = будущий платеж (денежный поток), r = ставка дисконтирования, n = количество периодов в будущем
- Методы оценки Методы оценки При оценке компании как непрерывно действующей существуют три основных метода оценки. использовано: DCF-анализ, сопоставимые компании и прецедентные сделки
Текущая стоимость (PV)
Деньги сейчас дороже денег позже .
Почему? Потому что вы можете использовать деньги, чтобы заработать больше денег!
Вы можете вести бизнес, или купить что-то сейчас, а потом продать дороже, или просто положить деньги в банк, чтобы заработать проценты.
Пример: Вы можете получить 10% годовых на свои деньги.
Итак, 1000 долларов сейчас может заработать 1000 долларов x 10% = 100 долларов в год.
Ваши 1000 долларов сейчас могут превратиться в 1100 долларов через год .
Текущая стоимость
Итак, 1000 долларов сейчас — это , те же , что и 1100 долларов в следующем году (под 10% годовых).
Мы говорим, что приведенная стоимость из 1100 долларов в следующем году составит 1000 долларов
Потому что мы могли бы превратить 1000 долларов в 1100 долларов (если бы мы могли заработать 10%).
Теперь давайте расширим эту идею на будущее …
Как рассчитать будущие платежи
Давайте останемся с 10% годовых. Это означает, что деньги растут на 10% каждый год, например:
Итак:
- 1100 долларов в следующем году то же самое, что и 1000 долларов сейчас .
- И 1210 долларов через 2 года это то же самое, что 1000 долларов сейчас .
- и т. Д.
На самом деле все эти суммы равны (учитывая , когда они возникают, и 10% -ный процент).
Более простой расчет
Но вместо «прибавления 10% к каждому году» проще умножить на 1,10 (объяснено в разделе «Сложный процент»):
Итак, мы получаем это (тот же результат, что и выше):
Назад в будущее
И чтобы увидеть, сколько денег в будущем стоит сейчас , вернемся назад (деление на 1,10 каждый год вместо умножения):
Пример: Сэм обещает вам
500 долларов в следующем году , какова текущая стоимость?Чтобы вернуть будущий платеж на один год разделите на 1.10
Итак, 500 долларов в следующем году это 500 долларов ÷ 1,10 = 454,55 долларов сейчас (с точностью до цента).
Текущая стоимость $ 454,55
Пример: Алекс обещает вам
900 долларов через 3 года , какова текущая стоимость?Чтобы отсчитать будущий платеж назад на три года разделите на 1,10 трижды
Итак 900 долларов за 3 года это:
$ 900 ÷ 1. 10 ÷ 1,10 ÷ 1,10
10 ÷ 1,10 ÷ 1,10
$ 900 ÷ (1,10 × 1,10 × 1,10)
$ 900 ÷ 1,331
676,18 $ сейчас (с точностью до цента).
Лучше с экспонентами
Но вместо $ 900 ÷ (1,10 × 1,10 × 1,10) лучше использовать экспоненты (показатель степени говорит , сколько раз использовать при умножении).
Пример: (продолжение)
Текущая стоимость 900 долларов за 3 года (за один раз):
$ 900 ÷ 1.10 3 = 676,18 $ сейчас (с точностью до цента).
Как формула это:
PV = FV / (1 + r) n
- PV — текущая стоимость
- FV — будущая стоимость
- r — процентная ставка (в десятичном формате, то есть 0,10, а не 10%)
- n — количество лет
Пример: (продолжение)
Используйте формулу для расчета приведенной стоимости 900 долларов за 3 года :
PV = FV / (1 + r) n
ЛС = 900 $ / (1 + 0. 10) 3 = 900 $ / 1,10 3 = 676,18 $ (с точностью до цента).
10) 3 = 900 $ / 1,10 3 = 676,18 $ (с точностью до цента).
Показатели проще использовать, особенно с калькулятором. Например, 1,10 6 быстрее, чем 1,10 × 1,10 × 1,10 × 1,10 × 1,10 × 1,10 |
Давайте еще немного воспользуемся формулой:
Пример: Сколько сейчас стоит 570 долларов в следующем году при процентной ставке 10%?
PV = 570 $ / (1 + 0.10) 1 = 570 долларов / 1,10 = 518,18 долларов (с точностью до цента)
Но ваш выбор процентной ставки может все изменить!
Пример: Сколько сейчас стоит 570 долларов в следующем году при процентной ставке 15%?
PV = 570 долларов США / (1 + 0,15) 1 = 570 долларов США / 1,15 = долларов США 495,65 долларов США (с точностью до цента)
Или что делать, если не получишь деньги 3 года
Пример: Сколько сейчас стоит 570 долларов через 3 года при процентной ставке 10%?
PV = 570 $ / (1 + 0.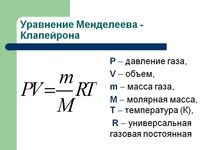 10) 3 = 570 долларов / 1,331 = 428,25 долларов (с точностью до цента)
10) 3 = 570 долларов / 1,331 = 428,25 долларов (с точностью до цента)
Последний пример:
Пример: Вам обещают 800 долларов через 10 лет. Какова его текущая стоимость при процентной ставке 6%?
PV = 800 долл. США / (1 + 0,06) 10 = 800 долл. США / 1,7908 долл. США … = долл. США 446,72 долл. США (с точностью до цента)
Общие сведения о формулах приведенной стоимости — PropertyMetrics
Важно понимать математику, лежащую в основе расчетов приведенной стоимости, потому что это поможет вам увидеть, что на самом деле происходит в калькуляторе или электронной таблице.А как только вы разберетесь с математикой, расчеты станут намного более интуитивно понятными. Тем не менее, многим людям сложно понять формулы и расчеты приведенной стоимости. В этом посте мы подробно рассмотрим формулу текущей стоимости паушальной суммы, формулу текущей стоимости аннуитета и, наконец, формулу чистой приведенной стоимости для нерегулярного потока денежных средств.
Интуиция за настоящей стоимостью
Во-первых, прежде чем приступить к математике, лежащей в основе расчета приведенной стоимости, давайте на минутку концептуально поразмыслим над идеей временной стоимости денег.
Если я предлагаю вам иметь 1000 долларов сегодня или 1000 долларов через год, что бы вы выбрали? Если вы разумное существо, вы выберете 1000 долларов сегодня. Почему? Потому что есть риск, связанный с ожиданием получения денег через год. Я могу потерять все свои деньги, уехать туда, где вы меня не найдете, или умереть в течение следующего года. Другими словами, есть риск, что вы действительно не получите 1000 долларов в год.
Экономический термин для этой концепции — «неприятие риска», что означает, что при прочих равных, рациональные инвесторы предпочитают меньший риск.Вдобавок, если я дам вам 1000 долларов сегодня, вы также можете инвестировать их на один год и получить более 1000 долларов в конце года. По этим причинам деньги имеют «временную стоимость», которая создает математическую связь между текущей стоимостью в долларах и будущей стоимостью в долларах. Давайте подробнее рассмотрим эту взаимосвязь, чтобы вывести формулу приведенной стоимости единовременной выплаты.
Давайте подробнее рассмотрим эту взаимосвязь, чтобы вывести формулу приведенной стоимости единовременной выплаты.
Это подводит нас к теме процентов и процентных ставок.Как рациональный инвестор, не склонный к риску, вам требуется дополнительная компенсация, чтобы подождать год до получения денег. Количество дополнительных денег, которые вам нужно подождать, является косвенным показателем вашей личной процентной ставки. Эта процентная ставка представляет собой меру упущенной альтернативной стоимости инвестиций, рыночного риска и инвестиционного риска. Предположим, вы соглашаетесь подождать один год до получения денег, если вам обещают 1100 долларов или 10% процентную ставку. Математически этот расчет показывает, что будущая стоимость (FV) равна текущей стоимости (PV) плюс дополнительные проценты, которые вам требуются в качестве компенсации за время и риск (PV * R).
1100 долларов = 1000 долларов + (1000 долларов * 0,10)
FV = PV + (PV * R) = PV (1 + R)
Эта концепция временной стоимости денег и математическая взаимосвязь являются ключевыми для понимания расчета приведенной стоимости. Это также позволяет нам рассмотреть противоположные отношения или то, как текущая стоимость соотносится с будущей стоимостью. Например, сколько вы готовы заплатить сегодня за обещание 1100 долларов в год? Используя ту же требуемую норму прибыли, 10%, мы можем подсчитать, что стоимость этих инвестиций сегодня составляет 1000 долларов.
PV = FV / (1 + R)
1000 долларов = 1100 долларов / 1,10
Формула текущей стоимости единовременной выплаты с несколькими периодами начисления процентов
В предыдущем примере процентная ставка имела только один период начисления сложных процентов. Однако по большинству инвестиций начисляются сложные проценты чаще, чем один раз в год. Ежемесячное или ежедневное начисление сложных процентов гораздо более распространено, чем годовое начисление процентов. Инвесторы также выигрывают от увеличения частоты сложных процентов.
Ежемесячное или ежедневное начисление сложных процентов гораздо более распространено, чем годовое начисление процентов. Инвесторы также выигрывают от увеличения частоты сложных процентов.
Подумайте, как расчет будущей стоимости в нашем примере выше изменится с полугодовым начислением сложных процентов. Вместо одного периода начисления сложных процентов теперь 2 в год. Таким образом, указанная процентная ставка 10% делится на количество периодов начисления сложных процентов, и количество периодов начисления сложных процентов также увеличивается. Это означает, что теперь мы зарабатываем 5% за период, всего 2 периода.
В первом периоде 1000 долларов увеличиваются на 5% до 1050 долларов, а во втором периоде 1050 долларов приносят еще 5% процентов на общую сумму 1102 доллара.50.
Период 1:
1000 $ (1.05) = 1050 $
Период 2:
1050 долл. США (1,05) = 1 102,50 долл. США
Другими словами, формула добавляет еще один компонент (N) для представления количества периодов начисления сложных процентов.
1 102,50 = 1 000 долларов США (1 + 10/2) 2
FV = PV (1 + R / N) N
PV = FV / (1 + R / N) N
Кроме того, обратите внимание, как увеличение частоты начисления сложных процентов также увеличивает фактическую реализованную норму прибыли.В этом примере заявленная процентная ставка составляла 10%, но реализованная годовая норма доходности составила 102,50 долл. США / 1000 долл. США, или 10,25%. Эта фактическая реализованная норма прибыли известна как эффективная годовая ставка (EAR).
Формула приведенной стоимости аннуитета Затем вы можете расширить эту базовую математическую основу для расчета приведенной стоимости более чем одного денежного потока. Рассмотрим базовую модель, в которой проценты начисляются ежегодно, и вы получите выплату в размере 1100 долларов в течение одного года.Теперь вы также получите выплату в размере 1100 долларов в конце второго года. Приведенная стоимость теперь представляет собой сумму дисконтирования одного платежа в размере 1100 долларов за один год до настоящего времени, а также одного платежа в размере 1100 долларов за два года до настоящего времени.
PV = 1,100 / (1,10) 1 + 1,100 / (1,10) 2 = 1909,09 долл. США
Если все платежи остаются неизменными, то есть здесь вы получаете одни и те же 1100 долларов каждый период, есть особый способ объединить все эти условия в формулу, известную как приведенная стоимость аннуитета.Числитель дроби (1100 долларов) не меняется, и единственная часть формулы, которая действительно изменяется, — это количество периодов, в течение которых конкретный денежный поток дисконтируется (показатель степени 1,10 в знаменателе). Обобщенная формула для приведенной стоимости потока денежных средств представлена в следующем уравнении, где P — платеж или денежный поток, полученный в течение периода, R — периодическая норма прибыли, а N — количество периодов.
Математически это также известно как геометрический ряд.Когда все денежные потоки одинаковы (P), коэффициенты дисконтирования можно упростить особым образом. В этом случае уравнение приведенной стоимости можно упростить следующим образом:
Формула чистой приведенной стоимости для неравномерного потока денежных средств В то время как приведенная выше формула аннуитета полезна для оценки аннуитета или ипотечной ссуды, в которой платеж не изменяется, эта формула не особенно полезна при вычислении стоимости инвестиции с различными денежными потоками. Математическая концепция дисконтирования будущих денежных потоков до настоящего времени не меняется, но мы даем формуле другое название. Формула для чистой приведенной стоимости просто суммирует будущие денежные потоки (C) после их дисконтирования до настоящего времени.
Математическая концепция дисконтирования будущих денежных потоков до настоящего времени не меняется, но мы даем формуле другое название. Формула для чистой приведенной стоимости просто суммирует будущие денежные потоки (C) после их дисконтирования до настоящего времени.
Формула чистой приведенной стоимости также отдельно учитывает любые первоначальные затраты, понесенные в начале инвестиции (C 0 ). Поскольку размер денежных потоков меняется, эту формулу нельзя свести к простому геометрическому ряду.Итак, формулу чистой приведенной стоимости можно упростить следующим образом:
Пример
Расчет чистой приведенной стоимости — важный инструмент при расчете стоимости коммерческой недвижимости. Например, предположим, что у вас есть проформа отчетов о движении денежных средств по собственности и вы хотите оценить разумную цену покупки сегодня. Чистая операционная прибыль оценивается в 35 000 долларов в год 1, 37 000 долларов в год 2, 38 000 долларов в год 3, 40 000 долларов в год 4 и 41 000 долларов в год 5. После пяти лет владения недвижимостью вы ожидаете, что продажная цена составит 450 000 долларов. У вас есть необходимая норма доходности, равная 8%. Итак, вы используете следующее уравнение:
После пяти лет владения недвижимостью вы ожидаете, что продажная цена составит 450 000 долларов. У вас есть необходимая норма доходности, равная 8%. Итак, вы используете следующее уравнение:
NPV = 35,000 / (1,08) 1 + 37,000 / (1,08) 2 + 38,000 / (1,08) 3 + 40,000 / (1,08) 4 + 491,000 / (1,08) 5
NPV = 457 862 долл. США
Другими словами, ваша оценочная стоимость этой собственности составляет 457 862 доллара. Сегодняшняя стоимость определяется предполагаемыми денежными потоками, которые вы ожидаете получить в будущем после дисконтирования до настоящего времени с использованием процентной ставки, которая отражает вашу неуверенность (неприятие риска) в отношении суммы и сроков этих денежных потоков.
Расчет приведенной стоимости | AccountingCoach
Самый простой и точный способ рассчитать текущую стоимость любых будущих сумм (единичная сумма, различные суммы, аннуитеты) — использовать электронный финансовый калькулятор или компьютерное программное обеспечение. Некоторые электронные финансовые калькуляторы теперь доступны менее чем за 35 долларов.
Некоторые электронные финансовые калькуляторы теперь доступны менее чем за 35 долларов.
ВАЖНО! Поймите, что каждый финансовый калькулятор работает по-своему и может работать не так, как в нашем Разъяснении.Обязательно прочтите и полностью усвойте инструкции перед использованием любого калькулятора или компьютерного программного обеспечения. Одно неверное предположение, один неверный ввод или использование кнопки, которая работает не так, как вы предполагали, будет означать неправильный ответ — а это может иметь значительные финансовые последствия!
Если у вас нет доступа к электронному финансовому калькулятору или программному обеспечению, простой способ рассчитать суммы приведенной стоимости — использовать таблицы приведенной стоимости (таблицы PV).Таблицы PV не могут обеспечить такой же уровень точности, как финансовые калькуляторы или компьютерное программное обеспечение, потому что коэффициенты, используемые в таблицах, округлены до меньшего числа десятичных знаков.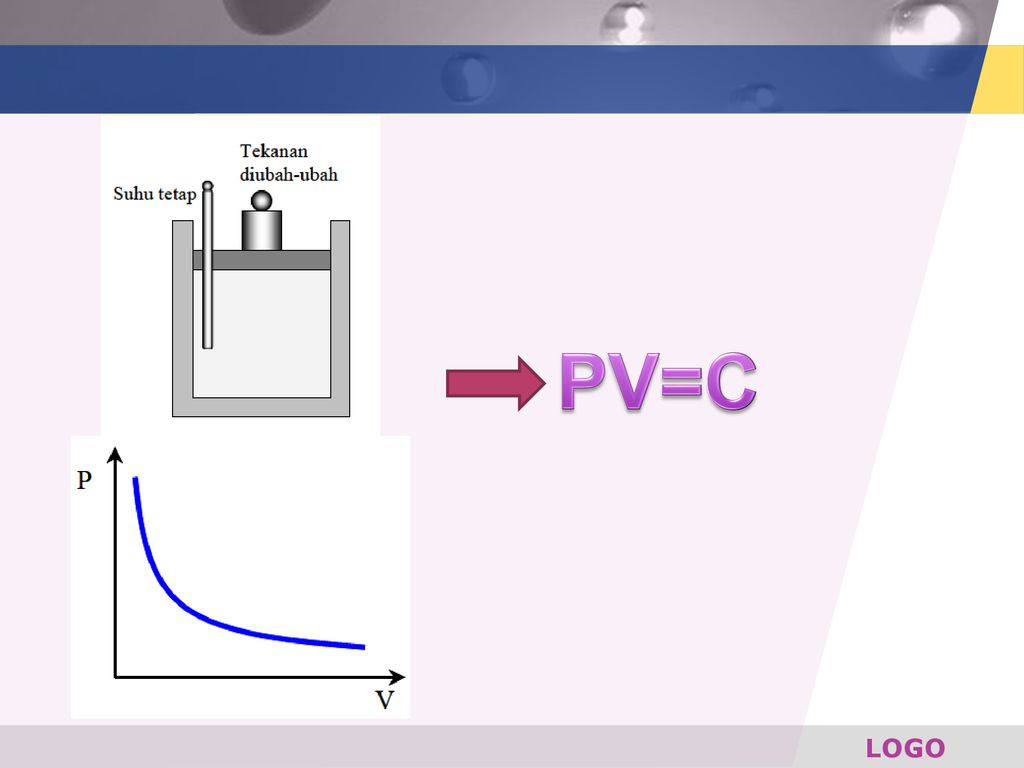 Кроме того, они обычно содержат ограниченное количество вариантов процентных ставок и периодов времени. Несмотря на это, таблицы приведенной стоимости остаются популярными в академической среде, поскольку их легко включить в учебник. Поскольку они широко используются, мы будем использовать таблицы приведенной стоимости для решения наших примеров.
Кроме того, они обычно содержат ограниченное количество вариантов процентных ставок и периодов времени. Несмотря на это, таблицы приведенной стоимости остаются популярными в академической среде, поскольку их легко включить в учебник. Поскольку они широко используются, мы будем использовать таблицы приведенной стоимости для решения наших примеров.
За каждой таблицей, калькулятором и программным обеспечением стоят математические формулы , необходимые для вычисления сумм приведенной стоимости, процентных ставок, количества периодов и сумм будущей стоимости.Вначале мы покажем вам несколько примеров того, как использовать формулу приведенной стоимости в дополнение к таблицам PV.
За исключением незначительных различий из-за округления, ответы на приведенные ниже уравнения будут одинаковыми, независимо от того, вычисляются ли они с помощью финансового калькулятора, компьютерного программного обеспечения, таблиц PV или формул.
Расчет текущей стоимости единой суммы (PV)
В этом разделе мы продемонстрируем, как найти текущую стоимость отдельной будущей денежной суммы, такой как квитанция или платеж. Мы будем называть приведенную стоимость отдельной суммы PV .
Мы будем называть приведенную стоимость отдельной суммы PV .
Упражнение № 1
Предположим, мы должны получить 100 долларов в конце двух лет. Как рассчитать приведенную стоимость суммы, предполагая, что процентная ставка составляет 8% годовых, начисленных ежегодно?
На следующей временной шкале изображена известная нам информация вместе с неизвестным компонентом (PV):
Расчет по формуле PV
Формула приведенной стоимости для отдельной суммы:
Используя вторую версию формулы, решение:
Ответ, 85 $.73 , говорит нам, что получить 100 долларов через два года — это то же самое, что получить 85,73 доллара сегодня, если временная стоимость денег составляет 8% годовых, начисленных ежегодно. («Сегодня» — это то же понятие, что и «период времени 0»)
Расчет с использованием PV 1 Таблица
Обычно в учебниках по бухгалтерскому учету и финансам есть таблицы приведенной стоимости для использования при расчете сумм приведенной стоимости. В таблице PV, равной 1, каждый заголовок столбца отображает процентную ставку (i), а строка указывает количество периодов в будущем, прежде чем возникнет сумма (n).На пересечении каждого столбца и строки находится коррелирующее приведенное значение коэффициента 1 (PV = 1). Фактор PV 1 говорит нам, какой будет приведенная стоимость в период времени 0 для отдельной суммы в 1 доллар в конце периода времени (n). Щелкните следующее, чтобы увидеть приведенную стоимость 1 таблицы: PV из 1 таблицы .
В таблице PV, равной 1, каждый заголовок столбца отображает процентную ставку (i), а строка указывает количество периодов в будущем, прежде чем возникнет сумма (n).На пересечении каждого столбца и строки находится коррелирующее приведенное значение коэффициента 1 (PV = 1). Фактор PV 1 говорит нам, какой будет приведенная стоимость в период времени 0 для отдельной суммы в 1 доллар в конце периода времени (n). Щелкните следующее, чтобы увидеть приведенную стоимость 1 таблицы: PV из 1 таблицы .
Таблица PV 1 имеет два ограничения: (1) значения округляются (в нашей таблице округлено до трех знаков после запятой для простоты использования), и, таким образом, таблица жертвует точностью, и (2) таблица отображает только ограниченное количество знаков после запятой. количество вариантов ставок и лет.
После определения PV 1 фактора из таблицы просто используйте его для замены следующего члена в формуле PV: [1 ÷ (1 + i) n ]
Используя данные, представленные в Упражнении № 1, мы можем определить приведенную стоимость получения 100 долларов в конце двух лет с дисконтированием по процентной ставке 8% годовых:
Поскольку для PV 1 таблицы были округлены коэффициенты до трех десятичных знаков, ответ (85,70 долларов США) немного отличается от суммы, рассчитанной по формуле PV (85 долларов США. 73). В любом случае ответ говорит нам, что 100 долларов в конце двух лет эквивалентны получению примерно 85,70 доллара сегодня (в период времени 0), если временная стоимость денег составляет 8% годовых, начисленных ежегодно.
73). В любом случае ответ говорит нам, что 100 долларов в конце двух лет эквивалентны получению примерно 85,70 доллара сегодня (в период времени 0), если временная стоимость денег составляет 8% годовых, начисленных ежегодно.
Упражнение № 2
Нам нужно рассчитать приведенную стоимость (стоимость в период времени 0) получения единовременной суммы в 1000 долларов за 20 лет. Процентная ставка дисконтирования будущей суммы оценивается в 10% годовых, начисленных ежегодно.
На следующей временной шкале изображена известная нам информация вместе с неизвестным компонентом (PV):
Расчет с использованием формулы PV 1
Используя формулу для определения приведенной стоимости, мы имеем:
Ответ говорит нам, что получение 1000 долларов через 20 лет эквивалентно получению 148 долларов.64 сегодня, если временная стоимость денег составляет 10% годовых, начисленных ежегодно.
Расчет с использованием PV 1 Таблица
Используйте таблицу PV 1, чтобы найти (округленный) коэффициент приведенной стоимости на пересечении n = 20 и i = 10%.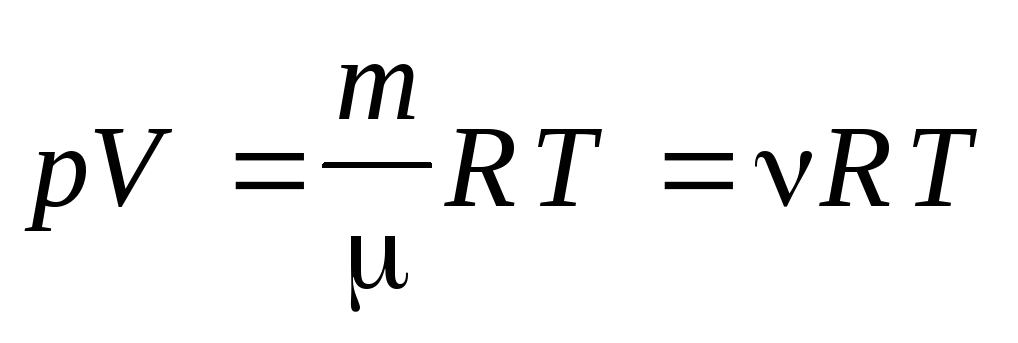 Чтобы рассчитать приведенную стоимость получения 1000 долларов США по истечении 20 лет с процентной ставкой 10%, введите коэффициент в формулу:
Чтобы рассчитать приведенную стоимость получения 1000 долларов США по истечении 20 лет с процентной ставкой 10%, введите коэффициент в формулу:
Мы видим, что приведенная стоимость получения 1000 долларов через 20 лет эквивалентна получению примерно 149 долларов.00 сегодня, если временная стоимость денег составляет 10% годовых, начисленных ежегодно.
Упражнение № 3
Какова приведенная стоимость получения единой суммы в 5000 долларов по истечении трех лет, если временная стоимость денег составляет 8% в год, составляющих ежеквартально ?
На следующей временной шкале изображена известная нам информация вместе с неизвестным компонентом (PV):
Обратите внимание, что на временной шкале показано n = 12, потому что в трехлетнем периоде 12 кварталов.Поскольку периоды времени составляют три месяца, ставка дисконтирования равна i = 2% (квартальная ставка , которая получается из годовой ставки 8%, деленной на четыре квартала каждого года).
Расчет с использованием формулы PV
Используя формулу для определения приведенной стоимости, мы имеем:
Ответ говорит нам, что получение 5000 долларов через три года после сегодняшнего дня эквивалентно получению 3942,45 доллара сегодня, если временная стоимость денег составляет 8% годовых, что составляет ежеквартально .
Расчет с использованием PV 1 Таблица
Приведенная стоимость получения 5000 долларов в конце трех лет, когда процентная ставка начисляется ежеквартально , требует, чтобы (n) и (i) были указаны в кварталах. Используйте PV из 1 таблицы , чтобы найти (округленную) приведенную стоимость на пересечении n = 12 (3 года x 4 квартала) и i = 2% (8% в год ÷ 4 квартала). Подставьте множитель в формулу:
Мы видим, что приведенная стоимость получения 5000 долларов через три года после сегодняшнего дня составляет примерно 3940 долларов.00, если временная стоимость денег составляет 8% в год, начисляется ежеквартально.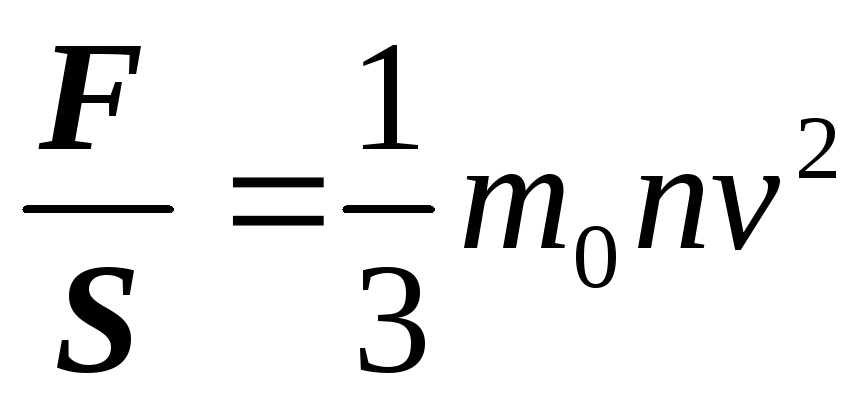
Упражнение № 4
Какова приведенная стоимость получения единовременной суммы в размере 10 000 долларов в конце пяти лет, если временная стоимость денег составляет 6% в год, составляющих за полгода ?
На следующей временной шкале изображена известная нам информация вместе с неизвестным компонентом (PV):
Обратите внимание, что на временной шкале показано n = 10, потому что в пятилетнем периоде 10 шестимесячных (или полугодовых) периодов.Поскольку начисление сложных процентов происходит раз в полгода, ставка дисконтирования составляет i = 3% за шестимесячный период (годовая ставка 6%, деленная на два полугодовых периода в каждом году).
Расчет с использованием формулы PV
Используя формулу для определения приведенной стоимости, мы имеем:
Ответ говорит нам, что получение 10 000 долларов через пять лет после сегодняшнего дня эквивалентно получению 7 440,90 долларов сегодня, если временная стоимость денег имеет годовую норму 6%, составляющую за полугодие .
Расчет с использованием PV 1 Таблица
Для приведенной стоимости получения 10000 долларов в конце пяти лет, когда начисление сложных процентов является полугодовым, необходимо, чтобы n = 10 (5 лет X 2 полугодовых периода в год) и i = 3% (6% в год ÷ два полугодовых периода в каждом году). Используйте PV из 1 таблицы , чтобы найти (округленный) коэффициент приведенной стоимости на пересечении n = 10 и i = 3%. Подставьте множитель в формулу:
Мы видим, что приведенная стоимость получения 10 000 долларов через пять лет эквивалентна получению примерно 7 440 долларов.00:00 сегодня, если временная стоимость денег составляет 6% в год, составляет за полугодие .
Текущая стоимость | Формула и определение
Что такое приведенная стоимость?
Приведенная стоимость (PV) измеряет текущую стоимость денежной суммы или потока денежных средств, ожидаемых в будущем. Эта стоимость будет отличаться от номинальной стоимости денежных потоков, поскольку само время влияет на стоимость. Время представляет собой расстояние от денег, а расстояние создает риск, который компенсирует стоимость.При инвестировании риск компенсируется процентами или доходами для инвесторов.
Время представляет собой расстояние от денег, а расстояние создает риск, который компенсирует стоимость.При инвестировании риск компенсируется процентами или доходами для инвесторов.
Приведенная стоимость — это сопоставимая стоимость наличных денег в будущем.
Почему важна приведенная стоимость
Текущая стоимость важна, потому что она позволяет инвесторам сравнивать значения в динамике. PV может помочь инвесторам оценить будущие финансовые выгоды от текущих активов или обязательств. При использовании в таких областях, как финансовое моделирование, оценка акций и ценообразование облигаций, инвесторы могут рассчитать текущую стоимость на основе их будущей доходности.
Например, если инвестору нужно сравнить два типа инвестиций, он может оценить, какой из них предлагает лучшую доходность, сравнив их текущую стоимость.
Как рассчитать приведенную стоимость
Формула PV снижает будущую стоимость актива до его сегодняшней стоимости. Расчет приведенной стоимости включает рассмотрение предполагаемой годовой нормы прибыли (будь то инфляция или ожидаемые проценты от инвестиций). Эта часть формулы также называется «ставкой дисконтирования» или ставкой, при которой время влияет на стоимость, где приведенная стоимость с формулой ставки дисконтирования даст упущенную норму прибыли, если вы примете денежную сумму в будущем. по сравнению с сегодняшним днем.
Эта часть формулы также называется «ставкой дисконтирования» или ставкой, при которой время влияет на стоимость, где приведенная стоимость с формулой ставки дисконтирования даст упущенную норму прибыли, если вы примете денежную сумму в будущем. по сравнению с сегодняшним днем.
Другие элементы формулы приведенной стоимости включают рассмотрение количества периодов выплат и будущей стоимости (также известной как прогнозируемая сумма денег в будущем).
Формула приведенной стоимости
Формула приведенной стоимости выглядит следующим образом:
Пример формулы текущей стоимости
Вы ожидаете получить 50 000 долларов через десять лет, предполагая годовую ставку 5%, вы можете найти значение этой суммы сегодня .
Используйте следующую формулу:
PV = 50 000 долл. США / (1 + 0.05) 10
= 30 695,66 долларов США
Это означает, что приведенная стоимость ваших инвестиций составляет 30 695,66 долларов США.
Как рассчитать PV в Excel
Самый точный (и самый простой) метод расчета приведенной стоимости — использовать финансовый калькулятор или Microsoft Excel. Фактически, в Excel есть встроенная функция, которая поможет вам рассчитать PV.
Фактически, в Excel есть встроенная функция, которая поможет вам рассчитать PV.
Давайте воспользуемся приведенным выше примером, чтобы узнать, как рассчитать PV в Excel. Вот что вы делаете:
Напишите слово «Год» в первой ячейке (A1), затем запишите годы с 0 по 10 в ячейки с B1 по K1.
Напишите слово «Процентная ставка» в ячейке A2, затем введите 5% для ячеек с C2 по L2
Напишите слово «Будущая стоимость» в ячейке A3 и запишите 50 000 долларов в ячейку L3
Напишите слово «Текущая стоимость» в ячейке A4, а затем введите формулу «= -PV (L2, K1, 0, L3)» в ячейку L
Это должно принести вам 30 695,66 долларов США
Пример текущей стоимости
Скажем, вы вложили деньги в компанию несколько лет назад.Высшее руководство компании хочет вернуть вам 120 000 долларов в год, или вы можете получить деньги сейчас, но это будет 100 000 долларов. Если бы у вас сейчас были 100 000 долларов, вы могли бы инвестировать их с доходностью 5% в течение следующих 12 месяцев. Чтобы определить лучший вариант, вы можете использовать формулу приведенной стоимости:
Чтобы определить лучший вариант, вы можете использовать формулу приведенной стоимости:
PV = 120 000 долларов США / (1 + 0,05) 1
PV = 114 285,71 долларов США
Это означает, что 120 000 долларов США через год стоят 114 285,71 доллара США сегодня, поэтому вы не следует принимать предложение в размере 100 000 долларов США, так как это меньше PV ваших инвестиций.Другими словами, вы должны быть в состоянии ожидать доходности более 5%, чтобы взять 100 000 долларов сегодня вместо 120 000 долларов через год.
Плюсы и минусы приведенной стоимости
Хотя расчет приведенной стоимости важен для определения потенциальной стоимости инвестиций, есть некоторые недостатки. Вот некоторые преимущества и недостатки текущей стоимости.
Преимущества PV
Использование приведенной стоимости — относительно быстрый способ оценить стоимость инвестиций сегодня.Используя калькулятор или Excel, инвесторы могут быстро оценить, стоит ли вкладывать деньги сегодня в конкретный актив при условии стабильной нормы прибыли.
Другими словами, приведенная стоимость — это эффективный способ сравнения инвестиционных решений путем оценки будущих денежных сумм в настоящем.
Недостатки PV
Расчет PV предполагает, что вы можете получить ожидаемую норму прибыли в течение заранее определенного периода времени. Следовательно, приведенная стоимость может вводить в заблуждение.Допустим, вы решили инвестировать в компанию, и норма прибыли меняется каждый год из-за нестабильности в отрасли. В этом случае вычислить приведенную стоимость не так просто, поскольку вы не сможете предсказать реалистичную норму прибыли.
Помните: окупаемость ваших инвестиций не гарантируется, и инфляция также может резко снизить доходность инвестиций.
Текущая стоимость по сравнению с будущей стоимостью
В то время как текущая стоимость рассчитывает, сколько будущая сумма денег стоит сегодня, будущая стоимость смотрит на стоимость текущего актива на заранее установленную дату в будущем на основе предполагаемой нормы прибыли. Формула будущей стоимости также предполагает наличие постоянной нормы прибыли (в дополнение к единственной сумме, вложенной только в начале).
Формула будущей стоимости также предполагает наличие постоянной нормы прибыли (в дополнение к единственной сумме, вложенной только в начале).
Будущая стоимость позволяет инвесторам прогнозировать стоимость различных инвестиций в будущем, тогда как приведенная стоимость показывает, сколько вам нужно сегодня, чтобы заработать определенную сумму денег в будущем.
Текущая стоимость по сравнению с компаундированием
Компаундирование может повлиять на приведенную стоимость, поскольку оно влияет на ставку дисконтирования. При начислении процентов на вложенные деньги начисляются проценты на будущие проценты, помогая увеличить их будущую стоимость.Это означает, что чем чаще начисляется доходность, тем меньше должна быть текущая стоимость будущей суммы для достижения данной будущей стоимости, потому что сложение эффективно увеличивает норму доходности. Точно так же, чем выше коэффициент начисления сложных процентов, тем больше будет будущая стоимость настоящей суммы. При нечастом начислении сложных процентов инвесторам потребуется больше денег сегодня, чтобы заработать ожидаемую будущую стоимость.

 Значение double, обозначающее процентную ставку за период. Например, если вы берете кредит на автомобиль с годовой процентной ставкой, равной 10 %, и ежемесячными выплатами, ставка за период будет равна 0,1/12 (0,0083).
Значение double, обозначающее процентную ставку за период. Например, если вы берете кредит на автомобиль с годовой процентной ставкой, равной 10 %, и ежемесячными выплатами, ставка за период будет равна 0,1/12 (0,0083). Обычно платежи включают основную сумму и проценты, которые не изменяются на протяжении всего периода выплат.
Обычно платежи включают основную сумму и проценты, которые не изменяются на протяжении всего периода выплат. Вариант, определяющий, когда должна производиться выплата. Укажите значение 0, если платежи выплачиваются в конце периода оплаты, или 1, если они выплачиваются в начале периода. Если этот аргумент не задан, используется значение 0.
Вариант, определяющий, когда должна производиться выплата. Укажите значение 0, если платежи выплачиваются в конце периода оплаты, или 1, если они выплачиваются в начале периода. Если этот аргумент не задан, используется значение 0.



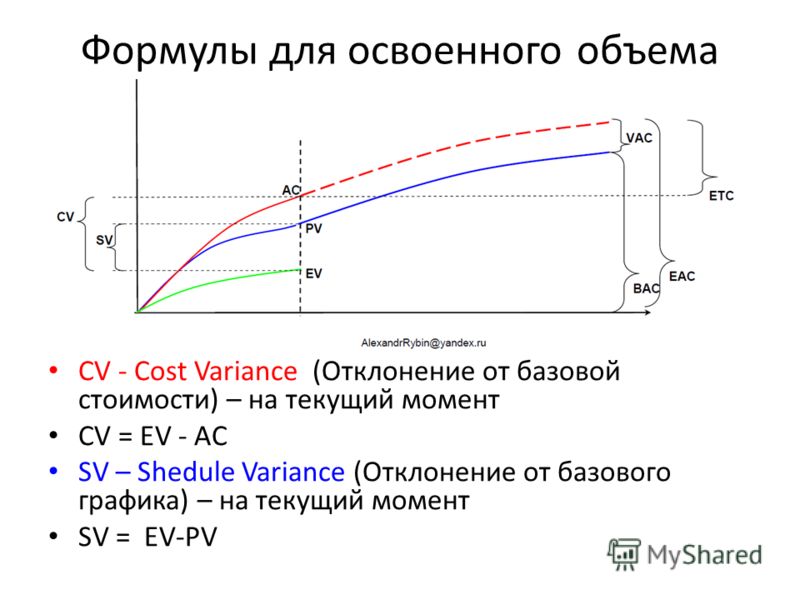 .
.