|
Какова формула для вычисления чистой приведенной стоимости (NPV) в Excel? — 2022
a:Чистая приведенная стоимость (NPV) является основным компонентом корпоративного бюджетирования. Это всеобъемлющий способ рассчитать, будет ли предлагаемый проект обладать добавленной стоимостью или нет.
t с дисконтом со скидкой, r . Сумма всех этих дисконтированных денежных потоков затем компенсируется первоначальной инвестицией, которая равна текущей NPV.
Любая NPV, превышающая $ 0, является проектом с добавленной стоимостью, но в процессе принятия решений между конкурирующими проектами выбирается тот, у которого наибольшая NPV. Одна ложь в этом подходе заключается в том, что, хотя финансово обоснованно с точки зрения теории, расчет NPV только хорош, как данные, управляющие им. Исходя из правильных предположений (затраты на приобретение и удаление, все налоговые последствия, фактический объем и сроки движения денежных средств) чрезвычайно сложны. Вот где большая часть работы действительно имеет место. Если у вас есть данные, их легко подключить. Вычисление NPV в ExcelСуществует два способа расчета NPV в Excel, один из которых использует одну из встроенных формул NPV, вторая — путем разложения денежных потоков компонента и вычисляя каждый шаг индивидуально, затем используя эти вычисления для создания NPV.
 Второй способ предпочтительнее, поскольку лучшие методы финансового моделирования требуют, чтобы вычисления были прозрачными и легко проверяемыми. Проблема с укладкой всех вычислений в формулу состоит в том, что вы не можете легко увидеть, какие числа идут туда, или какие числа являются пользовательскими вводами или жестко закодированы. Другая большая проблема заключается в том, что встроенная формула Excel будет
Второй способ предпочтительнее, поскольку лучшие методы финансового моделирования требуют, чтобы вычисления были прозрачными и легко проверяемыми. Проблема с укладкой всех вычислений в формулу состоит в том, что вы не можете легко увидеть, какие числа идут туда, или какие числа являются пользовательскими вводами или жестко закодированы. Другая большая проблема заключается в том, что встроенная формула Excel будетне чистым из первоначальных денежных средств. Верьте или нет, вам нужно вручную добавить его обратно, если вы использовали встроенную формулу. Вот почему мы рекомендуем и демонстрируем первый подход. Вот простой пример. То, что делает этот пример простым, помимо прочего, заключается в том, что время денежных потоков является как известным, так и согласованным (обсуждается ниже).
Предположим, что компания оценивает рентабельность проекта X. Проект X требует финансирования в размере 250 000 долларов США и, как ожидается, будет генерировать 100 000 долларов США в денежных потоках после налогообложения в первый год, а затем расти на 50 000 долларов США для каждого из следующие четыре года.
Вы можете разбить расписание следующим образом:
[Щелкните правой кнопкой мыши и откройте изображение в новом окне, если трудно прочитать]
Устранения NPV
В приведенном выше примере описаны все этапы, но есть несколько упрощений. Во-первых, предположение, приведенное выше, заключается в том, что все денежные потоки принимаются в единовременной сумме на конец года. Это, безусловно, нереально. В реальном мире не только маловероятно, что вы будете выполнять этот анализ только в конце года, но также маловероятно, что вы получите 100% денежных средств после уплаты налогов в эту дату. (
Узнать больше формул, взяв курс Excel в Excel. ) Правильный метод для исправления первой проблемы заключается в создании коэффициента скин-кода (установите
t, в годах) по количеству времени, прошедшему с момента последнего завершенного года, а вторая проблема исправлена, если предположить, что денежные потоки дисконтируются в середине периода, а не в конце. Это лучше приближает более реалистичное накопление денежных потоков после налогообложения в течение года.
Excel Data Финансовый анализ — CoderLessons.com
Вы можете легко выполнить финансовый анализ в Excel. Excel предоставляет вам несколько финансовых функций, таких как PMT, PV, NPV, XNPV, IRR, MIRR, XIRR и т. Д., Которые позволяют быстро получить результаты финансового анализа.
В этой главе вы узнаете, где и как вы можете использовать эти функции для анализа.
Что такое аннуитет?
Аннуитет — это серия постоянных денежных выплат, осуществляемых в течение непрерывного периода. Например, сбережения на пенсию, страховые выплаты, ипотечный кредит, ипотека и т. Д. В функции аннуитета —
- Положительное число представляет полученные денежные средства.
- Отрицательное число представляет выплаченные деньги.
Приведенная стоимость серии будущих платежей
Приведенная стоимость — это общая сумма, которую сейчас стоит серия будущих платежей. Вы можете рассчитать текущую стоимость с помощью функций Excel —
PV — рассчитывает текущую стоимость инвестиций с использованием процентной ставки и серии будущих платежей (отрицательные значения) и дохода (положительные значения).
 По крайней мере, один из денежных потоков должен быть положительным, и, по крайней мере, один должен быть отрицательным.
По крайней мере, один из денежных потоков должен быть положительным, и, по крайней мере, один должен быть отрицательным.NPV — Расчет чистой приведенной стоимости инвестиций с использованием ставки дисконтирования и серии периодических будущих платежей (отрицательные значения) и дохода (положительные значения).
XNPV — вычисляет чистую приведенную стоимость для графика движения денежных средств, который не обязательно является периодическим.
PV — рассчитывает текущую стоимость инвестиций с использованием процентной ставки и серии будущих платежей (отрицательные значения) и дохода (положительные значения). По крайней мере, один из денежных потоков должен быть положительным, и, по крайней мере, один должен быть отрицательным.
NPV — Расчет чистой приведенной стоимости инвестиций с использованием ставки дисконтирования и серии периодических будущих платежей (отрицательные значения) и дохода (положительные значения).
XNPV — вычисляет чистую приведенную стоимость для графика движения денежных средств, который не обязательно является периодическим.
Обратите внимание, что —
Денежные потоки PV должны быть постоянными, тогда как денежные потоки NPV могут быть переменными.
Денежные потоки PV могут быть в начале или в конце периода, тогда как денежные потоки NPV должны быть в конце периода.
Денежные потоки NPV должны быть периодическими, тогда как денежные потоки XNPV не должны быть периодическими.
Денежные потоки PV должны быть постоянными, тогда как денежные потоки NPV могут быть переменными.
Денежные потоки PV могут быть в начале или в конце периода, тогда как денежные потоки NPV должны быть в конце периода.
Денежные потоки NPV должны быть периодическими, тогда как денежные потоки XNPV не должны быть периодическими.
В этом разделе вы поймете, как работать с PV.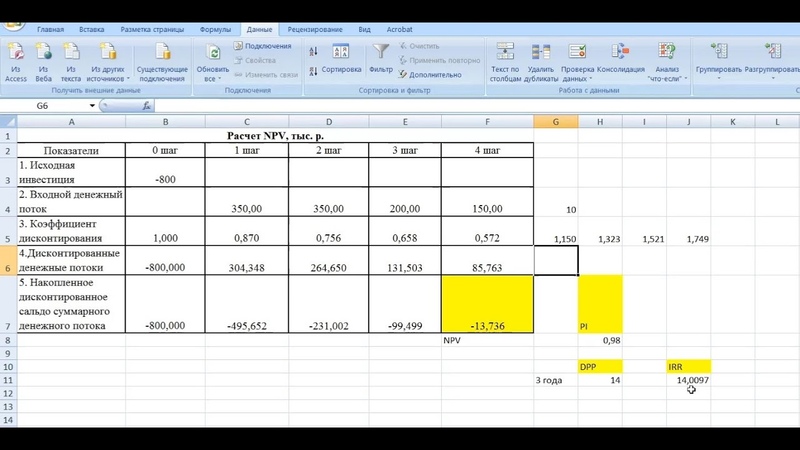 Вы узнаете о NPV в следующем разделе.
Вы узнаете о NPV в следующем разделе.
пример
Предположим, вы покупаете холодильник. Продавец говорит, что цена холодильника составляет 32000, но у вас есть возможность выплатить сумму через 8 лет с процентной ставкой 13% годовых и ежегодными выплатами 6000. У вас также есть возможность совершать платежи. либо в начале или в конце каждого года.
Вы хотите знать, какой из этих вариантов выгоден для вас.
Вы можете использовать функцию Excel PV —
PV (rate, nper, pmt, [fv ], [type])
Чтобы рассчитать текущую стоимость с выплатами в конце каждого года, опустите тип или укажите 0 для типа.
Чтобы рассчитать текущую стоимость с выплатами в конце каждого года, укажите 1 для типа.
Вы получите следующие результаты —
Следовательно,
- Если вы делаете платеж сейчас, вам нужно заплатить 32 000 от текущей стоимости.
- Если вы выбираете ежегодные платежи с оплатой в конце года, вам нужно заплатить 28 793 от приведенной стоимости.

- Если вы выберете ежегодные платежи с оплатой в конце года, вам нужно будет заплатить 32 536 от текущей стоимости.
Вы можете ясно видеть, что вариант 2 выгоден для вас.
Что такое EMI?
Приравниваемый ежемесячный платеж (EMI) определяется Investopedia как «Фиксированная сумма платежа, сделанная заемщиком кредитору на определенную дату каждого календарного месяца. Приравниваемые ежемесячные платежи используются для выплаты процентов и основной суммы каждый месяц, так что в течение По истечении указанного количества лет кредит погашается полностью ».
EMI на займе
В Excel вы можете рассчитать EMI по ссуде с помощью функции PMT.
Предположим, вы хотите взять ипотечный кредит на 5000000 с годовой процентной ставкой 11,5% и сроком кредита на 25 лет. Вы можете найти свой EMI следующим образом —
- Рассчитать процентную ставку в месяц (Процентная ставка в год / 12)
- Рассчитать количество ежемесячных платежей (количество лет * 12)
- Используйте функцию PMT для расчета EMI
Как вы видите,
- Приведенная стоимость (PV) — это сумма кредита.

- Будущая стоимость (FV) равна 0, так как в конце срока сумма кредита должна быть 0.
- Введите 1, поскольку EMI оплачиваются в начале каждого месяца.
Вы получите следующие результаты —
Ежемесячная выплата основной суммы и процентов по кредиту
EMI включает в себя как процентную, так и частичную оплату основного долга. По мере увеличения времени эти два компонента EMI будут меняться, уменьшая баланс.
Получить
Процентная часть ваших ежемесячных платежей, вы можете использовать функцию Excel IPMT.
Оплата основной части ваших ежемесячных платежей, вы можете использовать функцию Excel PPMT.
Процентная часть ваших ежемесячных платежей, вы можете использовать функцию Excel IPMT.
Оплата основной части ваших ежемесячных платежей, вы можете использовать функцию Excel PPMT.
Например, если вы взяли кредит в размере 1 000 000 на срок 8 месяцев по ставке 16% годовых.
Следуйте процедуре, приведенной ниже.
Шаг 1 — Рассчитайте EMI следующим образом.
Это приводит к EMI Rs. 13261,59.
Шаг 2 — Затем рассчитайте проценты и основные части EMI за 8 месяцев, как показано ниже.
Вы получите следующие результаты.
Проценты и основная сумма выплачиваются между двумя периодами
Вы можете рассчитать проценты и основную сумму, выплаченную между двумя периодами включительно.
Вычислите совокупные проценты, выплаченные между 2 и 3 месяцами, используя функцию CUMIPMT.
Проверьте результат, суммируя значения процентов за 2- й и 3- й месяцы.
Вычислите совокупную основную сумму, выплаченную между 2- м и 3- м месяцами, используя функцию CUMPRINC.

Проверьте результат, суммируя основные значения за 2- й и 3- й месяцы.
Вычислите совокупные проценты, выплаченные между 2 и 3 месяцами, используя функцию CUMIPMT.
Проверьте результат, суммируя значения процентов за 2- й и 3- й месяцы.
Вычислите совокупную основную сумму, выплаченную между 2- м и 3- м месяцами, используя функцию CUMPRINC.
Проверьте результат, суммируя основные значения за 2- й и 3- й месяцы.
Вы получите следующие результаты.
Вы видите, что ваши расчеты совпадают с вашими результатами проверки.
Расчет процентной ставки
Предположим, вы берете кредит в размере 100 000 и хотите погасить кредит в течение 15 месяцев с максимальным ежемесячным платежом 12 000. Возможно, вы захотите узнать процентную ставку, по которой вы должны платить.
Найти процентную ставку с помощью функции Excel RATE —
Вы получите результат как 8%.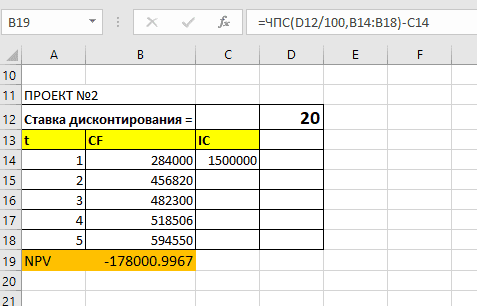
Расчет срока кредита
Предположим, вы берете кредит в размере 100 000 с процентной ставкой 10%. Вы хотите максимальный ежемесячный платеж в размере 15 000. Возможно, вы захотите узнать, сколько времени вам потребуется, чтобы очистить кредит.
Найти количество платежей с помощью функции Excel NPER
Вы получите результат в течение 12 месяцев.
Решения об инвестициях
Когда вы хотите сделать инвестиции, вы сравниваете различные варианты и выбираете тот, который дает более высокую прибыль. Чистая приведенная стоимость полезна для сравнения денежных потоков за определенный период времени и определения того, какой из них лучше. Денежные потоки могут происходить через регулярные, периодические или нерегулярные интервалы.
Сначала рассмотрим случай регулярных периодических денежных потоков .
Чистая приведенная стоимость последовательности денежных потоков, полученных в разные моменты времени в течение n лет (n может быть дробью), составляет 1 / (1 + r) n , где r — годовая процентная ставка.
Рассмотрим следующие две инвестиции в течение 3 лет.
На первый взгляд, Инвестиция 1 выглядит лучше, чем Инвестиция 2. Однако вы можете решить, какая инвестиция лучше, только если вы знаете истинную стоимость инвестиций на сегодняшний день. Вы можете использовать функцию NPV для расчета прибыли.
Денежные потоки могут возникнуть
- В конце каждого года.
- В начале каждого года.
- В середине каждого года.
Функция NPV предполагает, что денежные потоки приходятся на конец года. Если денежные потоки происходят в разное время, необходимо учитывать этот конкретный фактор вместе с расчетом с использованием NPV.
Предположим, что денежные потоки происходят в конце года. Тогда вы можете сразу использовать функцию NPV.
Вы получите следующие результаты —
Как вы видите, NPV для Инвестиции 2 выше, чем для Инвестиции 1. Следовательно, Инвестиция 2 — лучший выбор. Вы получили этот результат, так как потоки вывода средств для Инвестиции 2 относятся к более поздним периодам по сравнению с Инвестициями 1.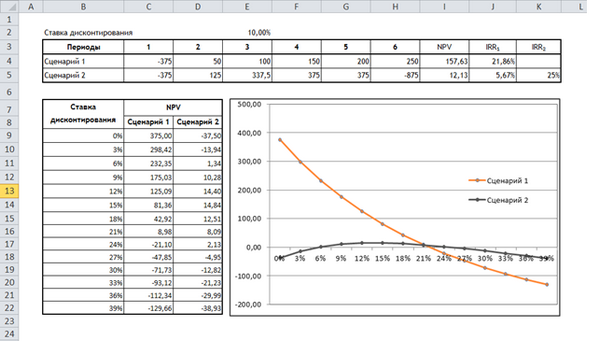
Денежные потоки в начале года
Предположим, что денежные потоки происходят в начале каждого года. В таком случае не следует включать первый денежный поток в расчет NPV, поскольку он уже представляет текущую стоимость. Вам нужно добавить первый денежный поток к NPV, полученному из остальных денежных потоков, чтобы получить чистую приведенную стоимость.
Вы получите следующие результаты —
Денежные потоки в середине года
Предположим, что денежные потоки происходят в середине каждого года. В таком случае вам нужно умножить NPV, полученную из денежных потоков, на $ \ sqrt {1 + r} $, чтобы получить чистую приведенную стоимость.
Вы получите следующие результаты —
Денежные потоки на нерегулярных интервалах
Если вы хотите рассчитать чистую приведенную стоимость с нерегулярными денежными потоками, т.е. денежными потоками, происходящими в случайные моменты времени, вычисление будет немного сложным.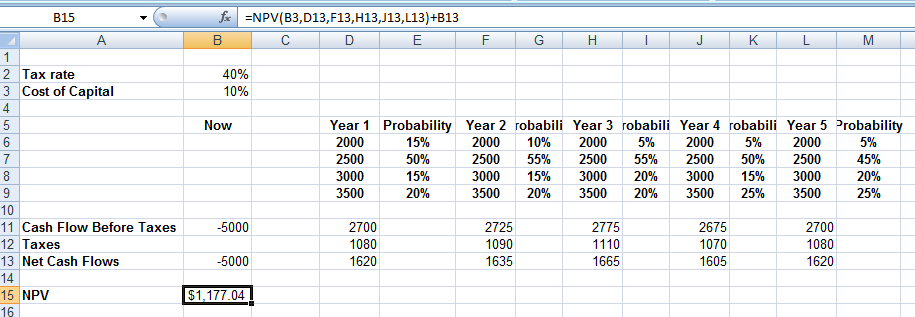
Однако в Excel вы можете легко сделать такой расчет с помощью функции XNPV.
- Упорядочите свои данные с датами и денежными потоками.
Примечание . Первая дата в ваших данных должна быть самой ранней из всех дат. Другие даты могут встречаться в любом порядке.
- Используйте функцию XNPV для расчета чистой приведенной стоимости.
Вы получите следующие результаты —
Предположим, что сегодняшняя дата — 15 марта 2015 года. Как вы заметили, все даты движения денежных средств относятся к более поздним датам. Если вы хотите найти чистую приведенную стоимость на сегодняшний день, включите ее в данные вверху и укажите 0 для денежного потока.
Вы получите следующие результаты —
Внутренняя норма доходности (IRR)
Внутренняя норма доходности (IRR) инвестиции — это процентная ставка, при которой NPV равен 0. Это значение ставки, для которой приведенные значения положительных денежных потоков точно компенсируют отрицательные. Когда ставкой дисконтирования является IRR, инвестиции совершенно безразличны, то есть инвестор не получает и не теряет деньги.
Когда ставкой дисконтирования является IRR, инвестиции совершенно безразличны, то есть инвестор не получает и не теряет деньги.
Рассмотрим следующие денежные потоки, различные процентные ставки и соответствующие значения NPV.
Как вы можете наблюдать между значениями процентной ставки 10% и 11%, знак NPV меняется. Когда вы настраиваете процентную ставку до 10,53%, NPV составляет почти 0. Следовательно, IRR составляет 10,53%.
Определение IRR денежных потоков для проекта
Вы можете рассчитать IRR денежных потоков с помощью функции Excel IRR.
IRR составляет 10,53%, как вы видели в предыдущем разделе.
Для данных денежных потоков IRR может:
- существуют и уникальны
- существует и несколько
- не существует
Уникальный IRR
Если IRR существует и является уникальным, его можно использовать для выбора наилучшей инвестиции среди нескольких возможностей.
Если первый денежный поток отрицателен, это означает, что у инвестора есть деньги и он хочет инвестировать.
 Затем, чем выше IRR, тем лучше, поскольку он представляет процентную ставку, которую получает инвестор.
Затем, чем выше IRR, тем лучше, поскольку он представляет процентную ставку, которую получает инвестор.Если первый денежный поток положительный, это означает, что инвестору нужны деньги и он ищет кредит, чем ниже IRR, тем лучше, поскольку он представляет процентную ставку, которую платит инвестор.
Если первый денежный поток отрицателен, это означает, что у инвестора есть деньги и он хочет инвестировать. Затем, чем выше IRR, тем лучше, поскольку он представляет процентную ставку, которую получает инвестор.
Если первый денежный поток положительный, это означает, что инвестору нужны деньги и он ищет кредит, чем ниже IRR, тем лучше, поскольку он представляет процентную ставку, которую платит инвестор.
Чтобы определить, является ли IRR уникальным или нет, измените значение догадки и рассчитайте IRR. Если IRR остается постоянным, то он уникален.
Как вы заметили, IRR имеет уникальное значение для различных значений догадки.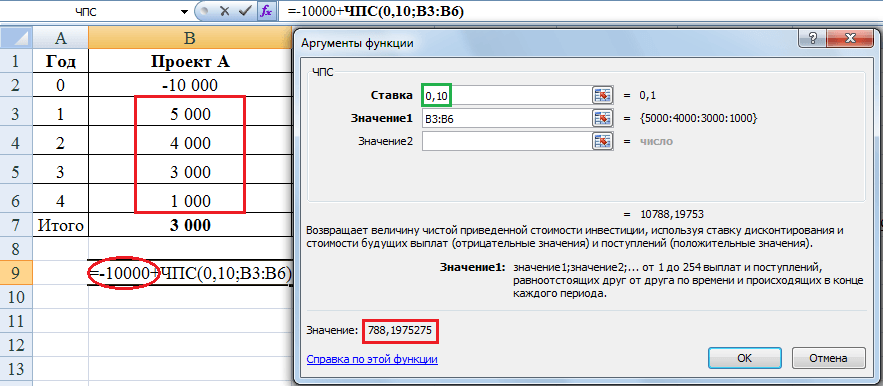
Несколько IRR
В некоторых случаях у вас может быть несколько IRR. Рассмотрим следующие денежные потоки. Рассчитать IRR с различными значениями догадки.
Вы получите следующие результаты —
Вы можете наблюдать, что есть два IRR — -9,59% и 216,09%. Вы можете проверить эти два IRR, вычисляя NPV.
Как для -9,59%, так и для 216,09%, NPV равно 0.
Нет IRR
В некоторых случаях у вас может не быть IRR. Рассмотрим следующие денежные потоки. Рассчитать IRR с различными значениями догадки.
Вы получите результат как #NUM для всех значений догадки.
Результат #NUM означает, что IRR для рассматриваемых денежных потоков отсутствует.
Модели денежных потоков и IRR
Если в денежных потоках есть только один признак изменения, например, с отрицательного на положительный или с положительного на отрицательный, то гарантируется уникальный IRR. Например, в капитальных вложениях первый денежный поток будет отрицательным, а остальные денежные потоки будут положительными.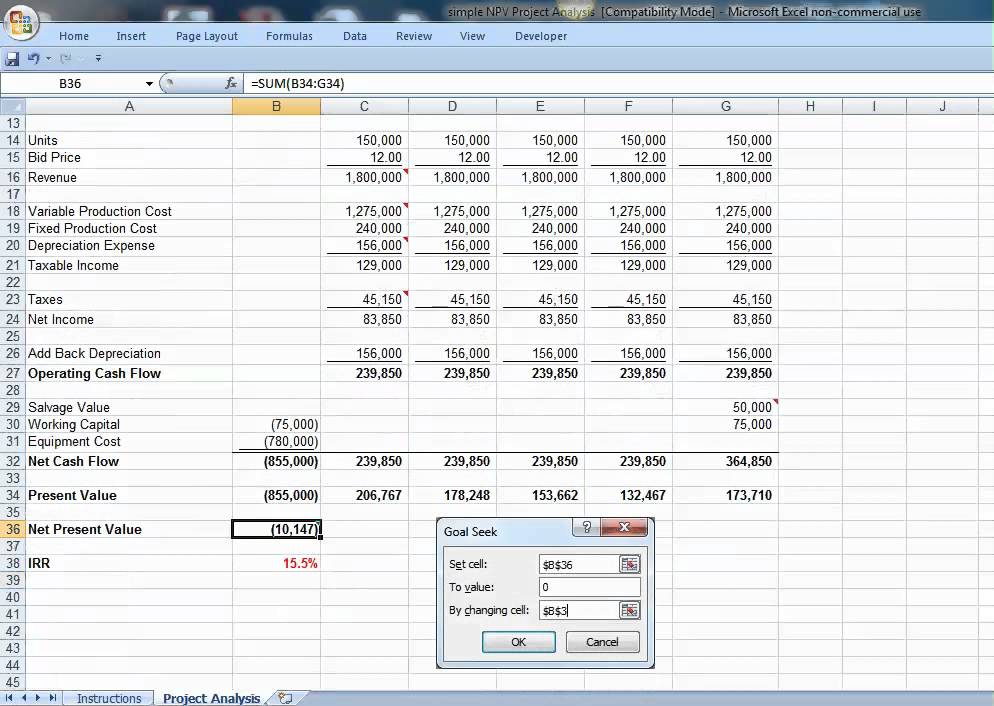 В таких случаях уникальный IRR существует.
В таких случаях уникальный IRR существует.
Если в денежных потоках изменилось более одного знака, IRR может не существовать. Даже если он существует, он не может быть уникальным.
Решения, основанные на IRR
Многие аналитики предпочитают использовать IRR, и это популярный показатель прибыльности, потому что в процентном отношении его легко понять и легко сравнить с требуемым доходом. Тем не менее, есть определенные проблемы при принятии решений с IRR. Если вы ранжируете с IRR и принимаете решения на основе этих рангов, вы можете принять неправильные решения.
Вы уже видели, что NPV позволит вам принимать финансовые решения. Однако IRR и NPV не всегда приводят к одному и тому же решению, когда проекты являются взаимоисключающими.
Взаимоисключающие проекты — это те, для которых выбор одного проекта исключает принятие другого. Когда сравниваемые проекты являются взаимоисключающими, может возникнуть конфликт ранжирования между NPV и IRR. Если вам нужно выбрать между проектом A и проектом B, NPV может предложить принятие проекта A, тогда как IRR может предложить проект B.
Если вам нужно выбрать между проектом A и проектом B, NPV может предложить принятие проекта A, тогда как IRR может предложить проект B.
Этот тип конфликта между NPV и IRR может возникнуть по одной из следующих причин:
- Проекты очень разных размеров, или
- Сроки движения денежных средств разные.
Проекты значительной разницы в размерах
Если вы хотите принять решение с помощью IRR, проект A дает доход 100, а проект B — 50. Следовательно, инвестиции в проект A выглядят выгодно. Однако это неправильное решение из-за разницы в масштабах проектов.
Рассмотрим —
У вас есть 1000, чтобы инвестировать.
Если вы инвестируете все 1000 в проект А, вы получите возврат 100.
Если вы инвестируете 100 в проект B, у вас все еще будет 900, которые вы можете инвестировать в другой проект, скажем, в проект C. Предположим, вы получаете доход в размере 20% по проекту C, а затем общий доход по проекту B и проекту C 230, что значительно опережает рентабельность.

У вас есть 1000, чтобы инвестировать.
Если вы инвестируете все 1000 в проект А, вы получите возврат 100.
Если вы инвестируете 100 в проект B, у вас все еще будет 900, которые вы можете инвестировать в другой проект, скажем, в проект C. Предположим, вы получаете доход в размере 20% по проекту C, а затем общий доход по проекту B и проекту C 230, что значительно опережает рентабельность.
Таким образом, NPV является лучшим способом для принятия решений в таких случаях.
Проекты с разными сроками движения денежных средств
Опять же, если вы считаете, что IRR решит, проект B будет выбором. Тем не менее, проект А имеет более высокую NPV и является идеальным выбором.
IRR нерегулярно расположенных денежных потоков (XIRR)
Ваши денежные потоки иногда могут быть расположены нерегулярно. В таком случае вы не можете использовать IRR, поскольку IRR требует одинаково распределенных временных интервалов. Вместо этого вы можете использовать XIRR, который учитывает даты движения денежных средств вместе с денежными потоками.
Вместо этого вы можете использовать XIRR, который учитывает даты движения денежных средств вместе с денежными потоками.
Внутренняя норма прибыли, которая в результате составляет 26,42%.
Модифицированный IRR (MIRR)
Рассмотрим случай, когда ваша ставка финансирования отличается от вашей ставки реинвестирования. Если вы рассчитываете внутреннюю норму прибыли с IRR, она предполагает одинаковую ставку как для финансирования, так и для реинвестирования. Кроме того, вы также можете получить несколько IRR.
Например, рассмотрим денежные потоки, приведенные ниже —
Как вы заметили, NPV больше 0, чем один раз, что приводит к нескольким IRR. Кроме того, ставка реинвестирования не учитывается. В таких случаях вы можете использовать модифицированный IRR (MIRR).
Вы получите результат 7%, как показано ниже —
Примечание. В отличие от IRR, MIRR всегда будет уникальным.
Что такое чистая приведенная стоимость (NPV) и как ее рассчитать
Опубликовано: 2021-07-01
Многие компании знают, что деньги, которые у них есть, более ценны, чем деньги, которые они ожидают собрать в какой-то момент в будущем. Компании используют деньги, чтобы заработать больше денег, либо покупая товарные запасы и продавая их по более высокой цене, либо инвестируя их для получения прибыли в будущем.
Компании используют деньги, чтобы заработать больше денег, либо покупая товарные запасы и продавая их по более высокой цене, либо инвестируя их для получения прибыли в будущем.
Как вы решаете, в какой момент инвестировать в свой бизнес? По мере расширения компания сталкивается с важными решениями, на которые она должна быстро реагировать, в отношении капиталовложений. К решениям, связанным с расширением бизнеса и огромными капитальными вложениями, следует относиться очень разумно.
Чистая приведенная стоимость (NPV) помогает вам решить, стоили ли ваши инвестиции тратить деньги вашего бизнеса.
В этой статье вы узнаете значение чистой приведенной стоимости (NPV), для чего компании используют NPV, как рассчитать чистую приведенную стоимость с помощью формулы NPV с примерами, как использовать формулу NPV в Excel, типичные ошибки при вычислении и с использованием NPV, отрицательных значений чистой приведенной стоимости и альтернатив, а также чистой приведенной стоимости в сравнении с внутренней нормой доходности.
Давайте начнем.
Что такое чистая приведенная стоимость (ЧПС)?
Чистая приведенная стоимость или сокращенно NPV — это приведенная стоимость денежных потоков при требуемой норме доходности для вашего проекта по сравнению с вложенными вами первоначальными инвестициями. Это относится к методу, используемому для расчета окупаемости инвестиций (ROI) в проект. .
NPV просто смотрит на деньги, которые бизнес ожидает получить от инвестиций, и переводит их в сегодняшнюю денежную стоимость. Компании используют чистую приведенную стоимость, чтобы определить, стоит ли проект того или нет. Это одна из тех основ бухгалтерского учета малого бизнеса, которые должен знать каждый бизнес.
Еще одно богатое определение чистой приведенной стоимости (NPV) состоит в том, что это разница между текущей стоимостью денежных поступлений и денежных потоков за определенный период времени. Это ключевая метрика, используемая для составления бюджета капиталовложений и планирования инвестиций. Чистая приведенная стоимость анализирует прибыльность проекта или предполагаемых инвестиций.
Чистая приведенная стоимость анализирует прибыльность проекта или предполагаемых инвестиций.
Чистая приведенная стоимость (NPV) рассчитывает текущую общую стоимость будущего потока платежей. Он отражает временную стоимость денег, а также используется для сравнения других инвестиционных альтернатив.
Этот ключевой показатель основан на ставке дисконтирования. Эта ставка дисконтирования может быть получена из стоимости капитала, необходимого для инвестиций.
Если чистая приведенная стоимость (ЧПС) инвестиции или проекта положительна, это означает, что дисконтированная приведенная стоимость всех будущих денежных потоков и оттоков, относящихся к этой инвестиции или проекту, также будет положительной. Инвестиции или проекты с отрицательной NPV непривлекательны, и их следует избегать.
Источник: eFinanceManagement.Для чего компании используют NPV?
1. Чтобы убедиться в жизнеспособности проекта или инвестиций
Компании используют чистую приведенную стоимость (NPV), чтобы сравнить проекты или инвестиции и решить, какие из них стоит реализовать. Это помогает компаниям оценить, стоит ли вложение денег.
Это помогает компаниям оценить, стоит ли вложение денег.
Чистая приведенная стоимость — не единственный вариант, доступный для сравнения проектов или инвестиций для компаний и менеджеров, другие варианты включают внутреннюю норму прибыли и метод окупаемости.
Чистая приведенная стоимость (NPV) является предпочтительным выбором большинства финансовых аналитиков для сравнения инвестиций или проектов.
Компании выбирают NPV по двум причинам. Во-первых, он учитывает временную стоимость денег, переводя будущие денежные поступления и оттоки в сегодняшние доллары. Во-вторых, он дает значительное число, которое компании могут использовать для сравнения своих первоначальных инвестиций или денежных затрат с приведенной стоимостью прибыли.
2. Для слияний, поглощений и покупок
Менеджеры используют чистую приведенную стоимость (NPV), чтобы решить, делать ли крупные покупки, такие как программное обеспечение и оборудование. Поскольку капитальные затраты обычно включают значительную сумму денег с выгодой, которая распространяется на долгую перспективу, разумно учитывать чистую приведенную стоимость инвестиций, которые вы хотите приобрести.
Компании также используют его для слияний и поглощений. Когда NPV используется для слияний и поглощений, это называется дисконтированным денежным потоком.
Анализируя и сравнивая различные варианты, вы можете найти наиболее жизнеспособные для инвестирования и те, которых следует избегать или с небольшими или нулевыми перспективами.
Знание того, как рассчитывать и использовать NPV, может помочь компаниям принимать разумные риски, развивать свой бизнес, принимать разумные инвестиционные решения и избегать финансовых трудностей.
Как рассчитать чистую приведенную стоимость по формуле NPV (включая примеры)
Чтобы рассчитать NPV, вам необходимо оценить будущие денежные потоки для каждого периода и определить правильную ставку дисконтирования.
Формула NPV:
NPV = денежный поток / (1 + i) t — первоначальные инвестиции
Где:
i = Требуемый доход или ставка со скидкой
t = количество периодов
Результаты для чистой приведенной стоимости могут быть как положительными, так и отрицательными. Если результат положительный, это показатель того, что проект идеален для инвестиций, а если результат отрицательный, это показатель того, что от него следует отказаться, поскольку это в конечном итоге приведет к утечке денежных средств из компании.
Если результат положительный, это показатель того, что проект идеален для инвестиций, а если результат отрицательный, это показатель того, что от него следует отказаться, поскольку это в конечном итоге приведет к утечке денежных средств из компании.
Чем выше положительный результат чистой приведенной стоимости, тем выгоднее для компании инвестиции или проект.
Что касается ставки со скидкой, важно учитывать, как вы получаете финансирование для проекта. Если вы финансируете за счет ссуд под высокие проценты, учитывайте это при определении чистой приведенной стоимости.
Ставка дисконтирования зависит от компании и от того, как компания получает свои средства. Это либо норма прибыли, которую вы ожидаете получить от своих инвестиций, либо стоимость заимствования денег. Например, если компания ожидает 10% прибыли от инвестиций, она становится ставкой дисконтирования, которую компания использует для расчета своей чистой приведенной стоимости.
Кроме того, если компания должна выплатить 5% процентов по деньгам, которые она заимствовала у финансового учреждения, эта цифра становится дисконтированной ставкой для расчета чистой приведенной стоимости.
Если вы анализируете долгосрочный проект с несколькими денежными потоками, используйте эту формулу.
ЧПС = R t / (1 + i) t
Источник: CleartaxИЛИ
Чистая приведенная стоимость = ∑ Год и общий денежный поток / (1 + ставка дисконтирования ) n
Источник: Harvard Business Review.Если вы не знакомы с двумя предыдущими формулами, вот простой способ рассчитать чистую приведенную стоимость (NPV).
NPV = TVECF — TVIC
куда:
TVECF = сегодняшняя стоимость ожидаемых денежных потоков
TVIC = сегодняшняя стоимость вложенных денежных средств
Пример 1
Поставщик программного обеспечения для бухгалтерского учета участвует в проекте, который стоит 10 000 долларов и генерирует три отдельных денежных потока: 5 000, 3 000 и 8 000 долларов в течение следующих трех лет. Предполагая, что требуемая норма прибыли составляет 10%, какова чистая приведенная стоимость (NPV)?
Предполагая, что требуемая норма прибыли составляет 10%, какова чистая приведенная стоимость (NPV)?
NPV = денежный поток / (1 + i) t — первоначальные инвестиции
Мы можем разбить формулу NPV, чтобы рассчитать каждый денежный поток индивидуально.
NPV = 5000 долларов США / (1 + 0,10) 1 + 3000 долларов США / (1 + 0,10) 2 + 8000 долларов США / (1 + 0,10) 3 — 10 000 долларов США
NPV = 5000 долларов США / 1,10 + 3000 долларов США / 1,21 + 8000 долларов США / 1,331 — 10000 долларов США
NPV = 4545,45 долл. США + 2479,34 долл. США + 6010,52 долл. США — 10 000 долл. США
ЧПС = 3035,31 долл. США
Пример 2
Поставщик программного обеспечения расчета заработной платы рассматривает два потенциальных проектов. Первый проект требует первоначальных инвестиций в размере 20 000 долларов США и, как ожидается, принесет доход в размере 10 000, 8 000 и 15 000 долларов США в течение первых трех лет соответственно при целевой норме доходности 12%.
Второй проект требует первоначальных инвестиций в размере 20 000 долларов США и будет приносить 15 000 долларов США в год в течение двух лет при целевой норме доходности, установленной на уровне 12%. Какова его чистая приведенная стоимость (ЧПС)?
NPV = денежный поток / (1 + i) t — первоначальные инвестиции
NPV для Первого проекта = 10 000 долларов США / (1 + 0,12) 1 + 8 000 долларов США / (1 + 0,12) 2 + 15 000 долларов США / (1 + 0,12) 3 — 20 000 долларов США
NPV для Первого проекта = 10 000 долл. США / 1,12 долл. США + 8 000 долл. США / 1,2544 + 15 000 долл. США / 1,404928 — 20 000 долл. США
NPV для Первого проекта = 8 928,57 долларов США + 6 377,55 долларов США + 10 676,70 долларов США — 20 000 долларов США.
NPV для Первого проекта = 5 982,82 $
Чистая приведенная стоимость первого проекта составляет 5 982,82 доллара США.
NPV для Второго проекта = 15 000 долларов США / (1 + 0,12) 1 + 15 000 долларов США / (1 + 0,12) 2 — 20 000 долларов США
NPV для Второго проекта = 15 000 долл.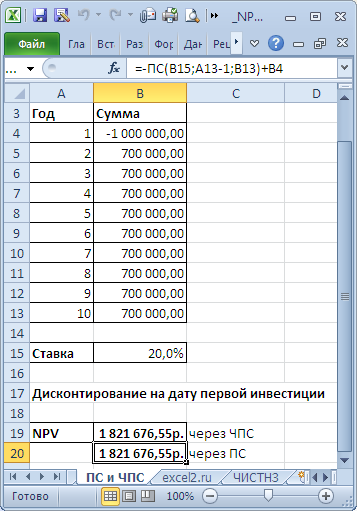 США / 1,12 + 15 000 долл. США / 1,2544 — 20 000 долл. США
США / 1,12 + 15 000 долл. США / 1,2544 — 20 000 долл. США
NPV для Второго проекта = 13 392,86 долларов США + 11 957,91 долларов США — 20 000 долларов США.
NPV для Второго проекта = 5 350,77 долларов США.
Чистая приведенная стоимость второго проекта составляет 5 350,77 долларов США.
Как использовать формулу NPV в Excel?
Вы можете рассчитать чистую приведенную стоимость (NPV) вручную или с помощью калькулятора. Однако эти методы затрудняют расчет чистой приведенной стоимости и подвержены ошибкам. Большинство финансовых аналитиков используют Excel для расчета NPV.
Вот пример того, как использовать функцию чистой приведенной стоимости (NPV) в Excel.
Шаг 1. Установите ставку дисконта в ячейке.Шаг 2: Создайте серию денежных потоков (должны быть в последовательных ячейках).Шаг 3: Введите «= ЧПС (« и выберите ставку дисконтирования », затем выберите ячейки движения денежных средств и«) ».
Распространенные ошибки при вычислении и использовании NPV
1. Трудно объяснить другим
Наиболее очевидная проблема при расчете и использовании чистой приведенной стоимости (NPV) заключается в том, что ее трудно объяснить другим. Дисконтированная стоимость будущих денежных потоков — это не фраза, которая имеет большое значение для тех, кто не знаком с бухгалтерским учетом.
Несмотря на трудности с объяснением чистой приведенной стоимости другим, стоит приложить дополнительные усилия, чтобы объяснить ее, поскольку она выгодна для компаний и акционеров.
Любая инвестиция, прошедшая тест NPV, скорее всего, увеличит стоимость инвестиций компании или акционера. Любая инвестиция, не прошедшая тест NPV (имеющая отрицательное значение), нанесет ущерб инвестициям компании и акционера.
2. Основано на нескольких предположениях и оценках
Чистая приведенная стоимость (NPV) основана на нескольких предположениях и оценках, которые оставляют много места для ошибок, если вы не будете осторожны.
Двойная проверка расчета NPV может помочь снизить риски совершения ошибок. Вы также можете выполнить анализ чувствительности после того, как рассчитали первоначальный расчет NPV.
Есть три области, в которых вы больше всего рискуете ошибиться при расчете чистой приведенной стоимости. Неправильная оценка по цифре в любой из этих областей сильно повлияет на результаты расчета NPV.
Первое направление — это первоначальные вложения. Если вы покупаете оборудование с четкой ценой, легко узнать свои первоначальные вложения.
Однако, если вы обновляете свою бизнес-систему для использования системы ERP, вы легко можете ошибиться из-за разницы в стоимости.
Вторая область — это учетная ставка. Существует большой риск использования сегодняшней ставки дисконтирования для расчета вашей будущей прибыли, особенно если она не зафиксирована. Ставка дисконтирования на первый год может быть не такой же, как на третий год проекта.
Процентные ставки, если вы взяли ссуду, могут резко подскочить, что приведет к увеличению ваших расходов. Это означает, что ваши предполагаемые доходы за этот год будут меньше, чем вы изначально рассчитали.
Это означает, что ваши предполагаемые доходы за этот год будут меньше, чем вы изначально рассчитали.
Третья область, в которой компании делают ошибки при расчете и использовании чистой приведенной стоимости (NPV), — это оценка предполагаемой доходности вашего прогноза.
3. Дисконтирование нулевых инвестиций
Нулевое время — это номинальная или реальная стоимость ваших инвестиций, поэтому нет необходимости ее дисконтировать. Однако нередки случаи, когда компании или частные лица случайно сбрасывают со счетов нулевую сумму инвестиций.
Поскольку нулевая сумма инвестиций представляет собой денежные вложения, и это всегда отрицательный денежный поток, ее преднамеренное или случайное дисконтирование означает, что вы уменьшаете размер или стоимость своих инвестиций. Это также означает, что вы дважды дисконтируете положительные денежные потоки будущего периода.
Опасность дисконтирования инвестиций с нулевым моментом времени состоит в том, что вы сделаете чистую приведенную стоимость (NPV) вашего проекта ниже, чем она есть на самом деле.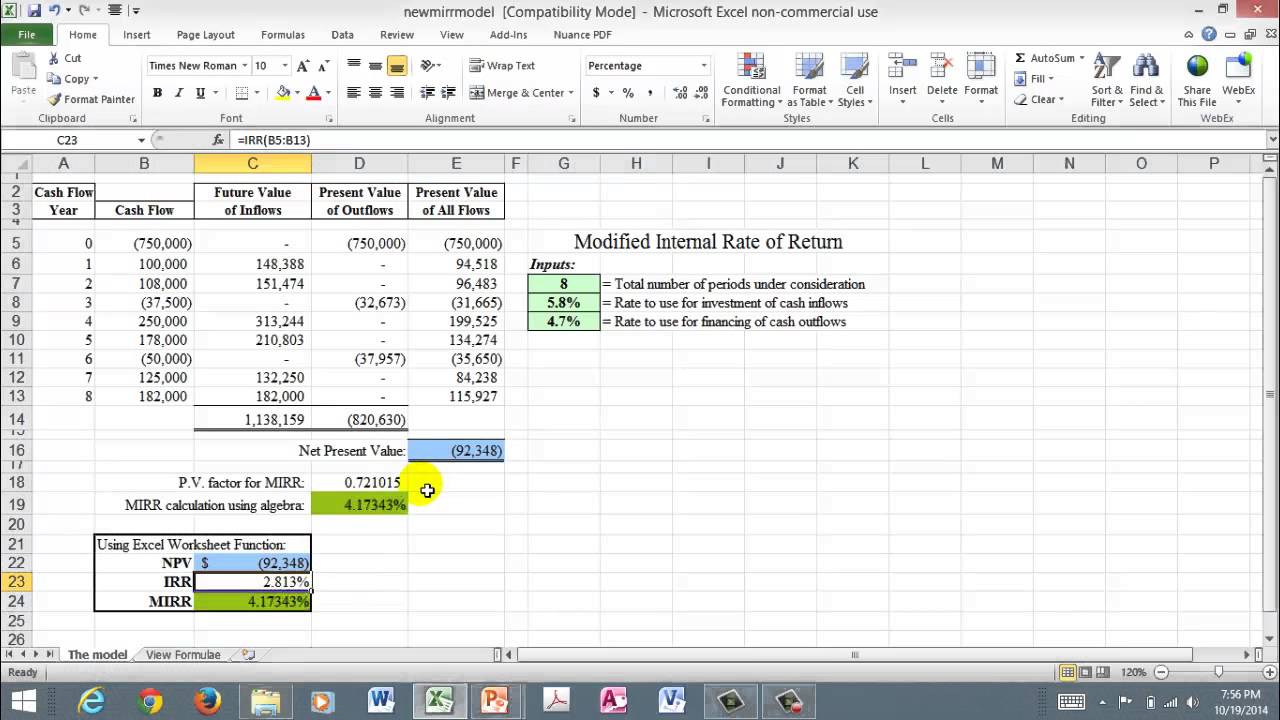
Чтобы избежать введения в заблуждение чистой приведенной стоимости, не сбрасывайте нулевое значение времени при вычислении формулы NPV вручную, с помощью калькулятора или Excel. Единственные значения, которые вы должны сбрасывать со счетов, — это будущие и ненулевые значения.
Недостатки чистой приведенной стоимости и альтернативы
Бизнес-аналитики используют чистую приведенную стоимость (NPV) для оценки прибыльности инвестиций. NPV в значительной степени зависит от оценок и предположений, которые могут оставлять место для ошибок. Предполагаемые факторы, такие как ставка дисконтирования, инвестиционные затраты и прогнозируемая доходность, подвержены ошибкам, если не будут рассчитаны тщательно.
Для начала проекта могут потребоваться непредвиденные расходы или дополнительные расходы в конце проекта, что может привести к неточности рассчитанной чистой приведенной стоимости (NPV).
Хотя чистая приведенная стоимость (NPV) является ключевым показателем, используемым компаниями и бухгалтерами для определения рентабельности инвестиций (ROI), она имеет свою долю недостатков.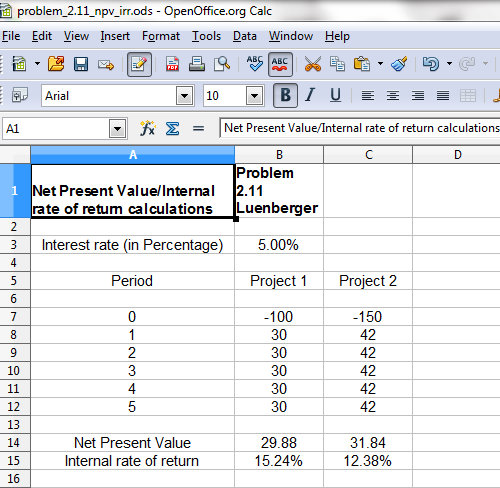
Причина, по которой существует так много места для ошибок при расчете чистой приведенной стоимости, заключается в том, что расчеты основаны на обоснованных оценках. Эти оценки основаны на прошлых и текущих расходах.
При расчете чистой приведенной стоимости вы должны учитывать правильность оценки проекта или инвестиций. Точность проекта или инвестиций зависит от текущих рыночных условий, возможности тарифов, потенциала роста цен и потенциала перерасхода средств.
При покупке оборудования по определенной цене чистую приведенную стоимость легко рассчитать, поскольку вариантов не так много. Однако проблемы возникают, когда вы имеете дело с проектом или инвестициями, реальная стоимость которых варьируется.
Еще один недостаток использования чистой покупной стоимости заключается в том, что ставка дисконтирования может не отражать то, что произойдет в будущем. Изменения на рынке, вызванные спросом, предложением и другими факторами, могут либо помешать, либо стать огромным преимуществом для чистой прибыли.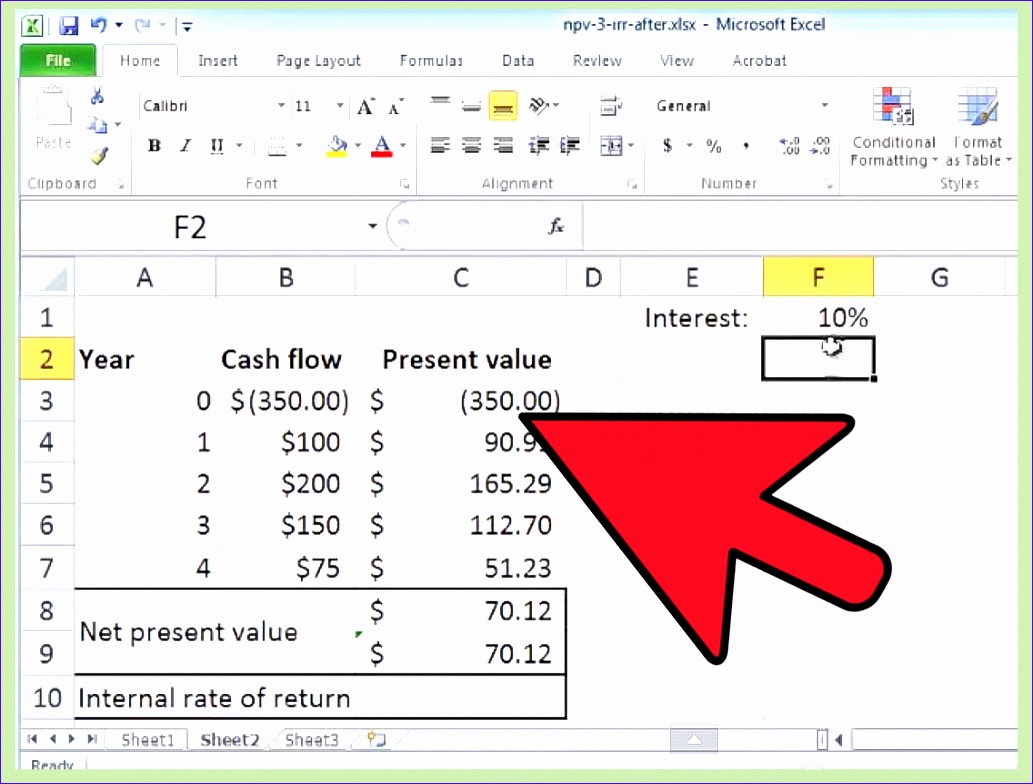
Рентабельность инвестиций (ROI)
Рентабельность инвестиций (ROI) — это альтернатива чистой приведенной стоимости (NPV), которая измеряет прибыльность инвестиций. Компании используют показатель рентабельности инвестиций (ROI), чтобы решить, куда инвестировать свою прибыль.
Формула расчета рентабельности инвестиций (ROI):
ROI = (Чистая прибыль / Стоимость инвестиций) x 100
Источник: WallStreetMojoКомпании используют ROI для измерения рентабельности своего бизнеса, активов и определения прибыли от инвестиций в акции компании. Он измеряет прибыль от инвестиций относительно стоимости инвестиций.
Например, если компания инвестирует в виртуальную телефонную систему за 1500 долларов и продает ее позже за 2000 долларов. Какова его рентабельность инвестиций (ROI)?
ROI = (Чистая прибыль / Стоимость инвестиций) x 100
Чистая прибыль = Общий доход от инвестиций — Стоимость инвестиций
Чистая прибыль = 2000 — 1500 долларов
Чистая прибыль = 500 $
Рентабельность инвестиций = (500 долл. США / 1500 долл. США) x 100
США / 1500 долл. США) x 100
Рентабельность инвестиций = 33,33%
Срок окупаемости
Срок окупаемости или метод окупаемости является альтернативой чистой приведенной стоимости (NPV). Он рассчитывает, сколько времени нужно для возврата первоначальных инвестиций. Он строго ограничен тем, сколько времени потребуется для создания начальных инвестиционных затрат.
Проблема с использованием периода или метода окупаемости заключается в том, что они не учитывают временную стоимость денег. В связи с этим использование сроков окупаемости для расчета долгосрочных инвестиций может быть неточным. Также сравнения по срокам окупаемости не учитывают долгосрочную доходность вложений.
Формула расчета срока окупаемости:
Срок окупаемости = первоначальные инвестиции / годовой приток денежных средств
Источник: Commerce Study Guide.Чистая приведенная стоимость против внутренней нормы прибыли
Чистая приведенная стоимость и внутренняя норма прибыли используют денежный поток в качестве основы для измерения эффективности инвестиций. Они оба учитывают временную стоимость денег, предлагают четкую основу для принятия решений и используют финансовые цели и планы, основанные на субъективных предположениях.
Они оба учитывают временную стоимость денег, предлагают четкую основу для принятия решений и используют финансовые цели и планы, основанные на субъективных предположениях.
Вот различия между чистой приведенной стоимостью и внутренней нормой доходности.
1. Значение
Чистая приведенная стоимость (NPV) относится к приведенной стоимости денежных потоков при требуемой норме доходности для вашего проекта по сравнению с вложенными вами первоначальными инвестициями. Внутренняя норма доходности (IRR) относится к ставке, при которой денежные поступления равны денежный отток. IRR — ключевой показатель
2. Представительство
Внутренняя норма доходности (IRR) представлена в процентах, а чистая приведенная стоимость (NPV) представлена в абсолютном выражении.
3. Что они обозначают
Чистая приведенная стоимость указывает на прибыль от проекта или инвестиций, в то время как внутренняя норма прибыли — это точка безубыточности проекта или инвестиций, при которых нет убытков или прибыли.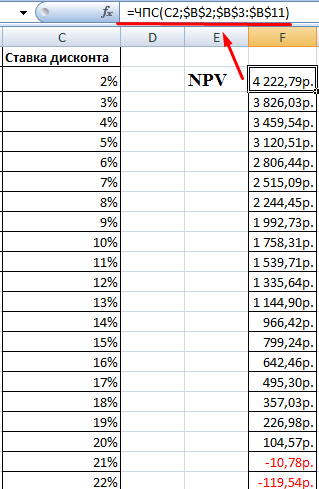
4. Ставка на реинвестирование
Чистая приведенная стоимость использует стоимость капитала в качестве ставки для реинвестирования, в то время как IRR использует внутреннюю норму прибыли в качестве ставки для реинвестирования.
5. Переменный отток денежных средств
Переменный отток денежных средств по-разному влияет на NPV и IRR. Это не влияет на NPV, но приводит к отрицательной или множественной IRR.
Источник: eFinancialModelsЧасто задаваемые вопросы о чистой приведенной стоимости
Что означает чистая приведенная стоимость?Чистая приведенная стоимость (ЧПС) определяется как приведенная стоимость ряда денежных потоков после дисконтирования требуемой для инвестора нормы прибыли. Это результат вычислений, используемых для определения приведенной стоимости будущего потока платежей с учетом временной стоимости денег.
Финансовые аналитики используют его как инструмент анализа, чтобы решить, стоит ли рисковать.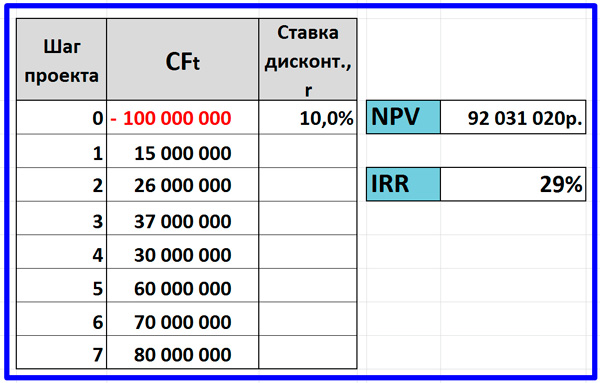
IRR — это внутренняя норма доходности. IRR оценивает прибыльность потенциальных инвестиций, используя процентное значение, а не сумму в долларах, и часто не учитывает внешние факторы, такие как инфляция.
NPV, с другой стороны, использует не процентное значение, а сумму в долларах и учитывает внешние факторы, такие как инфляция.
Почему NPV лучше IRR?Преимущество использования метода NPV по сравнению с IRR заключается в том, что NPV может работать с несколькими ставками дисконтирования в долгосрочной перспективе без каких-либо проблем .
Если аналитик оценивает один проект или несколько проектов, которые имеют общую ставку дисконтирования и денежные потоки, IRR будет работать. Но это становится очень неэффективным, когда эти проекты рассчитываются на долгосрочную перспективу и не имеют одинаковых ставок дисконтирования и денежных потоков.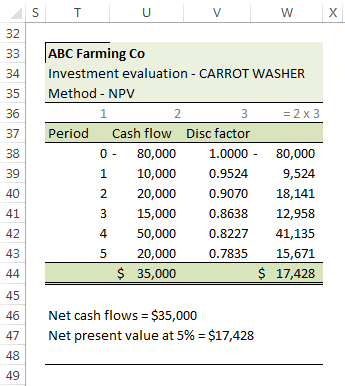
NPV, с другой стороны, позволяет дисконтировать денежный поток каждого года отдельно от других, что делает NPV лучшим методом.
Почему дисконтируются будущие денежные потоки?Будущие денежные потоки необходимо дисконтировать из-за теории временной стоимости денег. Временная стоимость денег (TVM) — это концепция, согласно которой деньги, которые у вас есть сейчас, стоят больше, чем такая же сумма в будущем, из-за их потенциальной доходности.
Это означает, что с учетом процентной ставки 10 000 долларов через год не будут стоить столько, сколько 10 000 долларов сегодня. Например, если через год при процентной ставке 5% у вас будет 10 500 долларов, значит, ваши деньги сохранят свою покупательную способность. Что-нибудь меньшее, и оно потеряет свою ценность.
Что это значит, если NPV = 0? Нулевое значение NPV означает, что приток денежных средств по проекту в точности эквивалентен оттоку денежных средств. Средства, вложенные в проект, приносят доход по этой процентной ставке, что означает, что инвестор не станет ни богаче, ни беднее по прошествии расчетного времени.
Средства, вложенные в проект, приносят доход по этой процентной ставке, что означает, что инвестор не станет ни богаче, ни беднее по прошествии расчетного времени.
С финансовой точки зрения это не выглядит привлекательным вложением, но бывают ситуации, когда прибыль не является основной целью проекта, поэтому нулевой NPV является приемлемым.
Оценка инвестиционных проектов с применением MsExcel
Программа
1. Теоретические основы инвестиционных проектов. Виды, классификации инвестиций.
2. Концепция временной стоимости денег. Текущая стоимость (PV), будущая стоимость (FV). Простые и сложные проценты. Ставка дисконтирования. Аннуитет. Prenumerando, postnumerando.
3. Денежный поток. Классификации ДП. ДП от текущей, инвестиционной и финансовой деятельности. ЧДП, настоящий и будущий денежные потоки.
4. Оценка финансовых инвестиций. Государственные и корпоративные облигации. Текущая стоимость облигаций (консольные, купонные с конечным сроком погашения, бескупонные с конечным сроком пога-шения). Акции (привилегированные, с потоком дивидендов, с постоянным темпом прироста дивидендов).
Акции (привилегированные, с потоком дивидендов, с постоянным темпом прироста дивидендов).
5. Принципы и схема оценки инвестиционных проектов. Статические и динамические методы (NPV, PI, IRR, PBP. Точка Фишера).
6. Риск и доходность. Безрисковый эквивалент СЕ (certainly equivalent). Ожидаемая доходность. Риск ожидаемой доходности — СКО, вариация. Модель Шарпа для оценки доходности акции. Характеристическая линия. Модель арбитражного ценообразования (Фама, Росс).
7. Методология оценки инвестиционных проектов: компьютерный практикум. Программный продукт MS Excel. Оценка будущих и приведенных сумм инвестиций, платежей ренты. Расчеты с учетом инфляции. Применение MS Excel для расчета инвестиционных проектов. Функции MS Excel: ПС (PV), БС (FV), ПЛТ (PMT), ЧПС (NPV), ВСД (IRR). Особенности их применения. Вычисление размера погашающего платежа с разделением на части (выплаты по процентам и по основному долгу). Функции MS Excel: ПРПЛТ и ОСПЛТ. Оценка инвестиционных проектов, денежные потоки которых не носят периодиче-ский характер. Функции MS Excel: ЧИСТНЗ и ЧИСТВНДОХ.
Функции MS Excel: ЧИСТНЗ и ЧИСТВНДОХ.
8. Риск инвестиционного проекта. Дерево вероятностей. Начальная, условная, совместная вероятности. Ожидаемое NPV. СКО и вариация NPV. Метод Монте-Карло. Расчеты в Excel.
9. Неопределенность и риск. Виды рисков. Показатели доходности и риска при инвестировании в ценные бумаги. Риск инвестиций. Измерение риска. Соотношение доходности и риска. Расчеты в Excel.
10. Инвестиционные портфели. Принцип формирования инвестиционных портфелей. Доходность и риск инвестиционного портфеля. Теория диверсификации Марковица. Определение оптимального инвестиционного портфеля. Расчеты в Excel.
11. Оптимизация инвестирования. Использование концепции рисковой стоимости (Value at Risk – VAR) для оценки эффективности инвестиционных проектов. Модели и критерии оптимального отбора. Сравнение инвестиционных проектов разной продолжительности. Критические точки и анализ чувствительности инвестиционного проекта. Метод сценариев. Моделирование и прогнозирование денежных потоков по проекту. Итоговый СaseStudy на персональных компьютерах.
Итоговый СaseStudy на персональных компьютерах.
Компетенции
приобретение слушателями компетенций в области теории и практики оценки инвестиций и управленческих решений в рамках инвестиционной деятельности и применение различных методик расчета экономической эффективности инвестиционного проекта. Приобретение слушателями специальных знаний, умений и навыков, необходимых для работы в сфере оценки инвестиций.
Финансовые модели — Сергей Черемушкин
Внимание! Модели сделаны в MS Excel 2013. Некоторые функции могут не работать в более ранних версиях.
Payback Period of a Nonconventional Cash Flow
PowerPivot
Ссылка на видео
Интерполяция
Линейная интерполяция (видео)
Полиномиальная интерполяция методом Лагранжа (видео)
Полиномиальная интерполяция методом Ньютона (видео)
Признание выручки по долгосрочному договору в соответствии с IFRS 15 (на примере строительной организации)
Показан порядок расчета underbillings и overbillings.
Модели терминальной стоимости с заемным финансированием
Распространенный на практике и в учебной литературе способ пересчета терминальной стоимости на конец периода в стоимость в нулевой момент времени по ставке WACC приводит к неправильным результатам. В рабочей книге рассмотрены основные ошибки и показан правильный способ пересчета терминальной стоимости. Представлены шаблоны трех моделей терминальной стоимости: с неизменной абсолютной величиной долга, с целевой рыночной структурой капитала и с целевой балансовой структурой капитала.
Модели займов и кредитов
Шаблон расчета точки безубыточности многопродуктовой фирмы
Расчет срока окупаемости инвестиционного проекта
Простейший пример алгоритма приведения в равновесие прогнозных финансовых отчетов
Модели основных средств и амортизации для прогнозных финансовых отчетов
Пример оптимизационной модели отбора инвестиционных проектов по критерию NPV
Внимание! Файлы открываются в программе AIMMS.
Примеры расчета свободного денежного потока фирмы и свободного денежного потока собственникам
Прогноз урожайности зерновых культур
Пример дисконтирования денежных потоков с использованием изменяющихся во времени ставок дисконтирования
Представленная модель демонстрирует расчет стоимостных показателей результативности инвестиционного проекта на основе конечных денежных потоков. Традиционный метод дисконтирования свободного денежного потока фирмы (проекта) FCFF по неизменной во времени ставке WACC и свободного денежного потока собственникам FCFE по неизменной во времени ставке CoLE не пригоден для анализа конечных денежных потоков, поскольку содержит допущение о неизменной абсолютной величине долга или неизменной структуре капитала и иные нереалистичные допущения (например, допущение о безрисковом долге). В случае конечных денежных потоков ставки WACC и CoLE изменяются во времени вместе с изменением соотношения между денежным потоком фирмы и денежным потоком по долгу.
Представленная модель раскрывает правильную методологию оценки стоимости проекта с позиций ключевых стейкхолдеров методом дисконтирования по компонентам, позволяющим использовать изменяющиеся во времени ставки дисконтирования. Для сравнения также представлены расчеты дисконтирования денежного потока нелевериджированной фирмы (CFF), денежного потока левериджированной фирмы (CCF) и денежного потока собственникам (CFE) с использованием исправленных формулировок ставок дисконтирования WACCCFF, WACCCCF и CoLE.
«Штопор» и примеры его применения
Ссылка на видео
Как рассчитать NPV в Excel
- Руководство по карьере
- Развитие карьеры
- Как использовать функцию Excel NPV
30 декабря 2021 г. который говорит людям, будет ли проект прибыльным. Это основополагающая концепция корпоративных финансов, на которую полагаются компании для точного прогнозирования.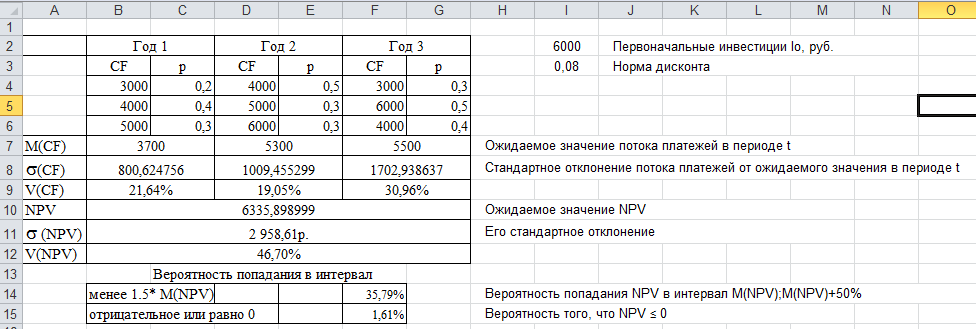 По этой причине знание того, как рассчитать NPV в Excel, может быть важной частью работы финансового специалиста.В этой статье мы обсудим NPV и как его рассчитать.
По этой причине знание того, как рассчитать NPV в Excel, может быть важной частью работы финансового специалиста.В этой статье мы обсудим NPV и как его рассчитать.
Что такое чистая приведенная стоимость
чистая приведенная стоимость является основным расчетом для всех предприятий. Это важный инструмент финансового моделирования, используемый для ряда отчетов и значений, включая отчеты о движении денежных средств, ставку дисконтирования для проекта, конечную и ликвидационную стоимость и многое другое. Он используется для определения прибыльности и имеет значение для ряда важных финансовых процессов.
В целях финансового моделирования чистая приведенная стоимость имеет жизненно важное значение для успеха в бизнесе.Это связано с тем, что это упрощенное значение, которое может с первого взгляда сказать заинтересованным сторонам, является ли проект прибыльным. Именно по этой причине многие люди обращаются к Excel, чтобы создать формулу, которая быстро выполняет расчеты чистой приведенной стоимости, что может потребоваться профессионалам в области финансов.
Формула NPV, которая позволяет математикам вычислять ее вручную, выглядит так, хотя большинство людей не делают ее так:
В этом сценарии NPV, конечно же, означает чистую приведенную стоимость. «F» — это будущие денежные потоки, «i» — процентная ставка, а «n» — количество финансовых периодов до тех пор, пока денежный поток не будет реализован.
Поскольку многие люди не являются математиками или статистиками, а обученные финансовые специалисты всегда ищут способы эффективной работы, многие люди обращаются к Excel для выполнения этой функции без каких-либо математических расчетов. В Excel использование функции NPV преобразует необработанные данные, введенные в электронную таблицу, в пригодную для использования NPV, которая может быть определяющим фактором в отношении того, сможет ли компания взяться за проект и остаться прибыльной.
Таким образом, NPV — это математическая формула, но также и функция Excel со следующим синтаксисом:
=NPV (ставка, [значение1], [значение2], [значение 3].
 ..)
..)
Многим специалистам полезно научиться рассчитывать чистую приведенную стоимость в Excel. Вот почему важно понимать, что существует более одного способа расчета.
Связано: Узнайте, как стать финансовым менеджером
Как компании используют NPV
Чтобы лучше понять, как компании используют NPV, давайте рассмотрим пример:
Компания Elastic Micro открывает новый склад, для которого требуются первоначальные инвестиции в размере 150 000 долларов США. Поскольку склад новый, первоначальные инвестиции учитываются как расходы в размере 150 000 долларов США или -150 000 долларов США.Это вычет из первоначальных затрат, и, поскольку компания не произвела никакой продукции в первый год развития склада, он также отражается как отрицательная прибыль. Когда это происходит, предприятия, как правило, уже наметили, какой они ожидают свою будущую прибыль. Это стандартная часть процесса бизнес-планирования.
Например, скажем, прибыль Elastic Micro Company в первый год от новых инвестиций составляет -150 000 долларов, поскольку фабрика еще не начала приносить прибыль. Однако во второй год они ожидают получить прибыль в размере 100 000 долларов, а в год 3 — 150 000 долларов, и прибыль будет расти с шагом 50 000 долларов из года в год в течение пяти лет прогнозов, пока не достигнет 250 000 долларов.
Однако во второй год они ожидают получить прибыль в размере 100 000 долларов, а в год 3 — 150 000 долларов, и прибыль будет расти с шагом 50 000 долларов из года в год в течение пяти лет прогнозов, пока не достигнет 250 000 долларов.
Чистая текущая стоимость определяет прибыльность проекта с помощью сложной формулы, которая учитывает эти будущие ожидаемые прибыли, сводя все денежные потоки к одному моменту времени. Когда это происходит, финансовые аналитики определяют «приведенную стоимость», которая является отличительной чертой методологии NPV.Эта финансовая модель утверждает, что если NPV является положительным числом, проект будет положительным, но если это не так, проект также не будет прибыльным.
В этом примере относительно легко увидеть, что компания возместит первоначальные инвестиции в течение 3 лет своей деятельности. Однако для многих компаний, которые имеют более сложные бухгалтерские и финансовые соображения, цифры не так легко понять, просто взглянув на несколько прогнозов.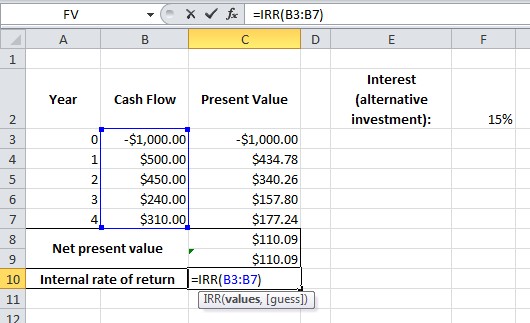 Вот где NPV важна для быстрого принятия бизнес-решений.
Вот где NPV важна для быстрого принятия бизнес-решений.
Связано: Узнайте, как стать специалистом по финансовому планированию
Как рассчитать чистую приведенную стоимость в Excel
Excel — важный корпоративный бизнес-инструмент, на который полагаются финансовые специалисты для расчета цифр, хранения данных и создания отчетов вручную, адаптированных к индивидуальному бизнесу. Популярное программное обеспечение для работы с электронными таблицами имеет функцию, предназначенную для расчета чистой приведенной стоимости. Использование Microsoft Excel вместо выполнения вычислений вручную устраняет некоторые из более сложных шагов, позволяя предприятиям быстро находить их.Вот как рассчитать NPV в Excel:
Поймите синтаксис.
Выберите ячейку для представления NPV.
Спроектируйте будущие денежные потоки и установите процентную ставку.
Рассчитать.
1. Понимание синтаксиса
Синтаксис, используемый для вызова NPV из Excel: =NPV (скорость, [значение1], [значение2], [значение 3]. ..). В этой формуле ставка выражена в процентной ставке, а значения представляют собой будущие денежные потоки.
..). В этой формуле ставка выражена в процентной ставке, а значения представляют собой будущие денежные потоки.
Рассматривая тот же пример для компании Elastic Micro, предположим, что процентная ставка по инвестициям составляет 7%. Следовательно, = NPV(7%, -[150 000 долл. США], [100 000 долл. США], [150 000 долл. США], [200 000 долл. США], [250 000 долл. США]).
2. Выберите ячейку для представления NPV
Как только вы поймете синтаксис, вы должны найти ячейку на листе и обозначить ее для NPV. Это ячейка, в которую вы вернетесь, чтобы ввести свой синтаксис.
3. Спрогнозируйте будущие денежные потоки и установите процентную ставку
Вам потребуется ввести прогнозируемые денежные потоки в ряд последовательных ячеек и выделить ячейку для процентной ставки.Заполните все эти установленные ячейки необходимой важной информацией. В этом случае у нас будет ячейка для процентной ставки 7% и пять последовательных ячеек в строке, которые созданы для ввода будущих значений прогнозируемой прибыли, которые уже были рассчитаны.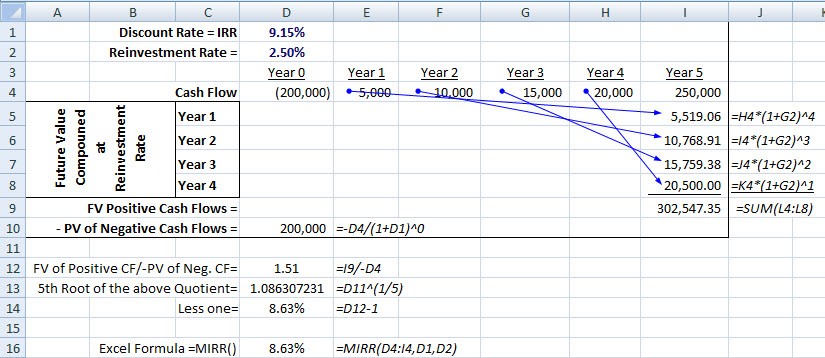
Связано: Ваше руководство по карьере в сфере финансов
4. Рассчитайте
Со всей информацией, необходимой для расчета чистой приведенной стоимости, указанной в электронной таблице Excel, вернитесь к ячейке, которую вы хотите ввести в синтаксисе.Введите «=NPV([выберите ячейку с процентной ставкой], [выделите каждую ячейку с будущей прибылью, поставив между ними запятую])». В этом случае чистая приведенная стоимость составляет 400 427,23 доллара. Этот проект прибыльный.
Как рассчитать NPV в Excel (чистая приведенная стоимость)
При работе с данными, связанными с инвестициями и оценкой проектов, иногда может потребоваться вычислить NPV (чистую текущую стоимость) проектов/инвестиций.
В этом уроке я покажу вам, как рассчитать чистую текущую стоимость (NPV) в Excel, используя две простые встроенные функции (NPV и XNPV).
Итак, приступим!
Что такое NPV – простое объяснение
Давайте сначала разберемся, что означает чистая приведенная стоимость.
NPV — это значение, которое представляет текущую стоимость всех будущих денежных потоков без учета первоначальных инвестиций . Другими словами, вы можете узнать стоимость будущих доходов, приведенных к текущей стоимости.
Поясню на примере.
Предположим, у вас есть проект, в который вам нужно инвестировать 50 000 долларов сейчас, и он будет приносить вам 10 000 долларов каждый год в течение следующих 10 лет.
Учитывая, что вы знаете преобладающую ставку дисконтирования (также называемую процентной ставкой стоимости капитала), вы можете рассчитать, сколько сейчас стоят эти деньги (которые вы получите в будущем).
Если это значение NPV больше, чем первоначальные инвестиции (которые составляли 50 000 долларов США), вы получите прибыль, а если нет, то у вас будут убытки.
NPV широко используется при оценке капитальных проектов и принятии инвестиционных решений.
Это может помочь вам узнать, являются ли ваши инвестиции или проект прибыльными или нет.
В Excel его можно рассчитать с помощью функции NPV. Это довольно просто и делает расчет NPV очень простым.
В этой статье вы узнаете об этой функции и предупредите об ограничениях и предварительных требованиях.
Функция Excel NPV
Функция NPV в Excel имеет следующие параметры:
=ЧПС(ставка, значения)
- ставка – учетная ставка за период
- значений – массив ячеек, содержащих будущие платежи (отрицательное значение) или доходы (положительное значение).
Вот некоторые важные предпосылки для использования функции:
- функция принимает в расчет только числовые значения, а все остальные игнорируются
- значения появляются в конце каждого периода
- значения находятся в хронологическом порядке (от самого старого) и имеют одинаковую пространственно-временную
- скидку ставка должна быть отформатирована в процентах
- все периоды должны иметь свое значение
Обратите внимание, что для этой функции необходимо иметь регулярный приток или отток значений.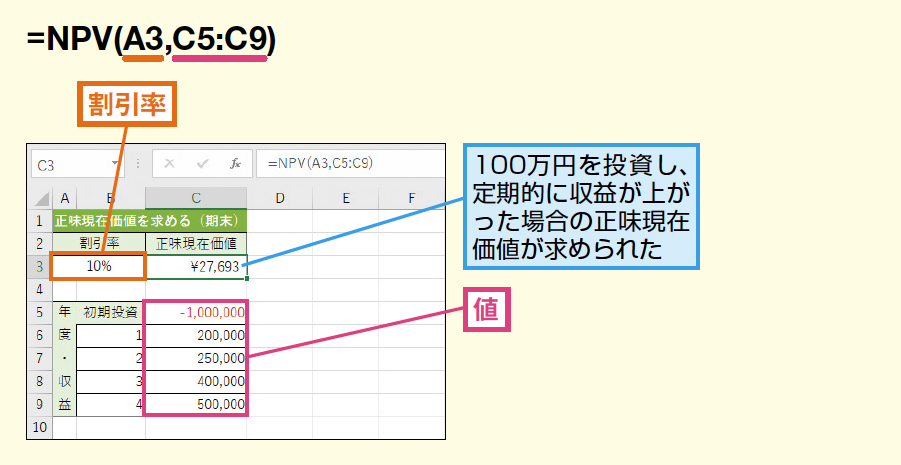 Если вы работаете с данными, в которых приток/отток происходит через нерегулярные промежутки времени, вам придется использовать функцию XNPV (описанную далее в этом руководстве).
Если вы работаете с данными, в которых приток/отток происходит через нерегулярные промежутки времени, вам придется использовать функцию XNPV (описанную далее в этом руководстве).
Расчет чистой приведенной стоимости (NPV) в Excel
Допустим, у вас есть следующие данные о движении денежных средств (в столбце C). У вас также есть ставка дисконтирования (в ячейке E2), и теперь вы хотите рассчитать чистую приведенную стоимость денежных потоков
.В столбце C у нас есть денежный поток, где первоначальные инвестиции в конце периода 1 (C2) являются отрицательными (-20 000 долларов США).
В ячейках C3:C8 у нас есть будущие доходы от инвестиций, которые положительны. Ставка дисконтирования 5,50% указана в ячейке E2.
На основе этих входных данных вы хотите рассчитать чистую приведенную стоимость.
Приведенная ниже формула даст вам значение NPV для этих данных:
=ЧПС(Е2,С3:С8)+С2
Позвольте мне быстро объяснить, что здесь происходит.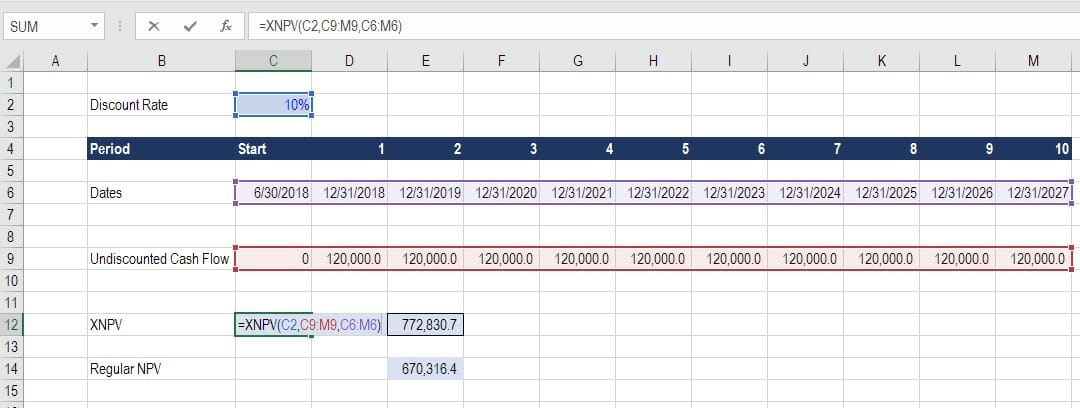
Мы использовали формулу NPV и проигнорировали значение в ячейке C2, так как это начальный отток.Это деньги, которые уйдут из кармана в первый день.
Но тогда у нас есть притоки, которые приходят в конце каждого периода. Таким образом, значение в ячейке C3 приходится на конец 1-го года, а значение в ячейке C4 — на конец 2-го года.
Таким образом, мы использовали формулу NPV для расчета чистой приведенной стоимости всех притоков, а затем добавили к формуле первоначальный отток в размере -$20 000.
Это дает нам окончательную чистую приведенную стоимость общих денежных потоков проекта.
Теперь, если это значение положительное, мы будем считать проект прибыльным, а если отрицательное, то будем считать его убыточным.
Обратите внимание, что мы игнорируем только исходный поток. Если в течение срока действия проекта будет больше оттоков, они будут использоваться в формуле NPV (но убедитесь, что оттоки имеют отрицательные значения).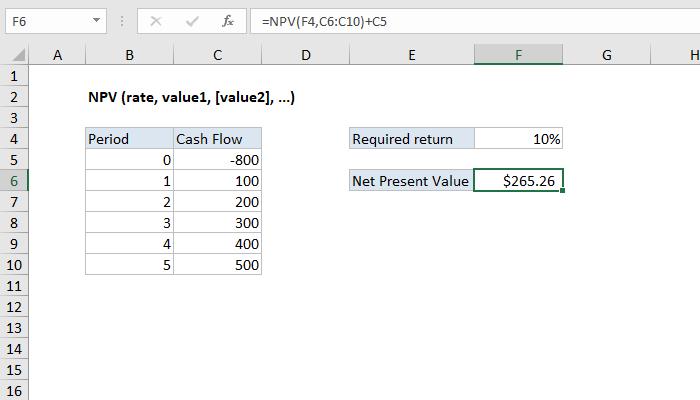
Использование функции NPV для сравнения нескольких проектов
Вы также можете использовать функцию NPV, чтобы сравнить инвестиции в несколько проектов и решить, какой проект является наиболее прибыльным.
Вам просто нужно указать ставку дисконтирования, первоначальные инвестиции для каждого проекта и денежные потоки.
Логика здесь проста – вы рассчитаете чистую приведенную стоимость всех проектов и выберете тот, у которого самая высокая чистая приведенная стоимость.
Допустим, у вас есть 3 проекта со своими инвестициями (C2, D2, E2) и денежными потоками (C3:C8, D3:D8, E3:E8).
В ячейке C10 указана ставка дисконтирования 5,50%, а в ячейках C11, D11 и E11 требуется получить чистую приведенную стоимость для всех трех проектов.
В ячейках C11, D11 и E11 формулы соответственно:
=ЧПС(10 канадских долларов,C3:C8)+C2
=ЧПС(10 канадских долларов,D3:D8)+D2
=ЧПС(10 канадских долларов,E3:E8)+E2
Как видите:
- Инвестиция 1 имеет чистую приведенную стоимость в размере 5 111 долларов США
- Инвестиция 2 имеет чистую приведенную стоимость в размере 2 946 долларов США
- Инвестиция 3 имеет чистую приведенную стоимость в размере 5 366 долларов США.

Теперь вы можете легко сравнить эти три проекта и сделать вывод, что третий проект является наиболее прибыльным.
Разница между функциями NPV и XNPV в Excel
Как вы уже узнали, для функции NPV в Excel требуются точно такие же периоды времени для денежного потока.
С другой стороны, функция XNPV позволяет вводить конкретные даты для каждого значения. Эти даты могут приходиться на нерегулярные периоды.
Если вы попытаетесь использовать обе функции для получения чистой приведенной стоимости денежного потока, происходящего в нерегулярные периоды, вы увидите большую разницу в результатах.Таким образом, функция XNPV намного точнее, чем NPV.
Ниже приведен синтаксис функции XNPV:
=XNPV(ставка, значения, даты)
- ставка – учетная ставка за период
- значения – массив ячеек, содержащих будущие платежи (отрицательное значение) или доходы (положительное значение)
- даты – даты, в которые происходит движение денежных средств
Допустим, что вы имеют следующий денежный поток и ставку дисконтирования и хотят рассчитать чистую приведенную стоимость, используя функции NPV и XNPV.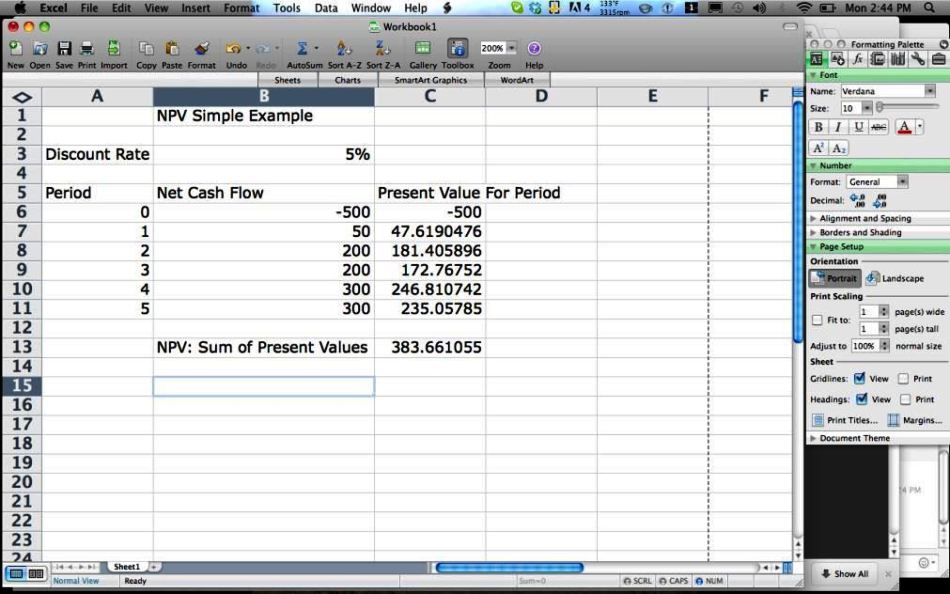
В столбце C представлен денежный поток, где первоначальные инвестиции в конце периода 1 (C2) являются отрицательными (-20 000 долларов США). В ячейках C3:C8 у вас есть будущие доходы от инвестиций, которые положительны.
Дата каждого дохода указана в ячейках D2:D8. Ставка дисконтирования 5,50% указана в ячейке F2.
На основе этих входных данных вы хотите рассчитать чистую текущую стоимость с помощью двух функций.
Формула в ячейке G2 предназначена для расчета чистой приведенной стоимости без учета дат:
=ЧПС(F2,C3:C8)+C2
Формула в ячейке h3 использует XNPV, где также учитываются даты:
=XNPV(F2,C2:C8,D2:D8)
Как видите, функция NPV вернула 27 156 долларов США в G2, а функция XNPV вернула 38 387 долларов США.
Причина этого различия заключается в том, что NPV считает, что каждый денежный поток происходит в конце периода, в то время как XNPV будет учитывать точную дату и соответствующим образом дисконтировать ее. В большинстве случаев ваше значение с XNPV будет выше или равно значению NPV.
В большинстве случаев ваше значение с XNPV будет выше или равно значению NPV.
Поэтому, если используются даты, используйте XNPV для расчета чистой приведенной стоимости в Excel.
Надеюсь, этот урок был вам полезен!
Другие учебники по Excel, которые вам также могут понравиться:
Расчет чистой приведенной стоимости (NPV) с помощью Excel
В прошлом, когда я преподавал концепцию NPV (чистой приведенной стоимости), я часто спрашивал, все ли ее понимают.Если нет, то я расскажу об этом в общих чертах. Некоторые учебные модули могут показаться сложной концепцией. Но на самом деле это намного проще, чем кажется на первый взгляд.
NPV — это функция в Excel, которая помогает вам рассчитать разницу между деньгами, которые вы получаете (притоки денежных средств), и деньгами, которые вы платите (оттоки денежных средств) за проект или инвестиции. Положительный результат функции будет означать прибыльный проект/инвестицию.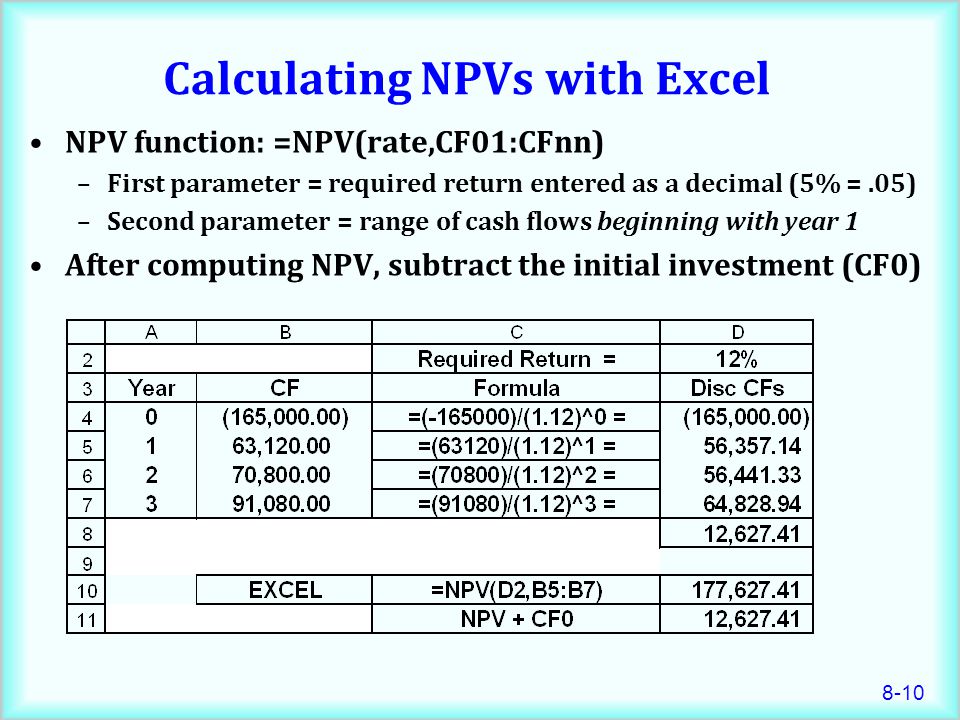 Отрицательный результат будет означать чистый убыток.
Отрицательный результат будет означать чистый убыток.
В Excel используется синтаксис функции NPV(ставка,значение1,[значение2],…).Укажите скорость и значение1. Значение 2 и т. д. не требуются, но вы можете иметь до 254 значений. Ставка — это ставка дисконтирования, инфляция или ставка конкурирующей инвестиции. Каждое значение в функции представляет отдельный платеж или доход по проекту/инвестиции. Если у вас уже есть платежи/доходы в ячейках Excel, вы можете использовать их в функции.
Я создал очень простой пример. Ставка составляет 6%, а суммы платежей/доходов указаны в Excel для первоначальных затрат, а затем для возврата в течение 4 лет.См. рис. 1.
Рисунок 1
Первоначальные затраты и доход за 4-й год отрицательны, поскольку представляют собой отток денежных средств. Доходность за годы 1-3 положительна, что указывает на приток денежных средств. Поскольку функция NPV основана на будущих денежных потоках, вы не можете включать первоначальные затраты в начале первого года/периода в аргументы функции. Вы добавляете его в конце. Если у вас есть значение первоначальных затрат в конце первого года, вы можете включить его в аргументы функции NPV.
Вы добавляете его в конце. Если у вас есть значение первоначальных затрат в конце первого года, вы можете включить его в аргументы функции NPV.
Формула для NPV будет =NPV(B3,B7:B10)+B6. Если у вас есть дополнительные суммы, вы можете использовать запятую для разделения разных ячеек или диапазонов ячеек. См. результаты на рисунке 2.
Рисунок 2
Определение чистой приведенной стоимости проекта или инвестиции может помочь в принятии решений относительно бюджета и вариантов проекта. Стоит потратить время на анализ, чтобы убедиться, что вы делаете лучший выбор для своей организации.
Изображение предоставлено: https://www.flickr.com/photos/pgasston/
Узнайте, как рассчитать чистую приведенную стоимость с квартальными денежными потоками в Excel
К настоящему времени должно быть легко рассчитать чистую приведенную стоимость в Excel с учетом годовых денежных потоков. Но что, если мы хотим рассчитать то же самое, но с ежеквартальными денежными потоками? В этом посте будет представлено пошаговое руководство по , как рассчитать чистую приведенную стоимость с квартальными денежными потоками в Excel .
Рисунок 1: Как найти чистую приведенную стоимость, если денежные потоки являются ежеквартальными
Общий синтаксис формулы =ЧПС (ставка, денежные потоки) + Первоначальные инвестиции
Где;
- Ставка — будет относиться к квартальной ставке.Возьмем годовую ставку, умножив ее на квартал .
- Денежные потоки — относится к количеству кварталов, которые у нас есть в указанном периоде. Возьмем периоды, умноженные на кварталы, .
Использование формулы NPV имеет основополагающее значение, когда дело доходит до определения NPV, даже если у нас есть ежеквартальные денежные потоки.
Все, что нам нужно знать, это понять, как сделать ставку и денежный поток квартальными, если они даны в годовом исчислении.
Как работает формула Чтобы рассчитать чистую текущую стоимость с заданными первоначальными инвестициями, годовыми денежными потоками и годовой ставкой, нам нужно сначала сделать ставку и время ежеквартально.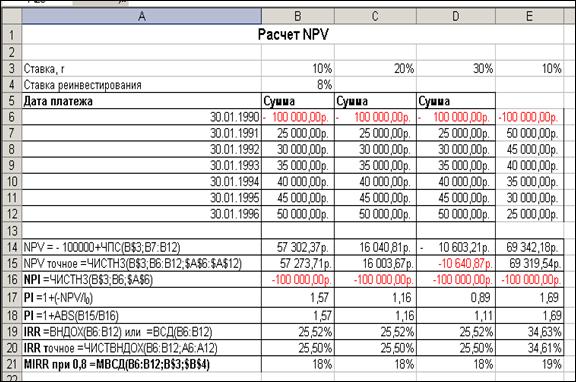
Для этого умножаем скорость на четверть и делим время на четверть.
Если у нас есть это, мы продолжаем находить NPV обычным способом, используя формулу;
=ЧПС (ставка, денежные потоки) + Первоначальные инвестиции
Предполагая, что у нас есть первоначальные инвестиции в размере 100 долларов США и денежные потоки в размере 80 долларов США в течение 2 лет, какова будет ЧДП при процентной ставке 10%?
Действуем следующим образом;
Шаг 1: Подготовьте и занесите таблицу Excel
Рисунок 2: Пример определения чистой приведенной стоимости по квартальным денежным потокам
Шаг 2: Подготовьте столбец для годовых и квартальных данных, как показано выше.
Шаг 3: Введите формулу с квартальными данными в ячейку, где вы хотите получить результат для чистой приведенной стоимости с квартальными денежными потоками.
Шаг 4 : Нажмите Enter, чтобы получить ответ.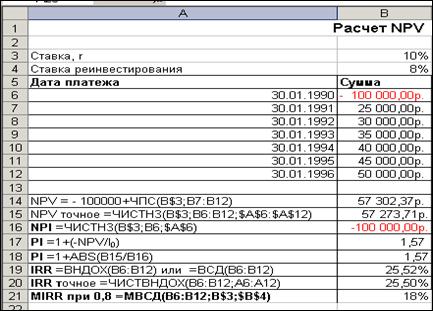
В большинстве случаев проблема, которую вам нужно будет решить, будет более сложной, чем простое применение формулы или функции. Если вы хотите сэкономить часы исследований и разочарований, попробуйте наш онлайн-сервис Excelchat! Наши эксперты по Excel доступны круглосуточно и без выходных, чтобы ответить на любой вопрос, который у вас может возникнуть.Мы гарантируем подключение в течение 30 секунд и индивидуальное решение в течение 20 минут.
NPV Calculator — Калькулятор внутренней нормы доходности и чистой приведенной стоимости для Excel
Компании используют расчет Net Present Value (NPV) , чтобы решить, добавят ли инвестиции ценность в долгосрочной перспективе, сравнить различные варианты инвестиций и решить, стоит ли внедрять новый продукт. В дополнение к объяснению того, как рассчитать NPV и IRR , вы можете скачать Free Excel NPV Calculator , чтобы помочь вам настроить свою собственную электронную таблицу финансового анализа.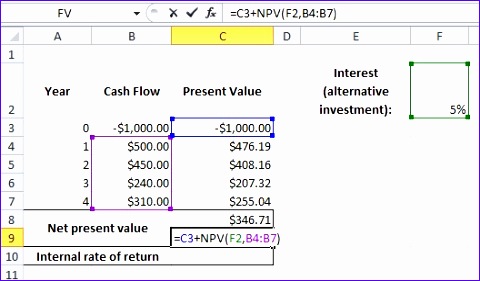
Реклама
В отличие от анализа безубыточности, который основан на чистой прибыли, равной 0, чистая приведенная стоимость включает ставку дисконтирования или ставку или доход, который можно получить, например, от альтернативных инвестиций на финансовом рынке. Если расчет NPV > 0 , то новая продуктовая линейка (или что-то еще, что вы анализируете) может иметь смысл.
Внутренняя норма прибыли или IRR — еще один полезный показатель для анализа инвестиций.Функция IRR в Excel использует тот же ряд денежных потоков, что и NPV, но она должна иметь по крайней мере одно отрицательное (обычно при t = 0) и одно положительное значение, и для нее требуется начальное предположение о ставке, поскольку расчет является итеративным. Электронная таблица NPV Calculator также включает расчет IRR.
Калькулятор NPVс IRR, XNPV и XIRR
для Excel, Google Sheets и OpenOfficeОписание
Рабочая книга содержит два рабочих листа:
1) Рабочий лист NPV Calculator , показанный на снимке экрана выше, позволяет рассчитать NPV и IRR для нескольких серий денежных потоков.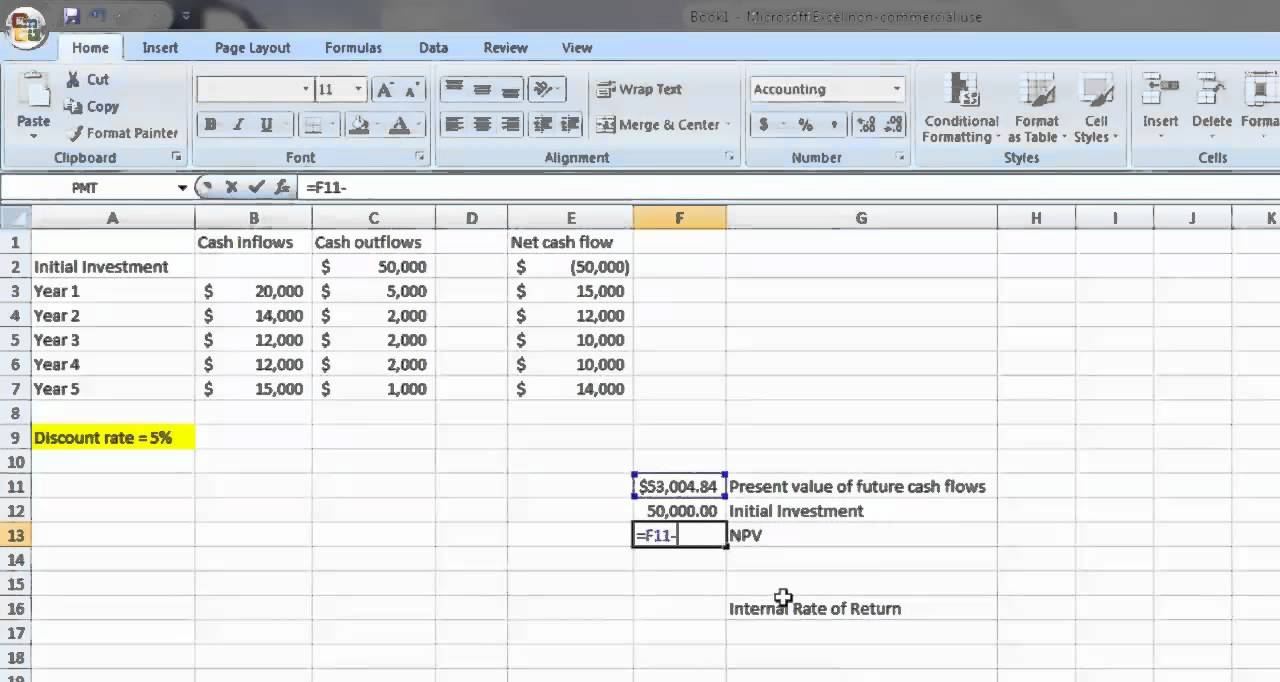
2) XIRR, XNPV Calculator на снимке экрана справа использует функции Excel XNPV и XIRR для расчета чистой приведенной стоимости и внутренней нормы доходности для непериодического ряда денежных потоков (на основе дат).
— добавьте свою собственную серию и/или автоматически сгенерируйте серию однородного, градиентного или экспоненциального градиента.
— Узнайте, как настроить денежные потоки и формулы NPV и IRR.
Как рассчитать IRR и NPV в Excel
Чтобы рассчитать NPV или IRR , сначала необходимо иметь прогнозируемый или оценочный ряд периодических денежных потоков .Обычно это включает в себя некоторый первоначальный единовременный платеж в качестве первоначальных инвестиций (отрицательный денежный поток) в момент времени t = 0, за которым следуют как притоки (доходы), так и оттоки (платежи) через равные промежутки времени t = 1, t = 2, t = 3, и т. д. На изображении ниже показан пример.
Рис. 1. Пример ряда денежных потоков
с расчетом NPV и IRR.
Рис. 2. Схема движения денежных средств.
Чистая приведенная стоимость определяется как « разница между текущей стоимостью (PV) будущих денежных потоков от инвестиций и суммой инвестиций » [1] (курсив наш).
Это отличное определение, потому что оно объясняет, почему формула чистой приведенной стоимости в Excel на самом деле неполная, и что вам нужно сделать, чтобы правильно ее использовать. Слово «чистый» в NPV подразумевает вычитание чего-то из чего-то другого. Функция Excel NPV на самом деле вычисляет только сумму текущей стоимости будущих денежных потоков . Обратите внимание на «будущее», что означает денежные потоки, начинающиеся в момент времени t=1 или 1 период в будущем с настоящего момента времени t=0.
Чтобы рассчитать NPV, вы также должны вычесть стоимость первоначальных инвестиций или, другими словами, добавить денежный поток в момент времени t=0 (что является отрицательным значением). Таким образом, на Рисунке 1 выше уравнение для NPV:
Таким образом, на Рисунке 1 выше уравнение для NPV:
=ЧПС(ставка, значения_t1_to_tn) + значение_t0 =ЧПС(B1,B5:B8)+B4
Формула внутренней нормы доходности (IRR) на рисунке 1:
=IRR(values_t0_to_tn, предположение) =ВНР(B4:B8,0.1)
Было бы неплохо прочитать справку по функциям NPV и IRR, чтобы понять некоторые ограничения и требования.
Полезно отметить, что формула NPV идентична расчету текущей стоимости всех будущих денежных потоков с использованием формулы PV и их суммировании, как показано на рисунке 1.Это также можно сделать с помощью формулы массива, как объяснено Тимоти Майерсом в ссылке [2] ниже. Формула массива на самом деле более мощная, чем функция NPV, потому что вы можете включить начальный денежный поток в момент t = 0, чтобы не добавлять его отдельно, и вы можете иметь несколько значений для одного и того же периода или даже периоды вне приказ.
=СУММ(PV(скорость, периоды_t0_to_tn, 0, -значения))
Использование формул XNPV и XIRR для расчета NPV и IRR
Второй рабочий лист в электронной таблице NPV Calculator создан, чтобы помочь вам рассчитать чистую текущую стоимость и внутреннюю норму прибыли для серии запланированных денежных потоков, которые не являются периодическими.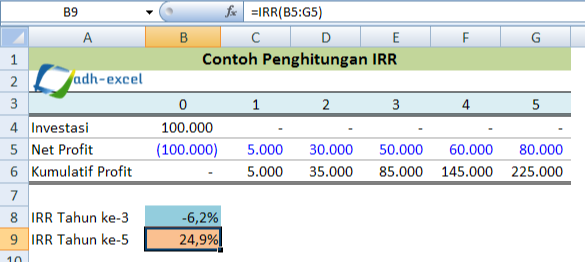 Функции XNPV и XIRR требуют ввода дат в дополнение к значениям денежного потока и ставке дисконтирования . Они используют 365-дневный год для расчета приведенной стоимости на основе первоначального отрицательного значения (инвестиции).
Функции XNPV и XIRR требуют ввода дат в дополнение к значениям денежного потока и ставке дисконтирования . Они используют 365-дневный год для расчета приведенной стоимости на основе первоначального отрицательного значения (инвестиции).
XIRR относится к XNPV, как IRR относится к NPV
Следующая формула массива может использоваться вместо формулы XNPV, если вам нужно использовать 360-дневный год или вы не хотите использовать пакет инструментов анализа.((даты-ИНДЕКС(даты,1))/365)))
Ссылки
- [1] Определение чистой приведенной стоимости по адресу http://www.businessdictionary.com/definition/net-present-value-NPV.html
- [2] Функция NPV не вычисляет чистую текущую стоимость Тимоти Р. Мэйс, функция NPV.
- Учебное пособие по функции значения времени Тимоти Р.Мэйс, http://www.tvmcalcs.com/calculators/excel_tvm_functions/excel_tvm_functions_page3
Как цитировать эту страницу
Чтобы порекомендовать калькулятор NPV или процитировать эту страницу со своего веб-сайта или блога, используйте ссылку, подобную приведенной ниже.
— Виттвер, Дж. В., «Как рассчитать NPV и IRR в Excel», с сайта Vertex42.com.
Заявление об отказе от ответственности : Эта таблица калькулятора чистой приведенной стоимости и информация на этой странице предназначены только для иллюстративных и образовательных целей.Мы не гарантируем результаты или применимость к вашей уникальной финансовой ситуации. Вам следует обратиться за советом к квалифицированным специалистам относительно финансовых решений.
Как рассчитать NPV в Excel?
В этой статье вы узнаете, как рассчитать NPV (чистую текущую стоимость) с помощью Excel. Функция Excel для расчета NPV — «NPV».
NPV, или чистая текущая стоимость, представляет собой текущую или фактическую стоимость будущих денежных потоков. Текущая стоимость будущего денежного потока – это его текущая стоимость.Чтобы узнать текущую стоимость, вы должны использовать ставку дисконтирования. NPV включает не только положительные денежные потоки или притоки, но и все расходы, включая первоначальные инвестиции.
Если чистая приведенная стоимость положительна, это означает, что фактическая стоимость всех доходов выше, чем фактическая стоимость всех расходов, и инвестиции желательны, поскольку они добавляют больше ценности, чем наилучшая альтернатива.
Денежные потоки дисконтируются с использованием ставки дисконтирования, соответствующей наилучшей альтернативной инвестиции.
ШАГ 1. Знайте свой денежный поток
Первым шагом для расчета чистой приведенной стоимости с помощью Excel является ввод всех денежных потоков инвестиционного проекта. Обычно потоки рассчитываются за год, но можно использовать и месяцы. Учтите, что период ставки дисконтирования должен соответствовать периоду движения денежных средств. Например, если вы используете годовые денежные потоки, ставка дисконтирования должна быть годовой.
Денежные потоки обычно оцениваются с помощью модели.
ШАГ 2. Узнайте свою ставку скидки
Выберите ячейку и введите ставку скидки. Например, если ваша ставка дисконтирования составляет 10 %, введите 0,1
Например, если ваша ставка дисконтирования составляет 10 %, введите 0,1
. Помните, что ставка дисконтирования – это норма прибыли для ваших лучших альтернативных инвестиций с риском, аналогичным текущему проекту.
ШАГ 3. Введите формулу NPV Excel
Формула NPV требует 2 аргумента:
пример.
Учтите, что формула Excel NPV начинается с первого периода, а первоначальные инвестиции происходят в период «0».Итак, мы должны вычесть первоначальные инвестиции из предыдущего расчета. Примечание: некоторые сайты ошибаются, они включают первоначальные инвестиции в формулу NPV. Это приводит к незначительной разнице, поскольку Excel предполагает, что первый период составляет один год вперед.
Формула Excel:
=ЧПС(E3,B5:B14)+B4
Где:
E3: ячейка, содержащая ставку дисконтирования.
B5:B14: диапазон, содержащий будущие денежные потоки
B4: ячейка, содержащая первоначальные инвестиции (в этом примере первоначальные инвестиции выражены в отрицательных значениях, поэтому мы добавляем их)
Нажмите Enter, и Excel рассчитает NPV .
Формула NPV Excel — Расчет чистой приведенной стоимости
В этом учебном пособии показано, как использовать функцию Excel NPV в Excel для расчета чистой приведенной стоимости ряда денежных потоков.
NPV Описание функции:
Функция NPV Вычисляет чистую текущую стоимость.
Чтобы использовать функцию рабочего листа Excel NPV, выберите ячейку и введите:
(Обратите внимание на то, как появляются поля ввода формулы)
Синтаксис функции NPV и входные данные:
=ЧПС(ставка,значение1,[значение2],…) |
ставка — это процентная ставка или дисконтированная ставка за один период. Его следует вводить в виде процентного значения или десятичного числа.
value1 — это числовые значения, которые представляют серию регулярных денежных потоков.
value2 – НЕОБЯЗАТЕЛЬНО: второе значение(я), представляющее денежные потоки.
Разница между приведенной стоимостью притока и оттока денежных средств за определенный период представляет собой чистую приведенную стоимость (NPV).Предполагается, что для того, чтобы инвестиции были прибыльными, их чистая приведенная стоимость должна быть положительной, а если чистая приведенная стоимость отрицательна, то инвестиции приведут к чистым убыткам.
Просто рассчитывается как:
Что такое функция Excel NPV?Функция Excel NPV вычисляет чистую текущую стоимость инвестиции на основе ее дисконтированной ставки или процентной ставки и ряда будущих денежных потоков. Функция Excel NPV использует следующее уравнение для расчета чистой приведенной стоимости инвестиций:
Где:
n = количество периодов времени
i = номер периода
Ставка= ставка дисконтирования или процентная ставка
значений = денежный поток
Расчет Чистая текущая стоимость бизнеса Предположим, мы начинаем бизнес, и в конце первого года потребуются первоначальные инвестиции в размере 100 000 долларов США.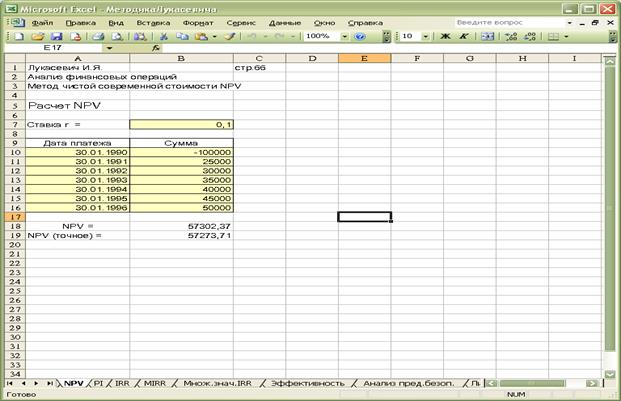 И ожидается, что бизнес начнет приносить прибыль со второго года. Прибыль за второй, третий, четвертый и пятый год прогнозируется на уровне 20 000, 35 000, 50 000 и 80 000 долларов соответственно. Норма прибыли, которую мы могли бы получить при альтернативных инвестициях, составляет 10%. Итак, нам нужно узнать чистую текущую стоимость бизнеса.
И ожидается, что бизнес начнет приносить прибыль со второго года. Прибыль за второй, третий, четвертый и пятый год прогнозируется на уровне 20 000, 35 000, 50 000 и 80 000 долларов соответственно. Норма прибыли, которую мы могли бы получить при альтернативных инвестициях, составляет 10%. Итак, нам нужно узнать чистую текущую стоимость бизнеса.
Первоначальные инвестиции в бизнес вводятся с отрицательным знаком, поскольку они представляют собой исходящие денежные средства
Значение 1 = -100 000 долларов США
Формула, используемая для расчета чистой приведенной стоимости бизнеса:
Чистая приведенная стоимость бизнеса, рассчитанная с помощью функции Excel NPV, равна
.NPV = 24 226 долларов США.66.
Расчет чистой приведенной стоимости проекта Рассчитаем чистую приведенную стоимость проекта, в который в начале были вложены инвестиции в размере 10 000 долларов. Годовая учетная ставка составляет 8%. Доходы с 1-го -го года по 4-й -й -й год приведены в таблице выше.
Годовая учетная ставка составляет 8%. Доходы с 1-го -го года по 4-й -й -й год приведены в таблице выше.
Формула, используемая для расчета:
Чистая приведенная стоимость бизнеса, рассчитанная с помощью функции Excel NPV, равна
.NPV = 9 437 долларов США.1
После вычета первоначальных инвестиций из приведенного выше значения мы получим более полное представление об инвестициях
NPV (после вычета первоначальных инвестиций) = 9 437,1 долл. США – 10 000 долл. США = -562,90 долл. США
Чистая текущая стоимость бизнеса составляет -$562,90.
Результат NPV получился отрицательным, это означает, что инвестиции по-прежнему не будут прибыльными в конце 4 -го -го года.
NPV
в Google ТаблицахВсе приведенные выше примеры работают точно так же в Google Таблицах, как и в Excel.
Дополнительные примечания
Используйте функцию NPV для расчета чистой приведенной стоимости инвестиции.
Значения должны быть в хронологическом порядке. Таким образом, значения платежа и дохода должны быть введены в правильной последовательности, и эти значения должны приходиться на конец периода.
В Excel 2007–2019 можно ввести от 1 до 254 аргументов значений, которые представляют платежи и доходы. В Excel 2003 и более ранних версиях можно ввести до 30 аргументов-значений.
Притоки денежных средств (при получении денежных средств, таких как купонные выплаты) имеют положительный знак, а оттоки денежных средств (когда выплачиваются денежные средства, например, деньги, используемые для покупки инвестиций) имеют отрицательный знак.
Функции NPV и PV (текущая стоимость) очень похожи. Единственная разница между NPV и PV заключается в том, что PV позволяет денежным потокам начинаться в начале инвестиционного периода, а также в конце инвестиционного периода.
Требуются периодические денежные потоки. Денежные потоки чаще всего происходят на постоянной основе каждый период.

 При данной ставке инвестор вернет вложенные первоначально средства. Инвестиции состоят из платежей (суммы со знаком «–») и доходов (со знаком «+»), которые происходят в одинаковые по продолжительности временные промежутки.
При данной ставке инвестор вернет вложенные первоначально средства. Инвестиции состоят из платежей (суммы со знаком «–») и доходов (со знаком «+»), которые происходят в одинаковые по продолжительности временные промежутки. Формула производит циклические вычисления с того значения, которое указано в аргументе «Предположение». Если аргумент опущен, со значения 0,1 (10%).
Формула производит циклические вычисления с того значения, которое указано в аргументе «Предположение». Если аргумент опущен, со значения 0,1 (10%).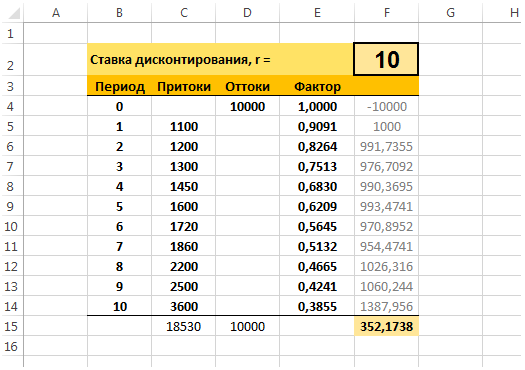
 Графический метод показал результат ВСД, аналогичный найденному в Excel.
Графический метод показал результат ВСД, аналогичный найденному в Excel. По крайней мере, один из денежных потоков должен быть положительным, и, по крайней мере, один должен быть отрицательным.
По крайней мере, один из денежных потоков должен быть положительным, и, по крайней мере, один должен быть отрицательным.
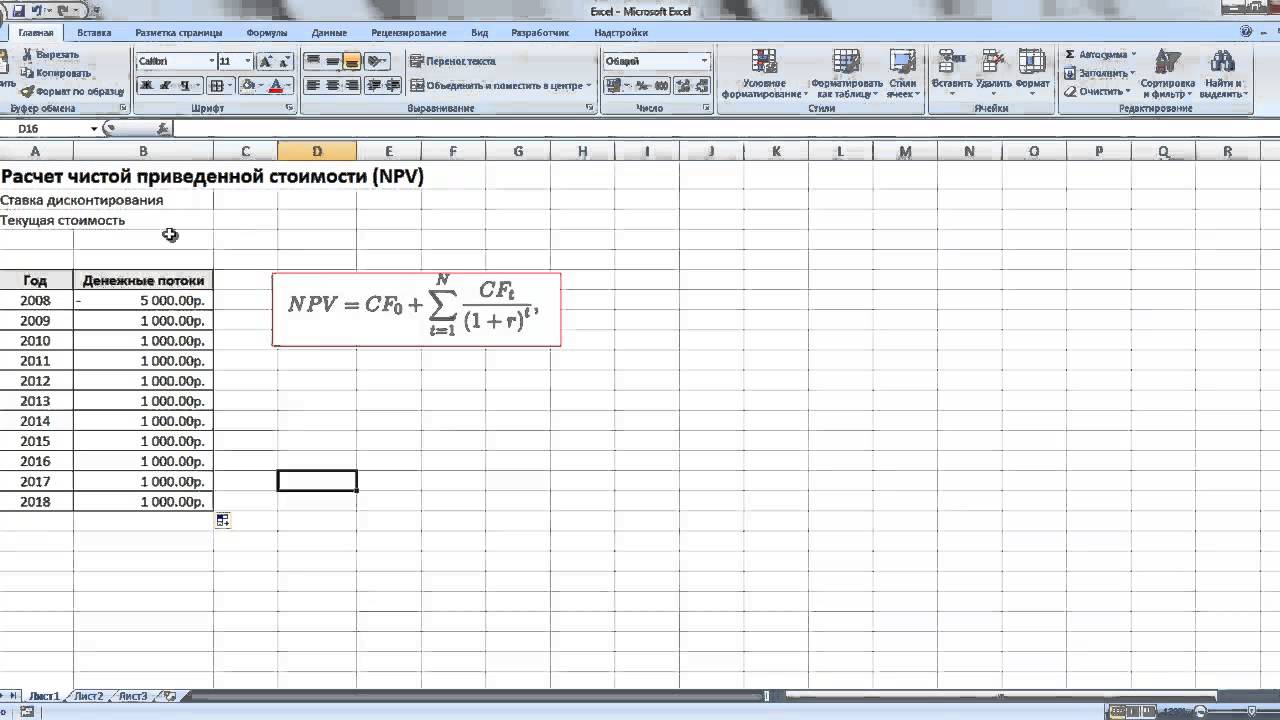

 Затем, чем выше IRR, тем лучше, поскольку он представляет процентную ставку, которую получает инвестор.
Затем, чем выше IRR, тем лучше, поскольку он представляет процентную ставку, которую получает инвестор.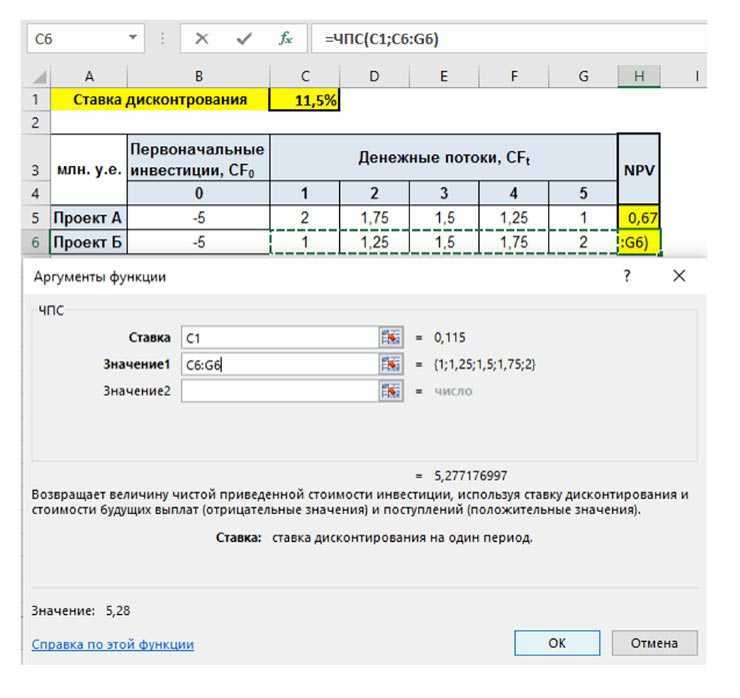
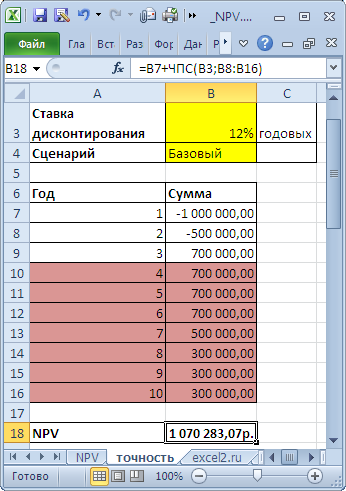 ..)
..)