VAR — техническая схема расчета
Одним из основных этапов оценки риска является подготовка данных — итоговая оценка риска во многом зависит от того, какой показатель и за какой период используется для расчета, причем для нестабильных развивающихся рынков вклад этого фактора в формирование конечной оценки риска становится первостепенным.
Здесь, в рамках общего подхода к статистическому анализу стоимости позиции, возможны два варианта:
1. Анализ текущей стоимости позиции.
2. Анализ динамики доходов и расходов.
Технически указанные варианты практически аналогичны, и выбор между ними должен осуществляться исходя из специфики объекта анализа. В рамках данной статьи, ориентированной на специфику российского рынка, за основу будет принят первый вариант.
Анализ текущий стоимости позиции, превалирующий в теоретической литературе и широко распространенный на практике, более универсален в реализации: для оценки риска необходима лишь регулярная (обычно – ежедневная) информация о рыночной стоимости текущей позиции.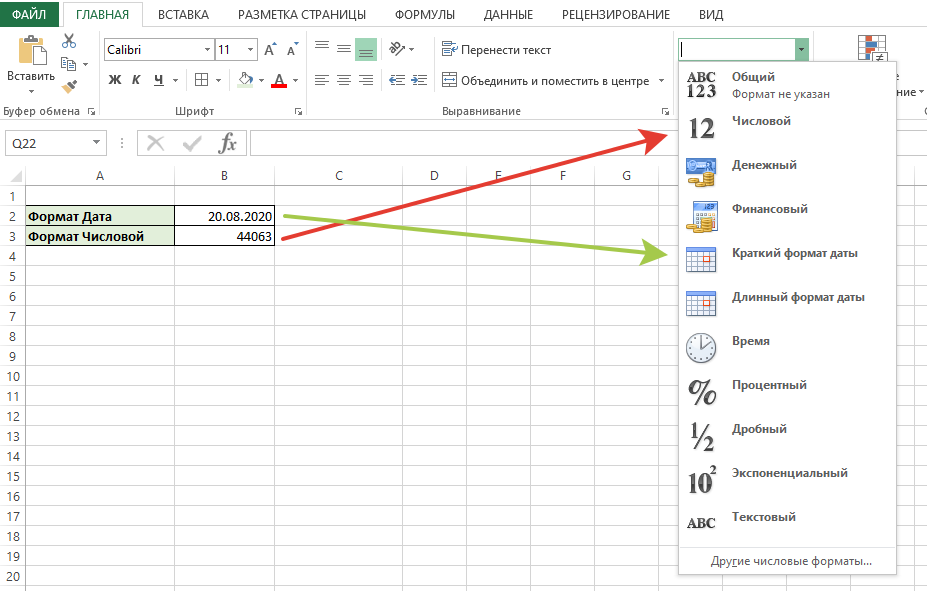
Анализ доходов и расходов требует данных о результатах торговых операций за аналогичное количество торговых дней, причем для статистической корректности оценок каждый торговый день должен складываться из десятков и сотен сделок. Такой анализ возможен лишь для крупнейших операторов рынка, однако его несомненным преимуществом является принятие во внимание, помимо рыночных факторов, индивидуальной торговой стратегии. В этой связи последние годы именно этот вариант оценки VAR получает широкое распространение среди лидеров мирового финансового рынка.
При этом, в контексте агрегирования оценок отдельных рисков в общую оценку совокупного риска, разница между рассматриваемыми подходами достаточно существенна.
Итак, на первом этапе подготовки данных определяется исходный ряд показателей – ряд значений стоимости рассматриваемой (фиксированной) позиции для всех зафиксированных в историческом периоде состояний рынка. В зависимости от рыночных характеристик инструментов, составляющих позицию, специфики осуществляемых операций и целей анализа это может быть как непосредственно рыночная стоимость позиции, так и ее доходность, расчетные показатели цены (например, для опционов), а также ряд близких по экономическому смыслу рыночных показателей (сводных индексов и пр.
Полученный временной ряд переводится в ряд относительных изменений: (см. Пример 1 в формате MSExcel).
Рассмотрение дневных изменений является теоретически классическим и наиболее распространенным вариантом, однако, в ряде практических приложений встречаются варианты внутридневного анализа (с шагом по сделкам, или по установленным промежуткам времени) или шага изменений в несколько дней.
Практически в любом случае возникают проблемы с потерей значимых промежуточных рыночных событий, либо, при использовании перекрывающихся интервалов, — технические сложности с повторным учетом отдельных изменений (поскольку фактически, как это показано на Рисунке 1, каждый сдвиг уровня показателей ряда участвует в формировании нескольких изменений), однако, с другой стороны, возникает дополнительный эффект учета последовательности изменений.
На основе указанных данных осуществляется непосредственно оценка VAR.
Основными, классическими и в равной степени актуальными на современном этапе методами оценки VAR считаются:
- метод исторического моделирования;
- метод параметрической оценки, наиболее распространенный в форме вариационно-ковариационной модели;
- метод имитационного моделирования, часто именуемый по основной применяемой в его рамках модели методом Монте-Карло.

Историческое моделирование
Оценка VAR методом исторического моделирования является технически предельно простой и одновременно достаточно наглядной. Вместе с тем предлагаемый подход полностью укладывается в описанную выше концепцию моделирования.
Оценка VAR методом исторического моделирования в классическом варианте осуществляется по следующей схеме.
Полученный выше ряд относительных изменений упорядочивается, и очищается на часть наихудших значений, превышающую принятый доверительный уровень. Наихудшее из оставленных значений соответствует максимальной вероятной в рамках принятого доверительного уровня величине потерь, т.
 е. VAR – в соответствии с порядком расчета в форме относительного изменения стоимости (см. Пример 2 в формате MSExcel).
е. VAR – в соответствии с порядком расчета в форме относительного изменения стоимости (см. Пример 2 в формате MSExcel).Необходимо отметить, что в стандартном и наиболее распространенном варианте отсекаются наименьшие изменения, что, строго говоря, корректно исключительно:
- либо для анализа длинных позиций, для которых риск проявляется только в снижении рыночной цены;
- либо для рынков с симметричным распределением изменений в обоих направлениях (по отношению к среднему значению).
Как видно из приведенного выше примера, на практике распределения вероятностей не всегда являются строго симметричными. Более того, для рынков с ярко выраженными долгосрочными трендами роль фактора асимметрии часто возрастает.
Полученная относительная оценка VAR приводится к абсолютному денежному эквиваленту в соответствии с использованными показателями.
Вариационно-ковариационная модель
Вариационно-ковариационная модель представляет собой альтернативный параметрический подход к оценке VAR.
В основе модели лежит предположение о соответствии фактического распределения случайной величины (рыночного показателя) определенной теоретической закономерности. Соответственно, на рассматриваемый рыночный показатель проектируются выводы, сделанные на основании расчетов по теоретическому распределению.
Методологически данный способ оценки VAR требует определенного математико-статистического аппарата, не в полной мере прозрачного для пользователей, которые могут не иметь специализированного образования. Вместе с тем, с технической точки зрения расчет является в высшей степени простым и обеспечивает оперативный пересчет показателей при минимальном компьютерном интерфейсе (система может быть в полном объеме реализована на основе стандартных электронных таблиц).
Наиболее распространенным моделирования вариантом является приближение рассматриваемой случайной величины нормальным распределением.
 ч. в экономике. Для широкого круга сложных процессов, формируемых взаимодействием большого количества случайных факторов, анализ на основе закономерностей, теоретически выведенных для нормального распределения, является статистически корректным. Это характерно, в частности, и для многих финансовых показателей, а именно цен финансовых инструментов, валютных курсов, котировок ценных бумаг и т.п. (см., например, Рисунок 2). Высокая степень соответствия стандартного, детально изученного математической статистикой нормального распределения и фиксируемых на практике распределений изменений котировок финансовых инструментов позволяет распространить теоретически обоснованные в отношении нормального распределения зависимости на динамику котировок и получить оценку оценка стоимости, подверженной риску — VAR — вариационно-ковариационным методом.
ч. в экономике. Для широкого круга сложных процессов, формируемых взаимодействием большого количества случайных факторов, анализ на основе закономерностей, теоретически выведенных для нормального распределения, является статистически корректным. Это характерно, в частности, и для многих финансовых показателей, а именно цен финансовых инструментов, валютных курсов, котировок ценных бумаг и т.п. (см., например, Рисунок 2). Высокая степень соответствия стандартного, детально изученного математической статистикой нормального распределения и фиксируемых на практике распределений изменений котировок финансовых инструментов позволяет распространить теоретически обоснованные в отношении нормального распределения зависимости на динамику котировок и получить оценку оценка стоимости, подверженной риску — VAR — вариационно-ковариационным методом.Общая схема оценки VAR вариационно-ковариационным методом может быть представлена следующим образом.
На первом этапе определяются параметры нормального распределения, наилучшим образом приближающего фактическое распределение рассматриваемого показателя — полученного выше ряда относительных изменений. Технически это может быть сделано различными способами, среди которых простейшими для применения могут быть признаны реализованные в рамках стандартного интерфейса электронных таблиц функции подбора параметров распределения.
Технически это может быть сделано различными способами, среди которых простейшими для применения могут быть признаны реализованные в рамках стандартного интерфейса электронных таблиц функции подбора параметров распределения.
Далее необходимо определить значения обратного нормального распределения в соответствии с полученными ранее параметрами и:
- установленным доверительным уровнем – для короткой позиции, риск по которой оценивается по положительным изменениям, либо
- обратным доверительным уровнем (т.е. 1 – доверительный уровень) – для длинной позиции и, соответственно, отрицательных изменений (см. Пример 3 в формате MSExcel).
При этом практически указанные варианты идентичны. В рамках рассматриваемого метода, в соответствии с техническими ограничениями применяемого статистического инструментария, не предусмотрена асимметрия распределений – расхождение между положительными и отрицательными изменениями составит удвоенное среднее значение распределения (т. е. будет соответствовать статистически выделяемому линейному тренду). Таким образом, при построении модели предполагается, что в рамках сложившейся долгосрочной рыночной конъюнктуры разнонаправленные движения при одинаковом отклонении от математического ожидания равновероятны. Для инструментов, в отношении которых такое предположение не соответствует фактической динамике, применение вариационно-ковариационных оценок в чистом виде (без дополнительных корректировок) не корректно.
е. будет соответствовать статистически выделяемому линейному тренду). Таким образом, при построении модели предполагается, что в рамках сложившейся долгосрочной рыночной конъюнктуры разнонаправленные движения при одинаковом отклонении от математического ожидания равновероятны. Для инструментов, в отношении которых такое предположение не соответствует фактической динамике, применение вариационно-ковариационных оценок в чистом виде (без дополнительных корректировок) не корректно.
Описанная процедура относится к стандартному инструментарию математической статистики. По сути, это соответствует принятию рассчитанного исходя из общих свойств нормально распределенных случайных величин соотношения стандартного отклонения, математического ожидания и наихудшего значения, получаемого с установленной вероятностью.
Полученное значение — относительная оценка VAR — приводится к абсолютному денежному эквиваленту в соответствии с формой исходного статистического ряда.
Необходимо отметить, что представленный выше алгоритм соответствует оценке VAR для 1 инструмента. Для составных портфелей расчет осуществляется по аналогичной схеме, но с использованием несколько более сложного матричного математико-статистического аппарата, детализированное рассмотрение которого не представляется целесообразным в рамках данной статьи. Кроме того, технический учет исторических корреляций означает, с точки зрения экономического содержания модели, предположение о сохранении имевших место разнонаправленных движений инструментов, что в ряде случаев может привести к занижению оценки риска.
Для составных портфелей расчет осуществляется по аналогичной схеме, но с использованием несколько более сложного матричного математико-статистического аппарата, детализированное рассмотрение которого не представляется целесообразным в рамках данной статьи. Кроме того, технический учет исторических корреляций означает, с точки зрения экономического содержания модели, предположение о сохранении имевших место разнонаправленных движений инструментов, что в ряде случаев может привести к занижению оценки риска.
Вместе с тем, для простых портфелей с несущественной внутренней корреляцией в качестве объекта рассмотрения может быть принят синтетический (искусственно составленный) инструмент.
Имитационное моделирование
В рамках развития моделей оценки VAR качественно новым шагом стало применение имитационного моделирования по методу Монте-Карло, в соответствии с наименованием которого обычно именуется данная оценка VAR. Принципиальное отличие VAR Монте-Карло от оценок исторического и вариационно-ковариационного моделирования является та особенность, что объектом моделирования выступает не только величина потерь, но и стоимость самого инструмента. В рамках данного метода потери определяются не по отношению к текущей стоимости инструмента, но по отношению к ее будущему наиболее вероятному значению, что с формальной точки зрения существенно более корректно.
В рамках данного метода потери определяются не по отношению к текущей стоимости инструмента, но по отношению к ее будущему наиболее вероятному значению, что с формальной точки зрения существенно более корректно.
Имитационное моделирование достаточно мало формализовано и не имеет жестких формальных ограничений. В основу модели может быть положено любое, в т.ч. комбинированное, распределение случайных величин или другая функциональная зависимость. Указанная специфика, наряду с пошаговым характером моделирования, определяет гибкость и достаточно высокую универсальность данного метода. VAR Монте-Карло может быть рассчитан по портфелям любой сложности, содержащим как простые «прямые» инструменты, так и сложные производные, с определенными и опциональными платежами (т.е. предполагающие различные варианты реализации прав по инструменту). В рамках данного метода непосредственно моделирование VAR также может быть дополнено динамическими сценариями изменения риск-факторов и базовых портфелей.
В классическом варианте оценка VAR методом имитационного моделирования осуществляется следующим образом.
Исходным шагом является определение формы и параметров распределения (функциональной зависимости) для рассматриваемого ряда. Как было отмечено выше, в соответствии с широким распространением на финансовых рынках нормальным распределением случайных величин, в моделировании финансовых рисков доминирует аппроксимация изменений показателей на основе нормальных распределений. Вместе с тем технически инструментарий данной модели не содержит никаких ограничений в части вида распределения, допуская любые, в т.ч. комбинированные функции.
Далее осуществляется непосредственно моделирование ряда изменений, распределенного в соответствии с полученными параметрами (для чего при простых вариантах распределений может быть применен стандартный математико-статистический инструментарий).
В зависимости от конкретного подхода возможно моделирование:
- фиксированного количества точек (обычно, не менее 300), либо
- до стабилизации среднего значения результатов моделирования с установленной точностью (но не менее установленного количества точек).

По результатам моделирования определяется: - среднее ожидаемое изменение;
- наихудшее в рамках установленного доверительного уровня ожидаемое изменение по направлению, соответствующему анализируемой позиции;
- VAR-оценку риска как абсолютное значение разности указанных величин.
Вариант расчета для нормального распределения в формате MS Excel см. в Примере 4.
При этом моделирование может осуществляться как для отдельного инструмента, так и совместно для всех элементов портфеля. Моделирование также возможно как на 1 день, так и на более длительный (либо короткий) промежуток времени, в соответствии со специфическими целями анализа. В процесс моделирования могут также быть интегрированы сценарные элементы для учета опциональных инструментов, динамики портфелей и/или внешних рыночных факторов.
Необходимо отметить, что имитационное моделирование не дает однозначного результата – по итогам каждого расчета формируется индивидуальное значение.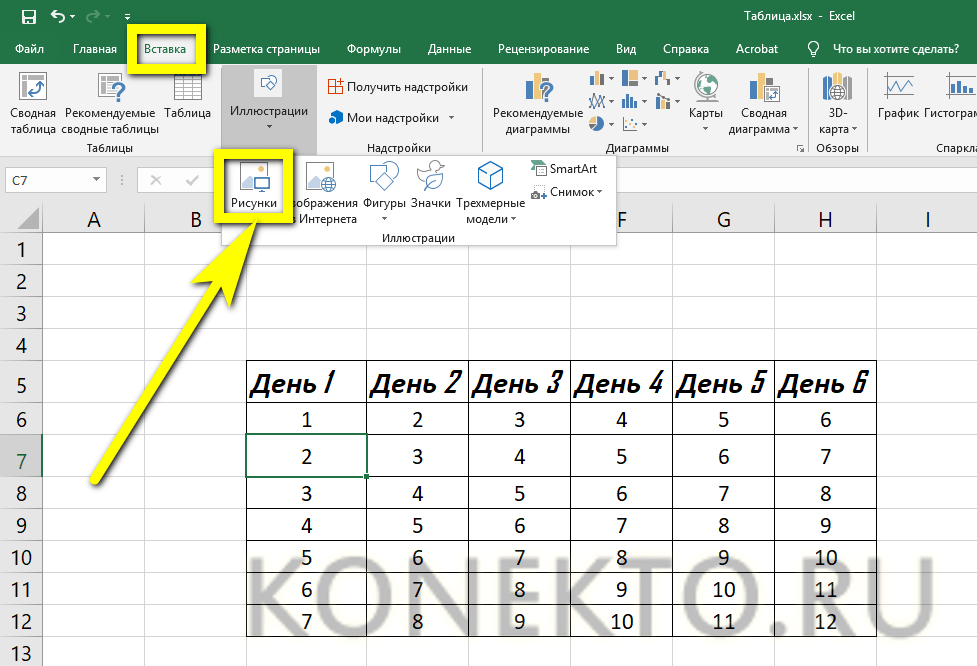 Естественно, при условии корректного построения модели разброс указанных значений ограничен. В зависимости от целей анализа могут варьироваться требования к точности расчета, однако для технической реализации высокоточной модели может потребоваться технически сложный инструментарий.
Естественно, при условии корректного построения модели разброс указанных значений ограничен. В зависимости от целей анализа могут варьироваться требования к точности расчета, однако для технической реализации высокоточной модели может потребоваться технически сложный инструментарий.
Несмотря на определенную случайную составляющую результатов имитационного моделирования, в целом, при условии корректности расчета, они соответствуют оценкам, получаемым с помощью других методов, с возможными отклонениями, определяемыми свойствами конкретных моделей.
| Комментарий к результатам моделирования по 3 рассмотренным методам |
| Результаты расчета VAR на примере фондового индекса РТС с использованием методов исторического, параметрического и имитационного моделирования приведены в Примере 5. При условии корректности построения моделей значения, полученные различными методами, в целом должны быть согласованы (как это видно из приведенного примера), однако они не должны в точности совпадать. 
Вместе с тем необходимо отметить следующие моменты, частично упоминавшиеся выше по тексту:
|
Модель хеджирования валютных рисков в Excel
Хитрости » 12 Август 2018 Дмитрий 6342 просмотровВ последнее время курс валют постоянно изменяется и предусмотреть то или иное изменение не так просто, что может обернуться серьезными потерями для компаний, доходы или расходы которых ведутся в иностранной валюте. Чтобы избежать подобных потерь финансовый директор предприятия может заранее сделать оценку рисков и составить программу хеджирования для наиболее существенных из них. Оценить размер рисков, основанных на курсах валют можно с помощью несложной модели в Excel.
Чтобы избежать подобных потерь финансовый директор предприятия может заранее сделать оценку рисков и составить программу хеджирования для наиболее существенных из них. Оценить размер рисков, основанных на курсах валют можно с помощью несложной модели в Excel.
Что такое хеджирование и когда его нужно применять?
Хеджирование – если простыми словами, то это перенос риска компании на другого участника рынка, используя финансовый актив.
Например, наша компания занимается продажей инструмента. В течение месяца мы ожидаем поставку партии товаров из Европы на сумму 100 000 евро. У компании на счете есть доллары, которые необходимо будет конвертировать в евро. Просчитав затраты и будущую прибыль, текущий курс евро к доллару нас устраивает. Но вот покупать евро на всю сумму контракта прямо сейчас, «заморозив» свои средства, ответственный менеджер не хочет. Он решает использовать хеджирование через заключение сделок на валютном рынке, но без реальной поставки средств. Т.е. он переводит часть средств на свой депозитный счет и открывает длинную позицию по паре евро/доллар (покупает евро, продает доллары) на сумму 100 000 евро. Сумма средств для помещения на счет рассчитывается исходя из среднего колебания курсов. Предположим, что это 0,09. Тогда сумма для размещения на счете будет равна 9000 долл. (100 000 × 0,0900 = 9000).
Сумма средств для помещения на счет рассчитывается исходя из среднего колебания курсов. Предположим, что это 0,09. Тогда сумма для размещения на счете будет равна 9000 долл. (100 000 × 0,0900 = 9000).
Далее в ход идет следующая схема хеджирования:
- Заключаем контракт. На валютном рынке покупаем (открываем позицию покупки) 100 000 евро без реальной поставки по текущему курсу доллара к евро 0,8500.
- Через месяц, когда товар получен, приобретаем 100 000 евро в банке по 0,8000 и перечисляем их поставщику. Т.к. на момент заключения сделки курс доллара по отношению к евро был больше, то прибыль составит 5000долл.
- Закрываем позицию на валютном рынке по 0,8000. Убыток от этого составит 5000долл.
Из примера видно, что убыток на депозитном счете компенсируется прибылью от конвертации евро в банке по лучшему курсу, чем в момент заключения контракта. Если бы курс изменился в другую сторону, то мы бы понесли убытки от покупки евро в банке, но при этом получили бы ровно такую же прибыль на валютном рынке.
Теперь можно сделать простой вывод – хеджирование это не способ заработка или получения прибыли. Целью хеджирования является исключительно снижение риска возможных потерь. Поэтому эффективность хеджирования можно оценивать только с учетом основной деятельности компании. Однако хорошая программа хеджирования может не только уменьшить риски, но и снизить затраты за счет высвобождения ресурсов компании.
Как разработать программу хеджирования рисков
Формирование программы хеджирования рисков всегда должно начинается с выявления этих рисков. Обычно функции риск-менеджера возлагаются на финансового директора и ему достаточно будет проанализировать, в каких валютах будут идти выплаты и поступления средств и каково их соотношение. Если пропорции будут не равными — компания скорее всего будет нести валютные риски.
Величина валютного риска зависит от разницы между объемами входящих и исходящих платежей в иностранной валюте, что так же еще называют величиной открытой валютной позиции. Если объемы доходов и расходов равны, валютная позиция называется закрытой. Если компания получает в валюте больше, чем платит, позиция считается открытой и называется длинной, если получает меньше, чем платит – позиция называется короткой.
Если объемы доходов и расходов равны, валютная позиция называется закрытой. Если компания получает в валюте больше, чем платит, позиция считается открытой и называется длинной, если получает меньше, чем платит – позиция называется короткой.
Открытая валютная позиция рассчитывается на основании запланированных бюджетом валютных платежей и поступлений.
После определения валютной позиции рассчитывается максимально возможные потери. Обычно для определения размера возможных потерь используется показатель VaR — Value at Risk. Этот показатель дает понять какие потери могут быть понесены с заданной долей вероятности. Нам вычисление этого показателя потребуется, чтобы понять, а надо ли вообще применять хеджирование или не стоит? Почему: как правило в компании устанавливается максимальный порог возможных потерь, которые компания может понести без значительного ущерба для основной деятельности. И проще, если этот порог будет выражен как процент от выручки или прибыли компании. Например, порог установлен в 5% от прибыли. Это значит, что компания готова потерять на изменении курса валют 5% от прибыли. Соответственно, все потери выше 5% должны хеджироваться (или применяются иные меры для снижения рисков).
Например, порог установлен в 5% от прибыли. Это значит, что компания готова потерять на изменении курса валют 5% от прибыли. Соответственно, все потери выше 5% должны хеджироваться (или применяются иные меры для снижения рисков).
VaR рассчитывается по формуле:
VaR = (Zα × σ — μ) × В × К
Где:
• μ — среднее значение ежедневного изменения курса валюты за период
• σ — стандартное отклонение ежедневного изменения курса валюты за период
• Zα — коэффициент, показывающий как изменяются потери относительно стандартного отклонения для заданной вероятности. Обычно для уровня достоверности в 95% используют значение 1,65, а для уровня достоверности 99% — 2,33. Что значит вероятность 95%? Это значит, что в 5% всех случаев потери компании могут быть больше полученной цифры. Это достаточно малая величина, поэтому 95% используется чаще всего. Мы этот коэффициент будем рассчитывать на основании заданного процента вероятности.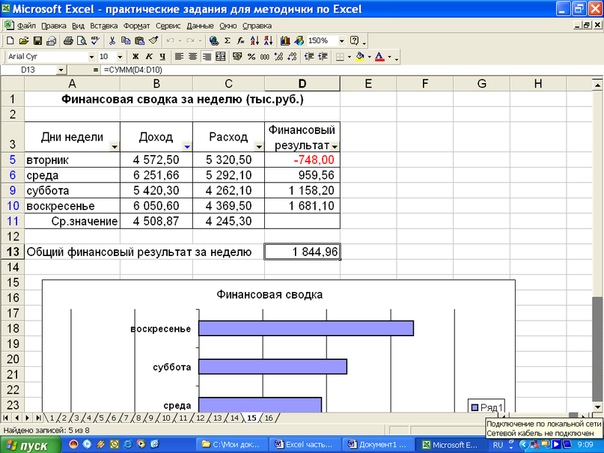 Т.е. достаточно будет ввести любой процент, а коэффициент будет рассчитан автоматически.
Т.е. достаточно будет ввести любой процент, а коэффициент будет рассчитан автоматически.
• В — величина открытой валютной позиции (доллары, евро и т.д.)
• К — курс валюты, установленный Центробанком на дату расчета риска
С теорией разобрались, теперь осталось все это перенести в Excel, чтоб нам осталось только забивать исходные данные, а Excel с помощью формул рассчитал две вещи:
- Какие возможные риски нас ожидают на заданный период. Если они не превышают установленный порог (в нашем случае это 5%), то хеджирование не применяем. Если превышают – следовательно необходимо рассмотреть возможность хеджирования.
- Какую минимальную сумму необходимо расположить на депозите, чтобы применить схему хеджирования, приведенную выше.
Изначально нам необходимо выгрузить с сайта центробанка ежедневные курсы валют за последний месяц от текущей даты и при помощи простой формулы мы определим изменение курса по отношению к предыдущей дате:
в приложенной к статье модели даты рассчитываются от текущей даты(при помощи функции СЕГОДНЯ(TODAY), а курс доллара записан фиксированный. Но ниже таблицы дат, в ячейках A28:C28, записана дата и пользовательская функция ЦБР для расчета курса валют. Эту функцию можно записать во все ячейки напротив дат и курс будет рассчитываться автоматически для этих дат при открытии файла.
Но ниже таблицы дат, в ячейках A28:C28, записана дата и пользовательская функция ЦБР для расчета курса валют. Эту функцию можно записать во все ячейки напротив дат и курс будет рассчитываться автоматически для этих дат при открытии файла.
На самом деле лучше брать период, равный периоду расчета рисков, но для примера возьмем данные за месяц.
Теперь надо определить значение среднего изменения курса за весь период и стандартное отклонение, на основании вычисленных изменений курса. Результаты будут записаны в отдельных ячейках. Для вычисления среднего используем функцию СРЗНАЧ(C2:C25), а для стандартного отклонения =СТАНДОТКЛОН(C2:C25):
Далее необходимо задать остальные исходные данные, которые помогут нам определить риски и дать ответ на вопрос: надо ли применять хеджирование?
Дату расчета рисков, Курс валюты на эту дату, Сумму открытой позиции, Уровень достоверности и Порог допустимых рисков укажем вручную. Уровень достоверности возьмем 95%, как наиболее оптимальный и часто используемый в таких случаях. А порог допустимых рисков укажем как 5% от прибыли.
А порог допустимых рисков укажем как 5% от прибыли.
Коэффициент рассчитаем по формуле =НОРМСТОБР(F8), где F8 – ячейка с уровнем достоверности. Это значит, что уровень достоверности мы сможем менять в любом направлении, а коэффициент при этом будет рассчитываться сам:
Теперь рассчитаем VaR, но перенесем формулу в Excel, используя имеющиеся входные параметры:
=(F9*(F2/100)-(F3/100))*F7*F6
Формулу можно записать и без множества дополнительных ячеек:
=(НОРМСТОБР(95%)*(СТАНДОТКЛОН(C2:C25)/100)-(СРЗНАЧ(C2:C25)/100))*100 000*62,098
Но в таком виде моделью будет неудобно пользоваться при изменении входных данных и сложнее анализировать причину результата, если он покажется подозрительным.
Так же добавим формулу, которая покажет нужно ли хеджирование (основываясь на порог допустимого риска):
=ЕСЛИ(F13>F7*F10;»ДА»;»НЕТ»)
И формулу, которая рассчитает минимальную сумму для вложения на депозит, если хеджирование нужно:
=ЕСЛИ(F14=»ДА»;F7*-F3;0)
В итоге получим такую модель:
На этой модели все наглядно и прозрачно, она позволяет сразу оценить вероятные риски и принять правильное решение относительно распределения ресурсов и стратегии снижения рисков.
Скачать файл с готовой моделью:
Модель хеджирования.xls (53,5 KiB, 878 скачиваний)
Статья помогла? Поделись ссылкой с друзьями! Видеоуроки
Поиск по меткам
Access apple watch Multex Power Query и Power BI VBA управление кодами Бесплатные надстройки Дата и время Записки ИП Надстройки Печать Политика Конфиденциальности Почта Программы Работа с приложениями Разработка приложений Росстат Тренинги и вебинары Финансовые Форматирование Функции Excel акции MulTEx ссылки статистикаФункция ДИСП — Служба поддержки Office
Оценивает дисперсию по выборке.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция ДИСП.В.
Синтаксис
ДИСП(число1;[число2];…)
Аргументы функции ДИСП описаны ниже.
-
Число1 Обязательный. Первый числовой аргумент, соответствующий выборке из генеральной совокупности.
-
Число2… Необязательный.
 Числовые аргументы 2—255, соответствующие выборке из генеральной совокупности.
Числовые аргументы 2—255, соответствующие выборке из генеральной совокупности.
Замечания
-
В функции ДИСП предполагается, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, для вычисления дисперсии следует использовать функцию ДИСПР.
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
-
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.

-
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
-
Чтобы включить логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию ДИСПА.
-
Функция ДИСП вычисляется по следующей формуле:
где x — выборочное среднее СРЗНАЧ(число1,число2,…), а n — размер выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Прочность | ||
|---|---|---|
|
1345 |
||
|
1301 |
||
|
1368 |
||
|
1322 |
||
|
1310 |
||
|
1370 |
||
|
1318 |
||
|
1350 |
||
|
1303 |
||
|
1299 |
||
|
Формула |
Описание |
Результат |
|
=ДИСП(A2:A11) |
Дисперсия предела прочности для всех протестированных инструментов. |
754,2667 |
Управление рисками
Построение модели потребительских рисков (кредитный скоринг) удобно начинать в приложении Binning Explorer. Binning Explorer позволяет интерактивно исследовать численные параметры характеризующих заемщиков, а также автоматизировать предобработку создания скоринговых карт. Binning Explorer позволяет:
- Импортировать данные;
- Изменять тип предиктора;
- Изменять разбиение алгоритма на один или более предикторов;
- Изменять параметры алгоритма для алгоритмов биннинга;
- Разделять бины по численным предикторам;
- Разделять бины по категориалым предикторам;
- Объединять вручную бины для объединения бинов числовых или категориальных предикторов;
- Изменять границы бина для одного предиктора;
- Изменять границы бина для нескольких предикторов;
- Настраивать параметры отображения;
- Экспортировать и сохранять бины.

После выполнения настройки бинов можно использовать как классический подход подбора модели кредитного скоринга на основе логистической регрессии, так и использовать методы машинного и глубокого обучения.
Машинное обучение, в отличие от методов подбора линейных моделей, представляет собой набор нелинейных методов, возможность применимости которых определяется путем численного эксперимента.
Наиболее рациональный способ выбора оптимальной модели в среде MATLAB — использование приложения Classification Learner App.
Более подробно рабочий процесс машинного обучения описан здесь.
Глубокое обучение — это наиболее современные методы построения моделей, основанных на глубоких нейронных сетях. Для создания скоринговых карт можно использовать различные архитектуры, основанные как на свёрточных, так и на рекуррентных нейронных сетях. Основное условие для создания модели нейронных сетей — достаточно большая обучаемая выборка. Конфигурацию сети можно собирать в виде кода или использовать интерактивный инструмент Deep Networks Designer, из которого, в свою очередь, можно получить как m код, так и объект модели сети.
Конфигурацию сети можно собирать в виде кода или использовать интерактивный инструмент Deep Networks Designer, из которого, в свою очередь, можно получить как m код, так и объект модели сети.
Видео:
Credit Scorecard Modeling Using the Binning Explorer App
Ссылка на документацию
Оценка инвестиционных проектов с применением MsExcel
Программа:
Теоретические основы инвестиционных проектов. Виды, классификации инвестиций.
2. Концепция временной стоимости денег. Текущая стоимость (PV), будущая стоимость (FV). Простые и сложные проценты. Ставка дисконтирования. Аннуитет. Prenumerando, postnumerando.
3. Денежный поток. Классификации ДП. ДП от текущей, инвестиционной и финансовой деятельности. ЧДП, настоящий и будущий денежные потоки.
4. Оценка финансовых инвестиций. Государственные и корпоративные облигации. Текущая стоимость облигаций (консольные, купонные с конечным сроком погашения, бескупонные с конечным сроком погашения). Акции (привилегированные, с потоком дивидендов, с постоянным темпом прироста дивидендов).
Акции (привилегированные, с потоком дивидендов, с постоянным темпом прироста дивидендов).
5. Принципы и схема оценки инвестиционных проектов. Статические и динамические методы (NPV, PI, IRR, PBP. Точка Фишера).
6. Риск и доходность. Безрисковый эквивалент СЕ (certainly equivalent). Ожидаемая доходность. Риск ожидаемой доходности- СКО, вариация. Модель Шарпа для оценки доходности акции. Характеристическая линия. Модель арбитражного ценообразования (Фама, Росс).
7. Методология оценки инвестиционных проектов: компьютерный практикум. Программный продукт MS Excel. Оценка будущих и приведенных сумм инвестиций, платежей ренты. Расчеты с учетом инфля-ции. Применение MS Excel для расчета инвестиционных проектов. Функции MS Excel: ПС (PV), БС (FV), ПЛТ (PMT), ЧПС (NPV), ВСД (IRR). Особенности их применения. Вычисление размера погашающего платежа с разделением на части (выплаты по процентам и по основному долгу). Функции MS Excel: ПРПЛТ и ОСПЛТ. Оценка инвестиционных проектов, денежные потоки которых, не носят периодический характер. Функции MS Excel: ЧИСТНЗ и ЧИСТВНДОХ.
Функции MS Excel: ЧИСТНЗ и ЧИСТВНДОХ.
8. Риск инвестиционного проекта. Дерево вероятностей. Начальная, условная, совместная вероятности. Ожидаемое NPV. СКО и вариация NPV. Метод Монте-Карло. Расчеты в Excel.
9. Неопределенность и риск. Виды рисков. Показатели доходности и риска при инвестировании в ценные бумаги. Риск инвестиций. Измерение риска. Соотношение доходности и риска. Расчеты в Excel.
10. Инвестиционные портфели. Принцип формирования инвестиционных портфелей. Доходность и риск инвестиционного портфеля. Теория диверсификации Марковица. Определение оптимального инвестиционного портфеля. Расчеты в Excel.
11. Оптимизация инвестирования. Использование концепции рисковой стоимости (Value at Risk — VAR) для оценки эффективности инвестиционных проектов. Модели и критерии оптимального отбора. Сравнение инвестиционных проектов разной продолжительности. Критические точки и анализ чувствительности инвестиционного проекта. Метод сценариев. Моделирование и прогнозирование денежных потоков по проекту. Итоговый СaseStudy на персональных компьютерах.
Итоговый СaseStudy на персональных компьютерах.
Дисперсия и стандартное отклонение в EXCEL. Примеры и описание
Вычислим в MS EXCEL дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.
Сначала рассмотрим дисперсию , затем стандартное отклонение .
Дисперсия выборки
Дисперсия выборки ( выборочная дисперсия, sample variance ) характеризует разброс значений в массиве относительно среднего .
Все 3 формулы математически эквивалентны.
Из первой формулы видно, что дисперсия выборки это сумма квадратов отклонений каждого значения в массиве от среднего , деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления дисперсии выборки используется функция
ДИСП()
, англ. 2)/ (СЧЁТ(Выборка)-1
) –
формула массива
2)/ (СЧЁТ(Выборка)-1
) –
формула массива
Дисперсия выборки равна 0, только в том случае, если все значения равны между собой и, соответственно, равны среднему значению . Обычно, чем больше величина дисперсии , тем больше разброс значений в массиве.
Дисперсия выборки является точечной оценкой дисперсии распределения случайной величины, из которой была сделана выборка . О построении доверительных интервалов при оценке дисперсии можно прочитать в статье Доверительный интервал для оценки дисперсии в MS EXCEL .
Дисперсия случайной величины
Чтобы вычислить дисперсию случайной величины, необходимо знать ее функцию распределения .
Для дисперсии случайной величины Х часто используют обозначение Var(Х). Дисперсия равна математическому ожиданию квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X)) 2 ]
Если случайная величина имеет дискретное распределение , то дисперсия вычисляется по формуле:
где x i – значение, которое может принимать случайная величина, а μ – среднее значение (
математическое ожидание случайной величины
), р(x) – вероятность, что случайная величина примет значение х.
Если случайная величина имеет непрерывное распределение , то дисперсия вычисляется по формуле:
где р(x) – плотность вероятности .
Для распределений, представленных в MS EXCEL , дисперсию можно вычислить аналитически, как функцию от параметров распределения. Например, для Биномиального распределения дисперсия равна произведению его параметров: n*p*q.
Примечание : Дисперсия, является вторым центральным моментом , обозначается D[X], VAR(х), V(x). Второй центральный момент — числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно математического ожидания .
Примечание : О распределениях в MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Размерность дисперсии соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг 2 . Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из дисперсии – стандартное отклонение .
Некоторые свойства дисперсии :
Var(Х+a)=Var(Х), где Х — случайная величина, а — константа.
Var(aХ)=a 2 Var(X)
Var(Х)=E[(X-E(X)) 2 ]=E[X 2 -2*X*E(X)+(E(X)) 2 ]=E(X 2 )-E(2*X*E(X))+(E(X)) 2 =E(X 2 )-2*E(X)*E(X)+(E(X)) 2 =E(X 2 )-(E(X)) 2
Это свойство дисперсии используется в статье про линейную регрессию .
Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y — случайные величины, Cov(Х;Y) — ковариация этих случайных величин.
Если случайные величины независимы (independent), то их ковариация равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе стандартной ошибки среднего .
Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1) 2 Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения доверительного интервала для разницы 2х средних .
Примечание : квадратный корень из дисперсии случайной величины называется Среднеквадратическое отклонение (или другие названия — среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение, стандартное отклонение, стандартный разброс).
Стандартное отклонение выборки
Стандартное отклонение выборки — это мера того, насколько широко разбросаны значения в выборке относительно их среднего .
По определению, стандартное отклонение равно квадратному корню из дисперсии :
Стандартное отклонение не учитывает величину значений в выборке , а только степень рассеивания значений вокруг их среднего . Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется Коэффициент вариации (Coefficient of Variation, CV) — отношение Стандартного отклонения к среднему арифметическому , выраженного в процентах.
В MS EXCEL 2007 и более ранних версиях для вычисления Стандартного отклонения выборки используется функция =СТАНДОТКЛОН() , англ.2)/(СЧЁТ(Выборка)-1))
Другие меры разброса
Функция КВАДРОТКЛ() вычисляет с умму квадратов отклонений значений от их среднего . Эта функция вернет тот же результат, что и формула =ДИСП.Г( Выборка )*СЧЁТ( Выборка ) , где Выборка — ссылка на диапазон, содержащий массив значений выборки ( именованный диапазон ). Вычисления в функции КВАДРОТКЛ() производятся по формуле:
Функция СРОТКЛ() является также мерой разброса множества данных. Функция СРОТКЛ() вычисляет среднее абсолютных значений отклонений значений от среднего . Эта функция вернет тот же результат, что и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка) , где Выборка — ссылка на диапазон, содержащий массив значений выборки.
Вычисления в функции СРОТКЛ () производятся по формуле:
Как посчитать вариацию в excel. Функции расчета стандартного отклонения в Excel. Практическое воплощение в Excel
Среди множества показателей, которые применяются в статистике, нужно выделить расчет дисперсии. Следует отметить, что выполнение вручную данного вычисления – довольно утомительное занятие. К счастью, в приложении Excel имеются функции, позволяющие автоматизировать процедуру расчета. Выясним алгоритм работы с этими инструментами.
Дисперсия – это показатель вариации, который представляет собой средний квадрат отклонений от математического ожидания. Таким образом, он выражает разброс чисел относительно среднего значения. Вычисление дисперсии может проводиться как по генеральной совокупности, так и по выборочной.
Способ 1: расчет по генеральной совокупности
Для расчета данного показателя в Excel по генеральной совокупности применяется функция ДИСП.Г . Синтаксис этого выражения имеет следующий вид:
ДИСП.Г(Число1;Число2;…)
Всего может быть применено от 1 до 255 аргументов. В качестве аргументов могут выступать, как числовые значения, так и ссылки на ячейки, в которых они содержатся.
Посмотрим, как вычислить это значение для диапазона с числовыми данными.
Способ 2: расчет по выборке
В отличие от вычисления значения по генеральной совокупности, в расчете по выборке в знаменателе указывается не общее количество чисел, а на одно меньше. Это делается в целях коррекции погрешности. Эксель учитывает данный нюанс в специальной функции, которая предназначена для данного вида вычисления – ДИСП.В. Её синтаксис представлен следующей формулой:
ДИСП.В(Число1;Число2;…)
Количество аргументов, как и в предыдущей функции, тоже может колебаться от 1 до 255.
Как видим, программа Эксель способна в значительной мере облегчить расчет дисперсии. Эта статистическая величина может быть рассчитана приложением, как по генеральной совокупности, так и по выборке. При этом все действия пользователя фактически сводятся только к указанию диапазона обрабатываемых чисел, а основную работу Excel делает сам. Безусловно, это сэкономит значительное количество времени пользователей.
Одним из основных инструментов статистического анализа является расчет среднего квадратичного отклонения. Данный показатель позволяет сделать оценку стандартного отклонения по выборке или по генеральной совокупности. Давайте узнаем, как использовать формулу определения среднеквадратичного отклонения в Excel.
Сразу определим, что же представляет собой среднеквадратичное отклонение и как выглядит его формула. Эта величина является корнем квадратным из среднего арифметического числа квадратов разности всех величин ряда и их среднего арифметического. Существует тождественное наименование данного показателя — стандартное отклонение. Оба названия полностью равнозначны.
Но, естественно, что в Экселе пользователю не приходится это высчитывать, так как за него все делает программа. Давайте узнаем, как посчитать стандартное отклонение в Excel.
Расчет в Excel
Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.
Способ 1: мастер функций
Способ 2: вкладка «Формулы»
Способ 3: ручной ввод формулы
Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.
Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.
В данной статье я расскажу о том, как найти среднеквадратическое отклонение . Этот материал крайне важен для полноценного понимания математики, поэтому репетитор по математике должен посвятить его изучению отдельный урок или даже несколько. В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.
Среднеквадратическое отклонение дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом (греческая буква «сигма»).
Формула для расчета довольно проста. Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии. Так что теперь вы должны спросить: “А что же такое дисперсия?”
Что такое дисперсия
Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.
Чтобы найти дисперсию последовательно проведите следующие вычисления:
- Определите среднее (простое среднее арифметическое ряда значений).
- Затем от каждого из значений отнимите среднее и возведите полученную разность в квадрат (получили квадрат разности ).
- Следующим шагом будет вычисление среднего арифметического полученных квадратов разностей (Почему именно квадратов вы сможете узнать ниже).
Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.
Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.
Сперва найдём среднее значение . Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:
Среднее мм.
Итак, среднее (среднеарифметическое) составляет 394 мм.
Теперь нужно определить отклонение роста каждой из собак от среднего :
Наконец, чтобы вычислить дисперсию , каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:
Дисперсия мм 2 .
Таким образом, дисперсия составляет 21704 мм 2 .
Как найти среднеквадратическое отклонение
Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:
Мм (округлено до ближайшего целого значения в мм).
Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).
Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.
То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.
Что такое стандартное отклонение
Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.
Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.
Если есть значений, то:
Все остальные расчеты производятся аналогично, в том числе и определение среднего.
Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:
Дисперсия выборки = мм 2 .
При этом стандартное отклонение по выборке равно мм (округлено до ближайшего целого значения).
Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.
Примечание. Почему именно квадраты разностей?
Но почему при вычислении дисперсии мы берём именно квадраты разностей? Допустим при измерении какого-то параметра, вы получили следующий набор значений: 4; 4; -4; -4. Если мы просто сложим абсолютные отклонения от среднего (разности) между собой … отрицательные значения взаимно уничтожатся с положительными:
.
Получается, этот вариант бесполезен. Тогда, может, стоит попробовать абсолютные значения отклонений (то есть модули этих значений)?
На первый взгляд получается неплохо (полученная величина, кстати, называется средним абсолютным отклонением), но не во всех случаях. Попробуем другой пример. Пусть в результате измерения получился следующий набор значений: 7; 1; -6; -2. Тогда среднее абсолютное отклонение равно:
Вот это да! Снова получили результат 4, хотя разности имеют гораздо больший разброс.
А теперь посмотрим, что получится, если возвести разности в квадрат (и взять потом квадратный корень из их суммы).
Для первого примера получится:
.
Для второго примера получится:
Теперь – совсем другое дело! Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности … к чему мы и стремились.
Фактически в данном методе использована та же идея, что и при вычислении расстояния между точками, только примененная иным способом.
И с математической точки зрения использование квадратов и квадратных корней дает больше пользы, чем мы могли бы получить на основании абсолютных значений отклонений, благодаря чему среднеквадратическое отклонение применимо и для других математических задач.
О том, как найти среднеквадратическое отклонение, вам рассказал , Сергей Валерьевич
Вычислим в MS EXCEL дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.
Сначала рассмотрим дисперсию , затем стандартное отклонение .
Дисперсия выборки
Дисперсия выборки (выборочная дисперсия, sample variance ) характеризует разброс значений в массиве относительно .
Все 3 формулы математически эквивалентны.
Из первой формулы видно, что дисперсия выборки это сумма квадратов отклонений каждого значения в массиве от среднего , деленная на размер выборки минус 1.2)/ (СЧЁТ(Выборка)-1 ) –
Дисперсия выборки равна 0, только в том случае, если все значения равны между собой и, соответственно, равны среднему значению . Обычно, чем больше величина дисперсии , тем больше разброс значений в массиве.
Дисперсия выборки является точечной оценкой дисперсии распределения случайной величины, из которой была сделана выборка . О построении доверительных интервалов при оценке дисперсии можно прочитать в статье .
Дисперсия случайной величины
Чтобы вычислить дисперсию случайной величины, необходимо знать ее .
Для дисперсии случайной величины Х часто используют обозначение Var(Х). Дисперсия равна квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X)) 2 ]
дисперсия вычисляется по формуле:
где x i – значение, которое может принимать случайная величина, а μ – среднее значение (), р(x) – вероятность, что случайная величина примет значение х.
Если случайная величина имеет , то дисперсия вычисляется по формуле:
Размерность дисперсии соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг 2 . Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из дисперсии – стандартное отклонение .
Некоторые свойства дисперсии :
Var(Х+a)=Var(Х), где Х — случайная величина, а — константа.
Var(aХ)=a 2 Var(X)
Var(Х)=E[(X-E(X)) 2 ]=E=E(X 2)-E(2*X*E(X))+(E(X)) 2 =E(X 2)-2*E(X)*E(X)+(E(X)) 2 =E(X 2)-(E(X)) 2
Это свойство дисперсии используется в статье про линейную регрессию .
Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y — случайные величины, Cov(Х;Y) — ковариация этих случайных величин.
Если случайные величины независимы (independent), то их ковариация равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе .
Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1) 2 Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения .
Стандартное отклонение выборки
Стандартное отклонение выборки — это мера того, насколько широко разбросаны значения в выборке относительно их .
По определению, стандартное отклонение равно квадратному корню из дисперсии :
Стандартное отклонение не учитывает величину значений в выборке , а только степень рассеивания значений вокруг их среднего . Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется Коэффициент вариации (Coefficient of Variation, CV) — отношение Стандартного отклонения к среднему арифметическому , выраженного в процентах.2)/(СЧЁТ(Выборка)-1))
Другие меры разброса
Функция КВАДРОТКЛ() вычисляет сумму квадратов отклонений значений от их среднего . Эта функция вернет тот же результат, что и формула =ДИСП.Г(Выборка )*СЧЁТ(Выборка ) , где Выборка — ссылка на диапазон, содержащий массив значений выборки (). Вычисления в функции КВАДРОТКЛ() производятся по формуле:
Функция СРОТКЛ() является также мерой разброса множества данных. Функция СРОТКЛ() вычисляет среднее абсолютных значений отклонений значений от среднего . Эта функция вернет тот же результат, что и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка) , где Выборка — ссылка на диапазон, содержащий массив значений выборки.
Вычисления в функции СРОТКЛ () производятся по формуле:
Необходимо вмешательство менеджмента для выявления причин отклонений.
Для построения контрольной карты я использую исходные данные, среднее значение (μ) и стандартное отклонение (σ). В Excel: μ = СРЗНАЧ($F$3:$F$15), σ = СТАНДОТКЛОН($F$3:$F$15)
Сама контрольная карта включает: исходные данные, среднее значение (μ), нижнюю контрольную границу (μ – 2σ) и верхнюю контрольную границу (μ + 2σ):
Скачать заметку в формате , примеры в формате
Посмотрев на представленную карту, я заметил, что исходные данные демонстрируют вполне различимую линейную тенденцию к снижению доли накладных расходов:
Чтобы добавить линию тренду выделите на графике ряд с данными (в нашем примере – зеленые точки), кликните правой кнопкой мыши и выберите опцию «Добавить линию тренда». В открывшемся окне «Формат линии тренда», поэкспериментируйте с опциями. Я остановился на линейном тренде.
Если исходные данные не разбросаны в соответствии с вокруг среднего значения, то описывать их параметрами μ и σ не вполне корректно. Для описания вместо среднего значения лучше подойдет прямая линейного тренда и контрольные границы, равноудаленные от этой линии тренда.
Линию тренда Excel позволяет построить с помощью функции ПРЕДСКАЗ.2)/(СЧЁТЗ($F$3:$F$15)-1))
необходимо нажать не Enter, а Ctrl + Shift + Enter. Не пытайтесь ввести фигурные скобки с клавиатуры – формула массива не заработает. Если требуется отредактировать формулу массива, сделайте это так же, как и с обычной формулой, но опять же по окончании редактирования нажмите не Enter, а Ctrl + Shift + Enter.
Формулу массива, возвращающую одно значение, можно «протаскивать», как и обычную формулу.
В результате получили контрольную карту, построенную для данных, имеющих тенденцию к понижению
P.S. После того, как заметка была написана, я смог усовершенствовать формулы, используемые для вычисления стандартного отклонения для данных с тенденцией. Ознакомиться с ними вы можете в Excel-файле
Расчет стоимости, подверженной риску, в Excel и Python
Автор: Вибху Сингх
Что я могу больше всего потерять от этих инвестиций? Это вопрос, который задает каждый инвестор, который инвестировал в определенный момент времени. Value at Risk (VaR) пытается дать ответ. В этом блоге мы понимаем и вычисляем VaR в Excel и Python с использованием исторического метода и подхода дисперсии-ковариации.
VaR был разработан в середине 1990-х годов в ответ на различные финансовые кризисы, но истоки мер уходят далеко в прошлое.
По словам Филиппа Жориона, «VaR измеряет наихудшие ожидаемые убытки на заданном горизонте при нормальных рыночных условиях при заданном уровне уверенности».
Это определение подразумевает, что необходимо выбрать два параметра, а именно период удержания и уровень достоверности. Обычно уровень достоверности находится в диапазоне от 90% до 99%, например 90%, 95%, 99%. Срок владения может варьироваться от суток до года.
Предположим, аналитик говорит, что однодневная VaR портфеля составляет 1 миллион долларов с уровнем достоверности 95%.Это означает, что существует 95% -ная вероятность того, что максимальные потери не превысят 1 миллион долларов за один день. Другими словами, вероятность того, что убытки портфеля в конкретный день превысят 1 миллион долларов, составляет всего 5%.
Существуют различные методы расчета VaR. В этом блоге мы обсуждаем вариационно-ковариационный подход и метод исторического моделирования.
Начнем с подхода отклонения-ковариации .
Ковариация дисперсии — это параметрический метод, который предполагает, что доходность распределена нормально.В этом методе мы сначала вычисляем среднее значение и стандартное отклонение доходности. Для уровня достоверности 95% VaR рассчитывается как среднее значение -1,65 * стандартное отклонение, а для уровня достоверности 99% VaR рассчитывается как -2,33 * стандартное отклонение.
Расчет VaR в Excel с использованием подхода дисперсия-ковариация- Импорт данных из Yahoo finance
- Рассчитайте доходность цены закрытия Возврат = Сегодняшняя цена — Вчерашняя цена / Вчерашняя цена
- Рассчитайте среднее значение доходность с использованием среднего значения функция
- Вычислите стандартное отклонение доходности с помощью функции СТАНДОТКЛОН
- Наконец, мы вычисляем VaR для уровней достоверности 90, 95 и 99, используя NORM.Функция INV . Эта функция имеет три параметра: вероятность, среднее значение и стандартное отклонение. Вероятно, мы используем 0,1, 0,05, 0,01 соответственно для VaR (90), VaR (95) и VaR (99)
1. Импортируем необходимые библиотеки
2. Импортируйте ежедневные данные об акциях Facebook из Yahoo Finance и рассчитайте дневную доходность
3. Определите среднее значение и стандартное отклонение дневной доходности.Постройте нормальную кривую против дневной доходности
4. Рассчитайте VaR, используя функцию точечного процентиля
Выход:
Подход исторического моделированияисторический метод в Excel выглядит следующим образом:
- Подобно подходу дисперсии-ковариации, сначала мы вычисляем доходность акции. Возврат = сегодняшняя цена — вчерашняя цена / вчерашняя цена
- Сортируем доходность от худшей к лучшей.
- Затем мы вычисляем общее количество возвратов с помощью функции count .
- VaR (90) — это отсортированный доход, соответствующий 10% от общего количества.
- Аналогично, VaR (95) и VaR (99) — это отсортированный доход, соответствующий 5% и 1% от общего количества соответственно.
Python:
1. Импортируйте необходимые библиотеки
2. Рассчитайте дневную доходность
3.Сортировка результатов
4. Рассчитайте VaR для уровней достоверности 90%, 95% и 99%, используя функцию квантиля.
Вывод:
Как видите, разница между стоимость, подверженная риску, рассчитанная на основе исторического моделирования и вариационно-ковариационного подхода. Это говорит нам о том, что распределение доходности не является нормальным.
ЗаключениеНа этом я заканчиваю этот блог, но есть еще один подход к вычислению VaR.Если вам интересно, вы можете ознакомиться с курсами опционов на Quantra, которые охватывают различные стратегии торговли опционами с методами управления рисками.
Скачать файл данных- Расчет VaR в excel.xlsx
- Value + at + Risk.ipynb
Войти для загрузки
Update
Мы заметили, что некоторые пользователи сталкиваются с проблемами при загрузке рыночные данные с платформ Yahoo и Google Finance.Если вы ищете альтернативный источник рыночных данных, вы можете использовать для этого Quandl.
Заявление об ограничении ответственности: все инвестиции и торговля на фондовом рынке сопряжены с риском. Любые решения о размещении сделок на финансовых рынках, включая торговлю акциями, опционами или другими финансовыми инструментами, являются личным решением, которое должно приниматься только после тщательного исследования, включая личный риск и финансовую оценку, а также привлечение профессиональной помощи в той степени, в которой вы считаю необходимым.Торговые стратегии или соответствующая информация, упомянутые в этой статье, предназначены только для информационных целей.
Рассчитайте стоимость под риском в Excel
Сегодня я хотел бы прояснить концепцию Value at Risk . Я продемонстрирую, как можно рассчитать VAR в Excel, но также остановлюсь на некоторых его ограничениях.
Value at Risk, или VaR, как его обычно называют, — это мера риска, которая отвечает на вопрос «Каковы мои потенциальные убытки». В частности, это потенциальные убытки портфеля при заданном доверительном интервале за определенный период.VAR состоит из трех важных частей.
- Уровень достоверности. Обычно это 95% или 99%.
- Период времени. Это может быть день, месяц или год.
- Ваш потенциальный убыток за выбранный период времени при заданном уровне достоверности при нормальных рыночных условиях (о финальной квалификации часто забывают!)
Существует несколько подходов к расчету стоимости, подверженной риску, но здесь я рассмотрю самый простой (здесь описаны другие методы, включая моделирование Монте-Карло и методы дельта-гаммы).
Расчет стоимости, подверженной риску на основе нормального распределенияСначала вам нужно указать несколько параметров, как показано на рисунке 1.
- Стоимость вашего портфеля
- Средняя доходность за один период времени (это может быть более дня, месяца или года)
- Стандартное отклонение доходности за один период времени
- Желаемый уровень достоверности
| Рисунок 1 |
Теперь выполните вычисления как указанное на рисунке 2
| Рисунок 2 |
- Рассчитайте минимальную ожидаемую доходность по отношению к уровню уверенности (т.е. если ваш уровень уверенности составляет 99%, то вы на 99% уверены, что ваша доходность будет выше этого значения). Это делается с помощью функции Excel NORM.INV ().
- Рассчитайте минимальную ожидаемую доходность (при заданном уровне достоверности)
- Теперь вычислите стоимость, подверженную риску за один период времени
Теперь ваша стоимость подвергается риску в течение одного периода времени. Допустим, период времени — один день. Чтобы преобразовать значение, подверженное риску за один день, в соответствующее значение за месяц, вам просто нужно умножить значение, подверженное риску, на квадратный корень из количества торговых дней в месяце.Если в месяце 22 торговых дня, то
Ценность, подверженная риску в течение месяца = Ценность, подверженная риску в течение дня x √ 22
Ограничения и недостатки стоимости, подверженной рискуЕсть два основных ограничения на использование VaR в качестве меры риска.
VaR — не худший вариант убытка . При уровне достоверности 95% VaR — это ваш минимальный ожидаемый убыток в 5% случаев. Это не ваш максимальный ожидаемый убыток. Это наиболее часто игнорируемое ограничение, которое может привести к ложному чувству безопасности.Фактические убытки за эти 5% торговых дней могут составить всего несколько долларов или достаточно, чтобы сокрушить вашу компанию.
VaR не обязательно действителен, если он вам нужен больше всего . VaR обычно предполагает, что доходность инвестиций имеет нормальное распределение, а инвестиционное поведение хорошо предсказуемо в конце. Но инвестиции, как правило, носят непонятный характер и не всегда распределяются по нормальному закону. Таким образом, обстоятельства, для которых VaR был разработан (т. Е. События, которые происходят не часто, но имеют большое влияние), представляют собой те обстоятельства, в которых эти предположения не верны.
Фактически, Дэвид Эйнхорн, президент Greenlight Capital заметил, что Value at Risk — это « подушка безопасности, которая работает все время, кроме случаев, когда вы попали в автомобильную аварию. »
Таким образом, Value At Risk должно быть только одним из нескольких используемых вами инструментов оценки риска.
Загрузить электронную таблицу для расчета стоимости, подверженной риску, в Excel
Value at Risk (VAR) Excel Example
Для версий Excel : Excel для Office 365, Excel для Office 365 для Mac, Excel 2016, Excel 2016 для Mac, Excel 2013, Excel 2011 для Mac, Excel 2010, Excel 2008 для Mac, Excel 2007
Пример таблицы Value at Risk в Excel
Value at Risk (VaR) — это статистическая мера риска ухудшения ситуации, применяемая к текущим позициям портфеля.Он представляет собой риск ухудшения ситуации в будущем на определенный период времени без изменения удерживаемых позиций. Однако VaR можно рассчитать для любого периода времени, поскольку неопределенность увеличивается со временем, он часто рассчитывается для одного дня или нескольких дней в будущем.
Методы VaR
Существует два основных метода расчета VaR:
- Использование исторических данных или эмпирических данных, называемых непараметрическими.
- Использование приближения, основанного на некотором теоретическом распределении вероятностей, таком как нормальное распределение.
Что должен делать VaR
Предполагается, чтоVaR представляет наихудший сценарий, при котором существует малая вероятность того, что фактические потери превысят рассчитанный VaR. Таким образом, для уровня достоверности 95% VaR представляет собой движение вниз на 1,645 SD, а для уровня достоверности 99% это представляет собой движение вниз на 2,33 SD. При вычислении VaR мы фактически вычисляем средний VaR на основе некоторого заранее заданного уровня достоверности. Недостатком является то, что невозможно оценить, насколько велики могут быть потери, если движение вниз превышает доверительный уровень.
Стоимость под риском Моделирование методом Монте-Карло в Excel
Включены два видеоурока, посвященных рискам, связанным с использованием Excel. Первый определяет VaR и демонстрирует расчет параметрического VaR детерминированно на основе исторического среднего и дисперсии. Во втором руководстве демонстрируется расчет стоимости, подверженной риску, с помощью моделирования Монте-Карло в Excel.
Вы можете скачать шаблон Excel, использованный в видео, здесь.
Параметрическая стоимость под риском — расчет VaR
Пармаметрическое значение при Rsik (VaR)
Стоимость под риском Метод Монте-Карло
VaR стоимости под риском с использованием Excel (с формулами MarketXLS)
Стоимость под риском с использованием Excel — один из наиболее важных финансовых инструментов, которые помогают инвестору измерить риск инвестиционного портфеля.В этой статье будет обсуждаться, что это такое, как он затем рассчитывается, как MarketXLS рассчитывает рисковую стоимость вашего портфеля.
Стоимость под риском — это статистическая мера рискованности портфелей активов. Он определяет уровень финансового риска в портфеле за определенный период времени. Value-At-Risk — это число, измеряемое в единицах цены или в процентах от стоимости портфеля, которое определяет большой процент случаев (обычно 95% или 99%) для портфеля, который, вероятно, не потеряет больше, чем это количество Деньги.
Для оценки вероятности убытка нам необходимо определить распределения вероятностей отдельных рисков с доверительным интервалом. Существует три жизненно важных элемента VaR:
1. Заданный уровень потери стоимости,
2. Фиксированный период, в течение которого оценивается риск
3. Доверительный интервал (заданное состояние рынка).
Исторический VaR
Историческая стоимость под риском (VaR), также известная как историческое моделирование или исторический метод, относится к определенному способу расчета VaR.В этом подходе мы рассчитываем VaR непосредственно на основе прошлой доходности.
Например, предположим, что мы хотим рассчитать 1-дневный 95% VaR для капитала, используя данные за 100 дней. 95-й процентиль соответствует 5% наименее плохих из наихудших результатов. В этом случае, поскольку мы используем данные за 100 дней, VaR просто соответствует 5-му наихудшему дню.
где:
VaR (1 — a) — это оценочная VaR с доверительной вероятностью 100 × (1 — a)%.
(Ra) — это среднее значение серии смоделированных доходов или прибылей и убытков портфеля.
Ra — это наихудшая доходность серии смоделированных прибылей и убытков портфеля или, другими словами, доходность набора смоделированных прибылей и убытков, соответствующая уровню значимости.
Условный VaR
Условная стоимость под риском (CVaR), также известная как ожидаемый дефицит, представляет собой меру оценки риска, которая количественно определяет величину остаточного риска инвестиционного портфеля. CVaR получается путем взятия средневзвешенного значения «экстремальных» убытков в хвосте распределения возможных прибылей за пределами точки отсечения значения, подверженного риску (VaR).Условная стоимость под риском используется при оптимизации портфеля для эффективного управления рисками.
Условная стоимость под риском (CVaR) пытается устранить недостатки модели VaR, которая представляет собой статистический метод, используемый для измерения уровня финансового риска внутри фирмы или инвестиционного портфеля в течение определенного периода времени.
CVaR — это ожидаемые убытки, если когда-либо будет превышен порог наихудшего случая. CVaR, другими словами, количественно оценивает ожидаемые потери, которые происходят после точки разрыва VaR.
Гауссов VaR
Этот метод предполагает, что доходность акций распределяется нормально. Для этого требуется, чтобы мы оценили только два фактора — ожидаемую (или среднюю) доходность и стандартное отклонение — которые позволяют нам построить кривую нормального распределения.
Поскольку доходность за разные периоды близка к некоррелированной, дисперсия доходности T-дня должна быть в T раз больше дисперсии доходности за 1 день. Следовательно, с точки зрения волатильности (или стандартного отклонения) стоимость под риском может быть скорректирована как:
VAR (T дней) = VAR (1 день) x SQRT (T)
Чтобы получить VaR для акции, мы умножаем пороговое значение на стандартное отклонение стоимости портфеля σ.VaR показан на следующем рисунке:
Нормальные распределения симметричны и полностью описываются двумя параметрами: средним значением и стандартным отклонением. Другое преимущество нормального распределения состоит в том, что средневзвешенное значение переменных, которые обычно распределены, также будет нормально распределено. Таким образом, разные акции с нормальным распределением можно комбинировать с другими акциями или ценными бумагами с нормальным распределением, и весь портфель будет нормально распределен.
Корниш Фишер VaR
Разложение Корниш-Фишера (CF) — это способ преобразования стандартной гауссовской случайной величины z в негауссовскую случайную величину Z. Методика расчета остается во многом аналогичной, только Z-балл корректируется следующим образом:
Где:
z = гауссовский z-показатель
S = перекос
K = избыточный эксцесс
Как MarketXLS рассчитывает рисковую стоимость вашего портфеля
MarketXLS® полностью автоматизирует процесс расчета использования Excel для получения оптимальных портфелей, которые, как правило, лежат на границе эффективности.
Инвестор должен ввести следующие данные:
1. Символ актива: введите тикер, под которым торгуется ценная бумага в вашем Портфеле.
2. Вес актива в вашем портфеле: введите процентный вес каждой ценной бумаги, как показано ниже.
Ввод:
Дополнительные поля:
Уровень значимости:
По умолчанию MarketXLS предполагает 5% -ный уровень значимости при отсутствии какого-либо пользовательского ввода.
Месяцев под наблюдением:
Чтобы определить, сколько месяцев вы хотите ретроспективно использовать для проведения расчетов, вы можете ввести количество месяцев, которое вы чувствуете лучше всего, учитывая, что все ценные бумаги в вашем портфеле существуют достаточно долго, чтобы иметь данные за эти периоды. Значение по умолчанию: при отсутствии каких-либо действий со стороны пользователя MarketXLS использует данные за предыдущие 12 месяцев с даты запроса.
Инвестор может использовать формулу «Value-at-risk of Portfolio excel», чтобы получить оценку для определения совокупных рисков в портфеле.Моделирование VaR определяет потенциальные убытки в оцениваемой организации и вероятность возникновения определенных убытков. Инвестор узнает о риске, связанном с портфелем, с помощью VaR с MarketXLS.
Ниже приводится краткое описание расчетов VaR в Excel с помощью MarketXLS
.Скачать презентацию можно здесь.
Загрузите шаблон портфолио здесь.
Подход исторического моделированияVaR — EXCEL
5 минут на чтениеВ этом посте мы рассчитаем стоимость под риском в EXCEL, используя подход исторического моделирования VaR.
1. Какая стоимость подвержена риску?
Возможно, самая простая и распространенная концепция, которую вы, вероятно, увидите, когда дело доходит до управления финансовыми рисками, — это стоимость под риском или сокращенно VaR. Он представляет собой обоснованную оценку для:
a) Насколько плохими могут стать цены, когда они действительно станут плохими? или
b) Что больше всего вы можете потерять в действительно плохой день из-за изменения цен? или
c) Что самое худшее, что может случиться, когда рынок достигнет свободного падения?
Несмотря на то, что VaR получил большое количество негативных отзывов после 2008 года, прежде чем мы обсудим проблемы, было бы полезно сначала определить, как рассчитать стоимость под риском.
Существует три метода расчета стоимости, подверженной риску. Ковариация дисперсии (VCV), историческое моделирование и моделирование методом Монте-Карло. В этом посте мы начнем с серии данных по обменному курсу доллара США к евро. Затем посмотрите, что показатель «Стоимость под риском» может рассказать нам о вероятном (наиболее частом) и наихудшем (экстремальном) движении этого обменного курса.
Мы рассчитаем стоимость, подверженную риску, используя метод исторического моделирования в EXCEL.
2.
Руководство по Va lue at Risk Подход к историческому моделированиюНапример, взгляните на следующую гистограмму EXCEL.
Расчет стоимости, подверженной риску — гистограмма — первый шаг в подходе исторического моделирования VaRЭта гистограмма рассчитывается с использованием серии ежедневных изменений цен для данной финансовой ценной бумаги. С точки зрения риска мы называем ежедневные изменения цен ежедневной доходностью, и эта доходность может быть положительной или отрицательной.
Приведенная выше гистограмма берет серию ежедневных доходностей, сортирует ряды и затем помещает каждый доход в заданный период возврата.
а. Шаг 1 — Расчет дневной доходности
Сначала мы рассчитаем таблицу дневной доходности на основе дневных рядов обменных курсов доллара США к евро. Каждый доход рассчитывается с применением LN (P1 / P0) , где LN — функция натурального логарифма в EXCEL, P1 — новый обменный курс, P0 — старый обменный курс. Это примерно равно дневному процентному изменению цены базового обменного курса.
Ежедневная доходностьМы возьмем этот ряд доходностей и воспользуемся им для расчета гистограммы, подобной гистограмме выше.
г. Шаг 2. Настройте и запустите инструмент «Гистограмма анализа данных» EXCEL
Инструмент «Гистограмма» можно найти на вкладке «Анализ данных» в Excel. Если по какой-либо причине в вашей версии EXCEL вкладка анализа данных не отображается, для включения вкладки выполните следующие действия:
- Перейдите к параметрам EXCEL
- Выберите надстройки и
- Добавьте надстройку анализа данных.
Для создания гистограммы выберите серию дневной доходности, вычислив процентное изменение цен от одного дня к другому.Используйте эту возвращаемую серию в качестве входного диапазона.
Выберите новый слой рабочего листа, совокупный процент и вывод диаграммы (см. Ниже), чтобы увидеть графическое представление гистограммы, а также вспомогательную таблицу.
Настройка функции гистограммыКогда вы нажмете ОК, EXCEL создаст для вас новую вкладку и покажет гистограмму, которую вы видите ниже.
Сгенерированная гистограммаc. Шаг 3 — Интерпретация результатов гистограммы
Как специалист по рискам, мы сосредоточены на обратной стороне, которая на гистограмме ниже отмечена как -2.77%. Потенциал роста составляет около 1,99 +%.
и. Наихудший случай потери?
Итак, если я спрошу вас, что самое худшее, что может случиться, вы легко скажете мне, что мой худший сценарий, основанный на исторической доходности, как показано на гистограмме выше, — это потеря более -2,77% (крайний левый угол внизу ), если у меня длинная (купленная) позиция в евро, или убыток в размере 1,99%, если у меня короткая (проданная) позиция в евро по отношению к доллару США.
ii. Временной период? Шансы?
Следующие два вопроса должны быть: через какое время и с какой вероятностью?
Доходность рассчитывается на ежедневной основе, поэтому ответ на первый вопрос касается любого торгового дня.
Второй ответ требует некоторой работы. На графике выше примерно 300 дней (количество дней). В худшем случае ваша потеря случается раз в 300 дней. Вероятность того, что вы увидите убыток, превышающий это число, составляет 1/300 или 0,33%.
К счастью, в таблице выходных данных гистограммы EXCEL уже есть таблица с этими вероятностями и числами.
Гистограмма — вывод таблицы — коэффициентiii. Собираем
Если собрать, останется только файл.Вероятность 55%, что вы или я увидим в худшем случае убыток более -2,77% в любой конкретный торговый день, если вы купили евро, и вероятность 1,1%, что вы увидите убыток более 1,99%, если вы продали евро.
Поздравляю. Добавив период удержания (данный торговый день) и вероятность (0,55% / 1,1%), вы преобразовали свое простое утверждение о том, что может произойти в худшем случае, в оценку стоимости, подверженной риску.
Обычно стоимость под риском (VaR) выражается в долларовом эквиваленте. Однако, поскольку здесь у нас была только процентильная доходность для работы, мы выразили ее в процентах.
Концептуально подверженная риску стоимость представляет собой прогнозируемый уровень потерь, от которых торговый отдел должен защитить себя в экстремальных условиях. Он используется в качестве прокси для суммы капитала, необходимого для поддержки таких убытков.
Подход исторического моделирования VaR3.
Альтернативные методы оценки стоимости под рискомПодход, который мы только что использовали для расчета стоимости под риском, также известен как подход исторического моделирования VaR.
Вы также можете рассчитать стоимость, подверженную риску, используя метод ковариации дисперсии (VCV) или метод моделирования Монте-Карло.
Подход исторического моделирования VaR работает с фактическим распределением результатов (ряды цен и доходности), подход VCV предполагает, что доходность распределена нормально (он налагает нормальное распределение), в то время как метод моделирования Монте-Карло использует функцию генератора для первого смоделировать серию цен, а затем применить тот же процесс, который мы использовали выше для исторического моделирования.
а. Использование правильных моделей
Как и в случае со специалистами-практиками, по мере того, как мы решаем новые проблемы (иногда создавая другие, более трудные для решения проблемы), мы накапливаем перечень предубеждений и предубеждений.
Мне очень нравится моделирование методом Монте-Карло как инструмент для разделения структур и тестирования стратегий ценообразования и хеджирования. Однако я ненавижу это (моделирование методом Монте-Карло), когда дело касается моделирования рисков. Я понимаю, что подход исторического моделирования имеет много существенных ограничений. Но за прошедшие годы это единственный подход, который продемонстрировал некоторую стабильность. По словам Нассима Талеба, история не повторится, вы не пострадаете от последней худшей потери, и следующая большая волна, которая уничтожит вас, придет не там, где вы ее ожидаете.
Мое уважение к историческому моделированию возросло, когда мы начали моделировать стоимость под риском для кросс-валютных свопов. Две отдельные валюты, две отдельные процентные ставки, две отдельные временные структуры и около тысячи допущений между ними. Я смотрел на конечную цифру, которую наш симулятор Монте-Карло выдавал в изумлении, и задавался вопросом, как можно было бы полагаться на то, что буквально сшито вместе с помощью жевательной резинки и проволоки.
Хотя историческое моделирование имело свои проблемы, по крайней мере, оно уменьшило набор допущений, а использование набора исторических данных о ценах по валютным парам, курсам, временным структурам и рынкам значительно упростило объяснение трейдерам.Трейдеры понимают и уважают историю цен и цен. Они ставят под сомнение предположения. Модель, которая использует исходные цены, не ограниченные драйверами и предположениями для трейдера, бесконечно превосходит модель с большим количеством предположений, чем уравнений.
Дополнительные примеры и инструкции см. В следующих уроках:
Обучение преподаванию с использованием параметрических вычислений и моделирования Монте-Карло
% PDF-1.7 % 1 0 объект > / Metadata 2 0 R / Outlines 5 0 R / Pages 3 0 R / StructTreeRoot 6 0 R / Type / Catalog / Viewer Настройки >>> эндобдж 2 0 obj > поток application / pdf
Функция VAR.P — формула, примеры, как использовать VAR .P в Excel
Что такое функция VAR.P?
Функция VAR.P относится к категории Статистических функций Excel ФункцииСписок наиболее важных функций Excel для финансовых аналитиков. Эта шпаргалка охватывает 100 функций, которые критически важно знать аналитику Excel.Эта функция вернет дисперсию заданного набора значений. Он был представлен в версии MS Excel 2010 года.
Дисперсия — это статистическая мера, используемая для набора значений, чтобы определить, насколько значения отличаются от среднего значения.
Как финансовый аналитик Описание работы финансового аналитика Описание работы финансового аналитика, приведенное ниже, дает типичный пример всех навыков, образования и опыта, необходимых для работы аналитиком в банке, учреждении или корпорации.Выполняйте финансовое прогнозирование, отчетность и отслеживание операционных показателей, анализируйте финансовые данные, создавайте финансовые модели, функция VAR.P может быть полезна при вычислении отклонений в доходах. Менеджеры портфелей Менеджеры портфелей Менеджеры портфелей управляют инвестиционными портфелями, используя шестиэтапный процесс управления портфелем. Узнайте, что именно делает менеджер портфеля в этом руководстве. Управляющие портфелем — это профессионалы, которые управляют инвестиционными портфелями с целью достижения инвестиционных целей своих клиентов.часто используют эту функцию для измерения и отслеживания рисков своих портфелей.
Формула
= VAR.P (число1, [число2],…)
Функция VAR.P использует следующие аргументы:
- Number1 (обязательный аргумент) — это первый аргумент, соответствующий популяции.
- Число 2, .. (необязательный аргумент) — здесь числовые аргументы могут быть до 254 значений или массивов значений, которые предоставляют как минимум два значения функции.
При предоставлении аргументов мы должны помнить, что:
- VAR.P предполагает, что данные представляют всю генеральную совокупность. Если данные представляют собой образец, вычислите дисперсию с помощью VAR.S.
- VAR.P оценивает только числа в ссылках, игнорируя пустые ячейки, текст и логические значения, такие как ИСТИНА или ЛОЖЬ.
- Аргументы могут быть числами или именами, массивами или ссылками, содержащими числа.
- Аргументы могут быть жестко запрограммированными значениями вместо ссылок.
- Для оценки логических значений и / или текста используйте функцию ДИСПРА.
Как использовать функцию VAR.P в Excel?
В качестве функции рабочего листа VAR.P можно ввести как часть формулы в ячейку рабочего листа. Чтобы понять использование функции, рассмотрим пример:
Пример
Предположим, нам даны ежемесячные показатели продаж компании за последние три года, как показано ниже:
Для Для дисперсии данной совокупности используется формула:
Мы получаем следующие результаты:
В приведенном выше примере мы использовали аргументы для VAR.Функция P в качестве входных данных в виде трех диапазонов ячеек. Однако мы также можем вводить цифры напрямую, либо как отдельные числа, либо как числовые массивы.
Несколько вещей, которые следует помнить о функции VAR.P
- # DIV / 0! ошибка — возникает, если мы не предоставили числовые значения в качестве аргументов.
- # ЗНАЧЕНИЕ! error — возникает, когда любое из значений, предоставленных непосредственно этой функции, является текстовым значением, которое нельзя интерпретировать как числа.
- Функция VAR.P используется при вычислении дисперсии генеральной совокупности.Если ваши данные представляют собой всего лишь образец генеральной совокупности, вам следует использовать функцию ДИСПР.
Щелкните здесь, чтобы загрузить образец файла Excel
Дополнительные ресурсы
Спасибо за то, что прочитали руководство CFI по функции Excel VAR.P. Потратив время на изучение и освоение этих функций, вы значительно ускорите свое финансовое моделирование. Чтобы узнать больше, ознакомьтесь с этими дополнительными ресурсами CFI:
- Функции Excel для FinanceExcel for Finance Это руководство по Excel для финансов научит 10 основных формул и функций, которые вы должны знать, чтобы стать отличным финансовым аналитиком в Excel.В этом руководстве есть примеры, скриншоты и пошаговые инструкции. В конце скачайте бесплатный шаблон Excel, который включает в себя все финансовые функции, описанные в учебнике.
- Расширенный курс формул Excel
- Расширенные формулы Excel, которые вы должны знать Расширенные формулы Excel, которые необходимо знать Эти расширенные формулы Excel очень важно знать и потребуют вашего финансового анализа навыки на новый уровень. Расширенные функции Excel
- Ярлыки Excel для ПК и MacExcel Ярлыки ПК MacExcel Ярлыки — Список наиболее важных и распространенных ярлыков MS Excel для пользователей ПК и Mac, специалистов в области финансов и бухгалтерского учета.Сочетания клавиш ускоряют ваши навыки моделирования и экономят время.

 В результате возникает занижение оценки VAR по сонаправленной с трендом позиции (в приведенном примере — длинной). Для рынков с выраженным трендом модель может быть скорректирована по аналогии с моделями имитационного моделирования, либо исключением тренда из исходных данных.
В результате возникает занижение оценки VAR по сонаправленной с трендом позиции (в приведенном примере — длинной). Для рынков с выраженным трендом модель может быть скорректирована по аналогии с моделями имитационного моделирования, либо исключением тренда из исходных данных. Числовые аргументы 2—255, соответствующие выборке из генеральной совокупности.
Числовые аргументы 2—255, соответствующие выборке из генеральной совокупности.
