Какие подходы выделяют при расчете var – стоимость риска формула
ГЛАВА 6 СТОИМОСТЬ ПОД РИСКОМ (Value at Risk)
Предыдущая11121314151617181920212223242526Следующая
Общие замечания
Показатель VaR(Value at Risk) появился в 90-е годы прошлого века. Определяет стоимость портфеля финансовых активов, которой рискует инвестор. Появление VaR связано с тем, что во многих случаях дисперсия не может служить хорошим показателем, измеряющим риск портфеля активов.
VaR- показатель риска, показывающий, какой максимальный ущерб может понести актив или портфель активов инвестора в течение определенного периода времени с заданной доверительной вероятностью.
Предполагается, что в период времени, для которого производится оценка, изменение в портфеле активов не происходит. Наиболее распространенный период, на который рассчитывается VaR – один день. Чем больше период, на который рассчитывается VaR, тем большее количество наблюдений необходимо. Так, для объективной оценки однодневного VaR, достаточно 250 однодневных наблюдений, для оценки десятидневного VaR, с непересекающимися периодами в 10 дней потребуются данные почти за семь лет.
Кроме технических трудностей получить данные за большой период времени, следует пониметь, что эти данные будут недостаточно представительными из-за динамичного развития рынков.
Какой риск измеряет VaR. Согласно методике расчета, VaR оценивает возможность потерь, вызванных рыночным риском, который проявится в изменении цены (и соответственно доходности) финансовых инструментов. Предполагается, что цена способна отразить в себе проявление большинства рисконесущих факторов. Поэтому инвесторы склонны смотреть на VaR как на меру всех рисков, связанных с финансовыми инструментами. В некоторых работах, указывается, что реальный размер убытков может оказаться большим, чем это оценивает VaR, если учитывать политические риски, риски ликвидности, регуляторные риски, которым подвержены финансовые активы.
Второе замечание связано с трактовкой прибыли и убытков в VaR, который рассматривается априори как отрицательный фактор. Так, определяя ушерб с 99% вероятностью, мы исходим из того, что ожидаемая стоимость портфеля равна не средней, а практически максимально возможной.
Временной характер VaR. В большинстве своих применений VaR вычисляется на короткие промежутки времени – один день, неделя, месяц. Чем короче оцениваемый период, тем точнее оценки VaR. Поэтому, этот показатель, как правило, используется компаниями при оперативном управлении рыночными рисками.
На Кубке мира по футболу-2018 впервые используют технологию VAR: что это такое?
В отличие от других мер риска, таких как стандартное отклонение или 
, которые дают представление о некотором усредненном риске, VaR дает представления о потерях в конкретный период
Ограничения VaR.Полагают, что использование методов VaR может привести к ошибочным результатам, которые будут вызваны следующими обстоятельствами:
· Распределение доходностей. Для каждого показателя VaR предполагается наличие определенного распределения доходностей;
· История – не очень хорошая база для реальных прогнозов. Во всех прогнозах VaR в той или иной степени используются исторические данные. Если период, за который взяты исторические данные был стабильным, VaR будет небольшим, если нестабильным, то – будет принимать большие значения. Однако, в рыночной экономике, отклонения, любые отклонения приводят к появлению механизмов, которые восстанавливают нарушенное равновесия. Тогда, достаточно ненадежной смотрится идея строить суждения о будущей рисках исходя из бывших отклонениях, учтенных экономикой.
· Нестационарные корреляции. Оценки VaR зависят от корреляционных связей источников риска. Корреляционные связи обычно основываются на исторических данных и являются волонтильными. Поскольку всякий раз , в расчетах, используется только одна корреляционная матрица, качество оценок зависят от того, насколько правильная матрица корреляций была использована.
Достоинства методологии VaR.Несмотря на известную критику, метод VaR успешно используется в практике многих финансовых институтов. Среди достоинств этого метода выделяют следующие:
· Использование портфельного подхода к рассмотрению структуры активов;
· Расчет ожидаемой прибыли определяется реальными рыночными ставками финансовых инструментов, а не базовыми рыночными ставками, имеющими аналитическую природу;
· За счет использования корреляционных матриц получается более надежная оценка активов и портфелей активов, чем при помощи стохастического моделирования;
Существуют две группы методик VaR: а) аналитическими или дисперсионно-ковариационными модели; б) непараметрические модели.
Различные модели VaR
Параметрическая модель VaR
Модель называется параметрической, если нам известна функция распределения и параметры распределения случайной величины. В параметрической модели VaR предполагается, что доходности финансовых активов следуют определенному закону распределения, как правило, нормальному. Используя исторические наблюдения, определяют среднее значения, дисперсии и ковариации доходностей финансовых активов. На их основе определяют VaR портфеля с заданным доверительным уровнем по следующей формуле:
где — стоимость портфеля;
– стандартное отклонение доходностей портфеля, соответствующее периоду времени, для которого рассчитывается VaR;
– количество стандартных отклонений, соответствующее заданному доверительному уровню α.
Выделяют понятия абсолютного и относительного VaR. Абсолютный VaR определяет размер максимально возможной суммы которую инвестор может потерять в течение определенного периода времени с заданной вероятностью. Относительный VaR в отличие от абсолютного определяется относительно ожидаемой доходности портфеля.
В случае, когда инвестору известны VaR активов, входящих в его портфель, VaR портфеля определяется по формуле:
где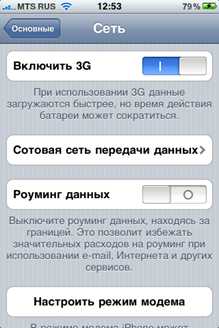 
— вектор-столбец и вектор-строка VaR активов портфеля;
– матрица корреляции активов портфеля
Если, при определении VaR портфеля, учитываются корреляции между активами, то речь идет о диверсифицированном VaR, если корреляции не учитываются, то говорят о недиверсифицированном VaR. Он представляет собой простую сумму индивидуальных VaR активов портфеля.
Поскольку корреляции могут изменяться со временем, то наряду с показателем диверсифицированный VaR, целесообразно определять недиверсифицированный VaR, который покажет максимальные потери для данного уровня доверительной вероятности при неустойчивых корреляциях или ошибках в их определении.
Предположение о нормальном распределении активов, входящих в портфель, позволяет переводить значение VaR из одного уровня доверительно вероятности в другой. Покажем на примере. Возьмем и . Выразим из первой формулы и подставим во вторую
Аналогичным образом можно пересчитать VaR для разных периодов времени.
Возьмем и . Выразим из первой формулы и подставим во вторую
Поскольку VaR определяется на основе статистических данных за определенный период времени, существует возможность получения оценок VaR, не соответствующих генеральной совокупности. В связи с этим, существует реальная необходимость оценки доверительного интервала для стандартного отклонения доходности портфеля активов.
Нижнюю ( ) и верхнюю( ) границы доверительного интервала можно определить и следующих формул:
где — нижняя и верхняя граница доверительного интервала стандартного отклонения доходностей инвестиционного портфеля
В случае, когда убытки могут превысить значение VaR инвестору необходимо знать, какие размер убытков он должен ожидать. В этом случае, используют следующее соотношение:
где — VaR активов портфеля при заданной доверительной вероятности γ;
– средние ожидаемые потери при условии, что фактические убытки X, окажутся больше чем .
Противоположным понятием, по отношению к VaR, является понятие EaR(Earnings at Risk), который показывает, какой максимальный доход может принести владение определенным портфелем финансовых активов в течение определенного периода времени с заданной доверительной вероятностью.
При выборе портфеля можно опираться на соотношение EaR к VaR. Чем больше это соотношение при определенном уровне доверительной вероятности, тем предпочтительнее портфель.
Предыдущая11121314151617181920212223242526Следующая
steptosleep.ru
Alexey Boyarskiy’s Blog: ПРОЦЕСС РАСЧЕТА VALUE-AT-RISK ОБЛИГАЦИЙ
Процедура расчета Value-at-Risk (VaR) по облигациям процесс довольно не простой, особенно если подходить к этому вопросу комплексно, как например расчёт стоимости под риском портфеля облигаций в целом.
Оценку степени риска портфеля облигаций целесообразней проводить посредством расчета показателя процентного риска DV01, но порой, для расчета совокупного показателя риска диверсифицированного портфеля активов, возникает потребность в использовании универсальной её величины, как для долевых финансовых инструментов (акций), так и для долговых (облигаций). В этом случае как раз и прибегают к расчету VaR по облигациям.
Ниже представлен максимально упрощенный комплексный вариант-пример процедуры расчета Value-at-Risk по рублевым облигациям, торгуемым на Московской бирже в среде Excel*:
Схема процесса расчета стоимости под риском (VaR) по облигациям
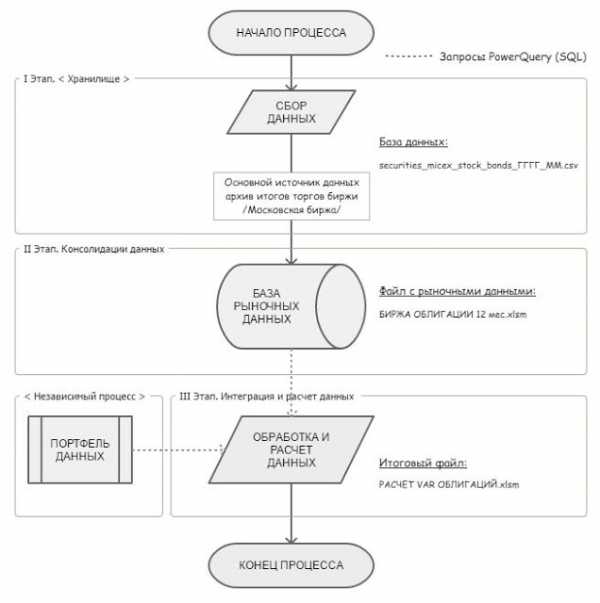
На первом этапе (см. на схеме <СБОР ДАННЫХ>) требуются рыночные данные, на базе которых будет происходить анализ и непосредственно расчет данных.
В качестве источника рыночных данных, использованы месячные данные, формируемые Московской Биржей по итогам ежедневных торгов. Информация, увы, доступна только на платной основе (по крайне мере, о наличии бесплатных альтернативных вариантов — неизвестно). Для расчета целесообразно использовать данные минимум за 12 месяцев.На следующем этапе <БАЗА РЫНОЧНЫХ ДАННЫХ> происходит процедура автоматического объединения, консолидации месячных данных за последний год.
Третий этап ОБРАБОТКА И РАСЧЕТ ДАННЫХ> — итоговый, здесь осуществляется точечная выгрузка рыночных данных и непосредственно сам расчет заявленного показателя Value-at-Risk по облигациям.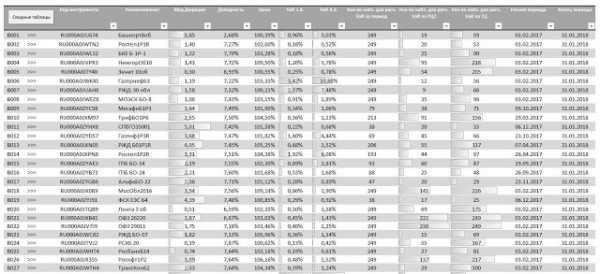
Представленный на схеме независимый процесс <ПОРТФЕЛЬ ДАННЫХ> это возможный к использованию вспомогательный элемент автоматической подгрузки данных о конкретном портфеле облигаций (в представленном ниже примере для скачивания этот процесс не поддерживается, но при желании не составит большого труда организовать автоматическую его подкачку).
Скачать приложения Вы можете здесь:
Приложение «Расчет VaR по облигациям».
Скачать
Краткая процедура к использованию*:
2. Разархивированные месячные данные поместить в папку:
…\РАСЧЁТ VAR ОБЛИГАЦИЙ\РАСЧЁТ VAR\А. БИРЖА КОТИРОВКИ\ОБЛИГАЦИИ\12 МЕС
3. Запустить файл <БИРЖА ОБЛИГАЦИИ 12 мес.xlsm> и выбрать на вкладке «Данные» — «Запросы и подключения«, далее здесь же нажать кнопку «Обновить все«. Дождаться завершения обновления данных, сохранить и закрыть файл.
4. Запустить файл <РАСЧЕТ VAR ОБЛИГАЦИЙ.xlsm>.
4.1. На листе «Сводный» файла ниже таблицы укажите дату расчета (последний рабочий день скаченных с биржи данных), перечисленные ниже параметры предлагается оставить без изменения (по умолчанию).
4.2. Выбрать на вкладке «Данные» — «Запросы и подключения» и далее здесь же нажать кнопку «Обновить все«.
4.3. Затем нажмите на кнопку «Сводные таблицы», расположенную в верхнем левом углу на листе «Сводный» файла.
Всё расчет готов!
Если есть потребность посчитать показатель риска непосредственно по собственному портфелю облигаций до шага 4.2. выполните следующие действия:
а) На листе «Service» файла в соответствующей таблице заполните данные о собственном портфеле.
б) Осуществите соответствующую частную выборку интересующих вас бумаг в соответствии с вашим портфелем облигаций следующим путем:
1) Выбрать на вкладке «Данные» — «Запросы и подключения«;
2) В таблице на листе «Сводный» файла в строке той или иной облигации, подлежащей замене, нажмите знак «>>>»;
3) Выберите соответственно имени листа, на который вы были переброшены, запрос в колонке справа и нажмите изменить как показано на рисунке ниже:
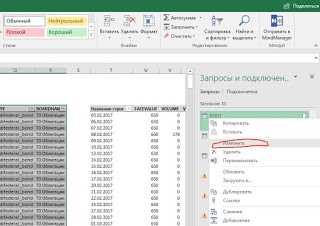
4) В открывшемся редакторе запросов в верхней строке укажите ISIN интересующей вас облигации, затем нажмите «Закрыть и загрузить».
Итак во всех запросах, бумаги которых вы хотите заменить. Чтобы убрать облигации, которые вам не интересны, в редакторе запроса просто удалите ISIN.Для корректной работы работы требуется Excel 2016 и выше.
abnsecurities.blogspot.com
VAR — техническая схема расчета
Одним из основных этапов оценки риска является подготовка данных — итоговая оценка риска во многом зависит от того, какой показатель и за какой период используется для расчета, причем для нестабильных развивающихся рынков вклад этого фактора в формирование конечной оценки риска становится первостепенным.
Здесь, в рамках общего подхода к статистическому анализу стоимости позиции, возможны два варианта:
1. Анализ текущей стоимости позиции.
2. Анализ динамики доходов и расходов.
Технически указанные варианты практически аналогичны, и выбор между ними должен осуществляться исходя из специфики объекта анализа. В рамках данной статьи, ориентированной на специфику российского рынка, за основу будет принят первый вариант.
Анализ текущий стоимости позиции, превалирующий в теоретической литературе и широко распространенный на практике, более универсален в реализации: для оценки риска необходима лишь регулярная (обычно – ежедневная) информация о рыночной стоимости текущей позиции. Фактически это означает, что основным риск-фактором, помимо фиксированной структуры позиции, становится рыночная история – динамика котировок по инструментам, составляющим позицию. Для статистической достоверности подобных расчетов обычно достаточно ежедневной статистики за 1-2 года.
Анализ доходов и расходов требует данных о результатах торговых операций за аналогичное количество торговых дней, причем для статистической корректности оценок каждый торговый день должен складываться из десятков и сотен сделок. Такой анализ возможен лишь для крупнейших операторов рынка, однако его несомненным преимуществом является принятие во внимание, помимо рыночных факторов, индивидуальной торговой стратегии. В этой связи последние годы именно этот вариант оценки VAR получает широкое распространение среди лидеров мирового финансового рынка.
При этом, в контексте агрегирования оценок отдельных рисков в общую оценку совокупного риска, разница между рассматриваемыми подходами достаточно существенна. Анализ текущей стоимости позиции в явном виде выделяет риск-факторы отдельных составляющих финансовых рисков — котировки ценных бумаг, валютные курсы, процентные ставки и т.п. — оценивая совокупный риск по схеме «снизу вверх», как сумму получаемых оценок отдельных рисков с корректировкой на взаимные корреляции и другие специфические факторы. Напротив, анализ доходов и расходов, дает общую оценку совокупного риска из которой далее «сверху вниз» выделяются отдельные составляющие (с непосредственной привязкой не столько к видам рисков, столько к видам операций и рынкам).
Итак, на первом этапе подготовки данных определяется исходный ряд показателей – ряд значений стоимости рассматриваемой (фиксированной) позиции для всех зафиксированных в историческом периоде состояний рынка. В зависимости от рыночных характеристик инструментов, составляющих позицию, специфики осуществляемых операций и целей анализа это может быть как непосредственно рыночная стоимость позиции, так и ее доходность, расчетные показатели цены (например, для опционов), а также ряд близких по экономическому смыслу рыночных показателей (сводных индексов и пр.).
Полученный временной ряд переводится в ряд относительных изменений: (см. Пример 1 в формате MSExcel).
Рассмотрение дневных изменений является теоретически классическим и наиболее распространенным вариантом, однако, в ряде практических приложений встречаются варианты внутридневного анализа (с шагом по сделкам, или по установленным промежуткам времени) или шага изменений в несколько дней.
Практически в любом случае возникают проблемы с потерей значимых промежуточных рыночных событий, либо, при использовании перекрывающихся интервалов, — технические сложности с повторным учетом отдельных изменений (поскольку фактически, как это показано на Рисунке 1, каждый сдвиг уровня показателей ряда участвует в формировании нескольких изменений), однако, с другой стороны, возникает дополнительный эффект учета последовательности изменений.
На основе указанных данных осуществляется непосредственно оценка VAR.
Основными, классическими и в равной степени актуальными на современном этапе методами оценки VAR считаются:
- метод исторического моделирования;
- метод параметрической оценки, наиболее распространенный в форме вариационно-ковариационной модели;
- метод имитационного моделирования, часто именуемый по основной применяемой в его рамках модели методом Монте-Карло.
Историческое моделирование
Оценка VAR методом исторического моделирования является технически предельно простой и одновременно достаточно наглядной. Вместе с тем предлагаемый подход полностью укладывается в описанную выше концепцию моделирования.
С другой стороны, в контексте портфельного VAR историческое моделирование является продолжением технического направления рыночного анализа, декларирующего тезис о концентрации в показателе цены (курса, котировки) полного объема рыночной информации, позволяющей на основе его динамики осуществлять всеобъемлющий анализ и прогнозирование конъюнктуры рынка, в т.ч. в части рисков.
Оценка VAR методом исторического моделирования в классическом варианте осуществляется по следующей схеме.
Полученный выше ряд относительных изменений упорядочивается, и очищается на часть наихудших значений, превышающую принятый доверительный уровень. Наихудшее из оставленных значений соответствует максимальной вероятной в рамках принятого доверительного уровня величине потерь, т.е. VAR – в соответствии с порядком расчета в форме относительного изменения стоимости (см. Пример 2 в формате MSExcel).
Необходимо отметить, что в стандартном и наиболее распространенном варианте отсекаются наименьшие изменения, что, строго говоря, корректно исключительно:
- либо для анализа длинных позиций, для которых риск проявляется только в снижении рыночной цены;
- либо для рынков с симметричным распределением изменений в обоих направлениях (по отношению к среднему значению).
Как видно из приведенного выше примера, на практике распределения вероятностей не всегда являются строго симметричными. Более того, для рынков с ярко выраженными долгосрочными трендами роль фактора асимметрии часто возрастает.
Полученная относительная оценка VAR приводится к абсолютному денежному эквиваленту в соответствии с использованными показателями.
Вариационно-ковариационная модель
Вариационно-ковариационная модель представляет собой альтернативный параметрический подход к оценке VAR.
В основе модели лежит предположение о соответствии фактического распределения случайной величины (рыночного показателя) определенной теоретической закономерности. Соответственно, на рассматриваемый рыночный показатель проектируются выводы, сделанные на основании расчетов по теоретическому распределению.
Методологически данный способ оценки VAR требует определенного математико-статистического аппарата, не в полной мере прозрачного для пользователей, которые могут не иметь специализированного образования. Вместе с тем, с технической точки зрения расчет является в высшей степени простым и обеспечивает оперативный пересчет показателей при минимальном компьютерном интерфейсе (система может быть в полном объеме реализована на основе стандартных электронных таблиц).
Наиболее распространенным моделирования вариантом является приближение рассматриваемой случайной величины нормальным распределением.
В целом, распределения случайных величин, близкие к нормальному, достаточно широко распространено в природе, что служит основой для большого количества моделей, применяемых во многих научных областях, и в т.ч. в экономике. Для широкого круга сложных процессов, формируемых взаимодействием большого количества случайных факторов, анализ на основе закономерностей, теоретически выведенных для нормального распределения, является статистически корректным. Это характерно, в частности, и для многих финансовых показателей, а именно цен финансовых инструментов, валютных курсов, котировок ценных бумаг и т.п. (см., например, Рисунок 2). Высокая степень соответствия стандартного, детально изученного математической статистикой нормального распределения и фиксируемых на практике распределений изменений котировок финансовых инструментов позволяет распространить теоретически обоснованные в отношении нормального распределения зависимости на динамику котировок и получить оценку оценка стоимости, подверженной риску — VAR — вариационно-ковариационным методом.
Общая схема оценки VAR вариационно-ковариационным методом может быть представлена следующим образом.
На первом этапе определяются параметры нормального распределения, наилучшим образом приближающего фактическое распределение рассматриваемого показателя — полученного выше ряда относительных изменений. Технически это может быть сделано различными способами, среди которых простейшими для применения могут быть признаны реализованные в рамках стандартного интерфейса электронных таблиц функции подбора параметров распределения.
Далее необходимо определить значения обратного нормального распределения в соответствии с полученными ранее параметрами и:
- установленным доверительным уровнем – для короткой позиции, риск по которой оценивается по положительным изменениям, либо
- обратным доверительным уровнем (т.е. 1 – доверительный уровень) – для длинной позиции и, соответственно, отрицательных изменений (см. Пример 3 в формате MSExcel).
При этом практически указанные варианты идентичны. В рамках рассматриваемого метода, в соответствии с техническими ограничениями применяемого статистического инструментария, не предусмотрена асимметрия распределений – расхождение между положительными и отрицательными изменениями составит удвоенное среднее значение распределения (т.е. будет соответствовать статистически выделяемому линейному тренду). Таким образом, при построении модели предполагается, что в рамках сложившейся долгосрочной рыночной конъюнктуры разнонаправленные движения при одинаковом отклонении от математического ожидания равновероятны. Для инструментов, в отношении которых такое предположение не соответствует фактической динамике, применение вариационно-ковариационных оценок в чистом виде (без дополнительных корректировок) не корректно.
Описанная процедура относится к стандартному инструментарию математической статистики. По сути, это соответствует принятию рассчитанного исходя из общих свойств нормально распределенных случайных величин соотношения стандартного отклонения, математического ожидания и наихудшего значения, получаемого с установленной вероятностью.
Полученное значение — относительная оценка VAR — приводится к абсолютному денежному эквиваленту в соответствии с формой исходного статистического ряда.
Необходимо отметить, что представленный выше алгоритм соответствует оценке VAR для 1 инструмента. Для составных портфелей расчет осуществляется по аналогичной схеме, но с использованием несколько более сложного матричного математико-статистического аппарата, детализированное рассмотрение которого не представляется целесообразным в рамках данной статьи. Кроме того, технический учет исторических корреляций означает, с точки зрения экономического содержания модели, предположение о сохранении имевших место разнонаправленных движений инструментов, что в ряде случаев может привести к занижению оценки риска.
Вместе с тем, для простых портфелей с несущественной внутренней корреляцией в качестве объекта рассмотрения может быть принят синтетический (искусственно составленный) инструмент.
Имитационное моделирование
В рамках развития моделей оценки VAR качественно новым шагом стало применение имитационного моделирования по методу Монте-Карло, в соответствии с наименованием которого обычно именуется данная оценка VAR. Принципиальное отличие VAR Монте-Карло от оценок исторического и вариационно-ковариационного моделирования является та особенность, что объектом моделирования выступает не только величина потерь, но и стоимость самого инструмента. В рамках данного метода потери определяются не по отношению к текущей стоимости инструмента, но по отношению к ее будущему наиболее вероятному значению, что с формальной точки зрения существенно более корректно.
Имитационное моделирование достаточно мало формализовано и не имеет жестких формальных ограничений. В основу модели может быть положено любое, в т.ч. комбинированное, распределение случайных величин или другая функциональная зависимость. Указанная специфика, наряду с пошаговым характером моделирования, определяет гибкость и достаточно высокую универсальность данного метода. VAR Монте-Карло может быть рассчитан по портфелям любой сложности, содержащим как простые «прямые» инструменты, так и сложные производные, с определенными и опциональными платежами (т.е. предполагающие различные варианты реализации прав по инструменту). В рамках данного метода непосредственно моделирование VAR также может быть дополнено динамическими сценариями изменения риск-факторов и базовых портфелей.
В классическом варианте оценка VAR методом имитационного моделирования осуществляется следующим образом.
Исходным шагом является определение формы и параметров распределения (функциональной зависимости) для рассматриваемого ряда. Как было отмечено выше, в соответствии с широким распространением на финансовых рынках нормальным распределением случайных величин, в моделировании финансовых рисков доминирует аппроксимация изменений показателей на основе нормальных распределений. Вместе с тем технически инструментарий данной модели не содержит никаких ограничений в части вида распределения, допуская любые, в т.ч. комбинированные функции.
Далее осуществляется непосредственно моделирование ряда изменений, распределенного в соответствии с полученными параметрами (для чего при простых вариантах распределений может быть применен стандартный математико-статистический инструментарий).
В зависимости от конкретного подхода возможно моделирование:
- фиксированного количества точек (обычно, не менее 300), либо
- до стабилизации среднего значения результатов моделирования с установленной точностью (но не менее установленного количества точек).
По результатам моделирования определяется: - среднее ожидаемое изменение;
- наихудшее в рамках установленного доверительного уровня ожидаемое изменение по направлению, соответствующему анализируемой позиции;
- VAR-оценку риска как абсолютное значение разности указанных величин.
Вариант расчета для нормального распределения в формате MS Excel см. в Примере 4.
При этом моделирование может осуществляться как для отдельного инструмента, так и совместно для всех элементов портфеля. Моделирование также возможно как на 1 день, так и на более длительный (либо короткий) промежуток времени, в соответствии со специфическими целями анализа. В процесс моделирования могут также быть интегрированы сценарные элементы для учета опциональных инструментов, динамики портфелей и/или внешних рыночных факторов.
Необходимо отметить, что имитационное моделирование не дает однозначного результата – по итогам каждого расчета формируется индивидуальное значение. Естественно, при условии корректного построения модели разброс указанных значений ограничен. В зависимости от целей анализа могут варьироваться требования к точности расчета, однако для технической реализации высокоточной модели может потребоваться технически сложный инструментарий.
Несмотря на определенную случайную составляющую результатов имитационного моделирования, в целом, при условии корректности расчета, они соответствуют оценкам, получаемым с помощью других методов, с возможными отклонениями, определяемыми свойствами конкретных моделей.
| Комментарий к результатам моделирования по 3 рассмотренным методам |
| Результаты расчета VAR на примере фондового индекса РТС с использованием методов исторического, параметрического и имитационного моделирования приведены в Примере 5. При условии корректности построения моделей значения, полученные различными методами, в целом должны быть согласованы (как это видно из приведенного примера), однако они не должны в точности совпадать. Вместе с тем необходимо отметить следующие моменты, частично упоминавшиеся выше по тексту:
|
www.riskinfo.ru
сравнение вариационно-ковариационного подхода с историческим / Блог им. foxerfx / Traders’ Club
Для начала напомним, что измеряет value at risk (VaR):показатель VaR говорит что на горизонте Т дней убытки не превысят Х денежных единиц с вероятностью Р.
Так, например, если однодневный VaR для портфеля равен -23000 долларов при уровне доверительной вероятности равном 0.95, это означает, что с вероятностью 0.95 убытки за один день по портфелю не превысят величину -23000 долларов и соответственно с вероятностью 1 — 0.95 = 0.05 превысят -23000 долларов.
Далее посмотрим как можно посчитать VaR вариационно-ковариационным способом и как его можно посчитать с помощью исторических данных. Затем сравним оба подхода.
Для вариационно-ковариционного VaR формулка очень простая:
VaR = — P * k * sigma * sqrt(T/252)
где:
P — стоимость портфеля;
k — квантиль для нормально распределения. Например для уровня доверительной вероятности 0.95, k = 1.645. То есть по сути сколько сигм нам нужно взять чтобы получить желаемый уровень доверительной вероятности;
sigma — годовая волатильность или стандартное отклонение доходности нашего портфеля за год;
T — горизонт для которого оцениваем VaR в днях;
252 — предположение о количестве бизнес дней в году;
sqrt(T/252) — отвечает за скейлинг волатильности на нужный нам горизонт, так как в финансах предполагается, что волатильность пропорциональна корню из времени.
sigma портфеля можно легко посчитать следующим образом:
1. Оцениваем матрицу ковариаций C между однодневными доходностями активов в портфеле в некотором «окне», например, на последних 252 днях.
2. Вычисляем вектор весов активов в портфеле W, так что их сумма равна 1.
3. Считаем дисперсию портфеля как sigma^2 = W’ * C * W, где ‘ означает транспонирование. Извлекаем из дисперсии квадратный корень и получаем sigma портфеля.
4. Умножаем полученную sigma на sqrt(252) чтобы получить годовую волатильность нашего портфеля.
Попробуем проделать все вышеприведенное на простом примере в Ексель для 2 акций, одна из которых Интел (INTC), а вторая — Техас Инструментс (TXN):
Скачав дневки с finance.yahoo.com за последний год оценим ковариацию между их дневными доходностями: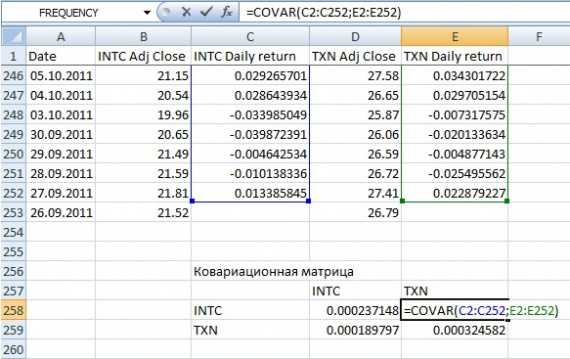
Следует обратить внимание, что матрица ковариаций является симметричной, а на главной диагонали стоят ковариации каждой акции с самой собой, что равно дисперсии доходности акции.
Теперь предположим что у нас куплено в лонг INTC на 250 000 USD и куплено в лонг ТXN на 750 000 USD. Тогда вектор весов будет (0.25;0.75).
Теперь вычислим сигму нашего портфеля:
Таким образом sigma = 0.26.
Теперь подставим все расчитанные величины в формулу выше для расчета VaR вариационно-ковариационным методом чтобы оценить однодневный VaR для портфеля из двух акций INTC и TXN стоимостью 1 000 000$ с доверительной вероятностью 0.95: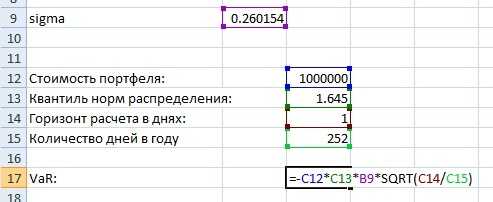
Таким образом VaR = -26958.6$. То есть с вероятностью 0.95 наши убытки по портфелю из двух акций за один день не превысят 26958.6$.
Теперь рассмотрим как можно посчитать однодневный исторический VaR для того же самого портфеля на 1 000 000$ из которых INTC в лонг на 250 000$ и TXN в лонг на 750 000$ для доверительной вероятности 0.95.
Общий подход к расчету исторического VaR следующий:
1. Определяем количество сценариев на истории по которым мы хотим посчитать VaR.
2. Для всех инструментов портфеля берем исторические треки цен по дням за одинаковый период равный количеству сценариев + 1.
3. Вычисляем дневные доходности каждого инструмента.
4. Для каждого дня на истории что представляет собой отдельный сценарий возможного поведения портфеля используя дневную доходность мы считаем дневную прибыль/убыток для каждого инструмента и затем суммарную прибыль/убыток по портфелю.
5. Получив вектор прибылей/убытков по портфелю для каждого сценария сортируем его от минимума до максимума.
6. Теперь необходимо определить так называемый номер критического сценария. Для этого необходимо заданную доверительную вероятность умножить на количество сценариев и округлить полученное значение до ближайшего целого.
7. Для получения VaR мы должны отсчитать от начала вектора который соответствует максимальной возможной прибыли количество сценариев равное номеру критического сценария полученного в пункте 6 и следующий сценарией за ним даст нам значение VaR.
Для нашего примера возьмем количество сценариев равным 250. Тогда расчет критического сценария будет следующим:
Получили номер критического сценарий равен 238.
Теперь построив вектор прибылей/убытков по портфелю для всех 250ти сценариев определим исторический VaR: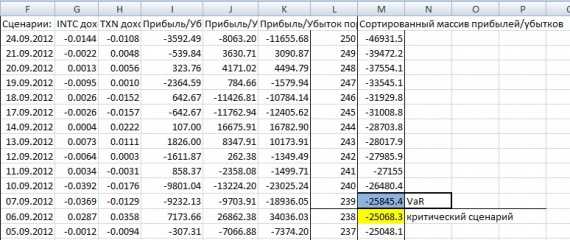
Таким образом однодневный исторический VaR для нашего примера равен -25845.4$.
Иногда озвученный подход расчета исторического VaR модифицируют за счет взвешивания исторических данных так, чтобы более старые данные имели меньший вес при расчете VaR чем более свежие данные.
Опять же выбранное количество сценариев для расчета определяет окно в котором будет оцениваться VaR и если это окно содержит в себе некоторые экстремальные события на рынке, то это будет учтено в полученной оценке VaR. То есть риск аналист может специально выбрать окно таким, чтобы захватить например период высокой волатильности на рынке и оценить VaR для него.
Если инструменты портфеля в разных валютах тогда необходимо определиться с базовой валютой портфеля и используя исторические треки курсов валют также учитывать прибыль/убыток от изменения валютного курса при расчете прибылей/убытков по каждому из инструментов портфеля для каждого сценария.
Сравнив вариационно-ковариационный VaR равный -26958.6$ и исторический VaR равный -25845.4$ увидим, что исторический VaR оценивает возможные убытки по портфелю меньше чем вариационно-ковариационный. Обычно получается наоборот. При большом количестве сценариев расчета исторического VaR его оценка убытков получается выше чем оценка полученная вариационно-ковариационным методом за счет учета реального распределения на рынке и наличия толстых хвостов в нем.
Сравнение двух подходов приводит с следующим плюсам/минусам для каждого из них.
Вариационно-ковариационный подход к расчету VaR:
Минусы:
1. Используемое предположение о нормальном законе распределения доходностей инструментов.
2. При расчет VaR на больше чем один день предполагается что матрица ковариаций постоянна.
3. Невозможно использовать для расчета VaR для опционов и инструментов с чертами опционов.
Плюсы:
1. Быстрый расчет, не требует больших вычислительных ресурсов.
2. Если в портфеле только линейные инструменты вроде акций, фьючерсов, валют может быть использован для расчета VaR.
3. Ковариационная матрица может быть получена от вендора чтобы не париться с расчетом самому.
Исторический подход к расчету VaR:
Плюсы:
1. Используется реальное распределение доходностей на рынке с реальными толстыми хвостами.
2. Матрица ковариаций не рассчитывается.
Минусы:
1. Трудности при расчете VaR для опционов так как опционные треки короткие и также проблемы с хранением большого количества опционных треков.
2. Инфраструктурные затраты предполагают, что должна быть БД где будут хранится и обновляться исторические треки цен для торгуемых инструментов.
В атаче к посту ексельчик который содержит все вычисления для приведенных примеров.
blog.quantquant.com
Все дело в рисках — ExpertOnline.kz
На цену акции влияет множество рыночных и макроэкономических факторов, настрой участников рынка, а также ситуация с ликвидностью. Даже самая хорошая бумага может упасть в стоимости из-за того, что, к примеру, крупным держателям акций будут нужны деньги и они начнут их продавать.
Риск падения стоимости инструмента принято называть ценовым. Ценовому риску подвержены акции, индексы, товары (commodity, металлы, зерно и т.п.), контракты на разницу и прочие производные финансовые инструменты, привязанные к одному из вышеуказанных активов.
В данной статье мы рассмотрим такие способы оценки ценового риска, как максимальное падение стоимости инструмента; волатильность; односторонняя волатильность; коэффициент Шарпа; Value at Risk.
Влияние рынка
Для примера рассмотрим две ценные бумаги: GDR (депозитарная расписка) Казкоммерцбанка (ККБ) и GDR Народного банка. На графике показаны цены на данные инструменты за последний год (глубина периода).
Анализируя динамику цен, можно сделать определенные выводы о потенциальных рисках ценной бумаги. Важный способ оценить риски – сравнить максимальное падение и максимальный рост стоимости акций за интересующий нас период. К примеру, возьмем один месяц, подразумевая, что инвестор планирует получить прибыль и продать бумаги в течение месяца со дня покупки. Для анализа показателя максимального роста делается предположение, что инвестор купил бумаги на самом «дне» (при минимально возможной стоимости) и в течение месяца они достигли пика. Аналогично для анализа показателя максимального роста делается предположение, что инвестор купил бумаги на самом пике, и в течение месяца они опустились до «дна». Формализованно наши расчетные величины будут выглядеть следующим образом:
- максимальный рост оценивается по формуле: (max-min)/min;
- максимальное падение рассчитывается по формуле: (min-max)/max.
Если проанализировать динамику цен GDR Казкома и Халыка, то получаются расчетные параметры, приведенные в графике 1.
Изменчивые цены
Следующий показатель оценки риска, который важен инвестору, это волатильность инструмента. Волатильность, или изменчивость, происходит от английского слова Volatility. Волатильность характеризует изменчивость финансового показателя во времени. В оценке рисков она показывает, насколько цена инструмента может меняться за определенный период времени.
Волатильность может выражаться в абсолютном или относительном от начальной стоимости значении. В математическом изложении волатильность представляет собой показатель выборочного стандартного отклонения. Расчет данного показателя не представляет сложности даже с помощью использования Excel. В данном приложении имеется функция «СТАНДОТКЛОН()», куда задаются соответствующие параметры.
Существуют различные способы использования волатильности.
Историческая волатильность показывает стандартное отклонение цены акции за определенный промежуток времени в прошлом. Ее значения нужны инвестору для того, чтобы видеть не только направление движения рынка, но и скорость, с которой меняются цены, чтобы вовремя понять, когда колебания стоимости достигнут критических для инвестора уровней.
В примере ниже мы рассчитываем дневную и месячную волатильность инструментов.
Волатильность акций Народного банка ниже. Это значит, что акции банка за этот период были менее подвержены ценовым колебаниям, следовательно, более предсказуемыми для инвестора инструментами.
Односторонняя волатильность является аналогом простой волатильности, но учитывает исключительно негативные изменения стоимости финансового инструмента. Так как инвестор хочет оценить именно риск, а движение бумаги вверх может оказать серьезное влияние на волатильность, то в целях оценки неблагоприятного движения имеет смысл исключить все положительные изменения стоимости акции из анализа и расчет вести только по негативным изменениям стоимости инструмента, которые могут повлечь за собой убыток для инвестора.
Риск-доходность
Следующая мера риска – коэффициент Шарпа. Он показывает, сколько доходности сверх безрисковой ставки приносит данный инструмент на единицу риска. Безрисковой ставкой доходности на нашем рынке обладают ноты Национального банка и облигации Министерства финансов Республики Казахстан в тенге.
Если финансовый инструмент показал доходность 12% со стандартным отклонением равным 6, а безрисковая ставка по нотам НБРК равна 4%, то коэффициент Шарпа будет равен (12–4)/6 = 1,3. Таким образом, за каждую единицу риска были получены 1,3 единицы доходности сверх безрисковой доходности.
Коэффициент Шарпа используется для сравнения доходности различных инструментов.
Понять движение цен
Следующим методом оценки риска является VaR – Value at Risk, который переводится с английского как стоимость под риском. Это выраженная в денежных единицах оценка величины, которую не должны превысить ожидаемые в течение заданного (конкретного) периода времени потери. Вычисление VaR позволяет инвестору утверждать, что его потери не превысят определенную сумму средств на определенный процент и с определенной вероятностью.
Концепция VaR основывается на прогнозировании убытков за заданный период времени с заданной вероятностью. Расчет VaR опирается на исторические цены инструмента и помогает сделать прогноз по поведению цены в будущем. Основным допущением модели является то, что ценовая история повторяется, и будущие изменения цены могут быть объяснены прошлыми изменениями. Конечно, это не всегда так, но в целом модель VaR может достаточно адекватно оценить риски по финансовым инструментам.
Существует три базовых метода оценки VaR: исторический, параметрический (его еще называют Variance-Covariance VaR) и Монте-Карло. В данной статье мы разберем исторический VaR, являющийся для начинающего инвестора наиболее легко реализуемым и понятным. При расчете VaR необходимо выбрать уровень доверия или вероятности события. Меняя уровень доверия, можно выбирать точность модели. Исторический дневной VaR с уровнем доверия в 95% показывает максимально возможный размер убытка за один день с вероятностью в 95%. Это означает, что в девяноста пяти днях из ста фактический убыток не превысит расчетного значения VaR. Например, если у вас есть 100-процентные изменения с шагом 1%, начиная от минус 1% и заканчивая минус 100% (полная потеря стоимости до нуля), то VaR с уровнем доверия в 95% будет равен именно 95%, то есть выбирается 95 по величине изменения. VaR при уровне доверия 100% будет равен 100%, в то время как VaR с уровнем доверия 50%, соответственно, будет равен 50%. Для расчета VaR в приложении Excel сначала необходимо посчитать процентные изменения стоимости финансового инструмента (для примера возьмем акции). Если инвестора интересует VaR на один день, то процентные изменения стоимости необходимо считать на базе «дня ко дню». Если необходимо рассчитать VaR на месяц, то считаются процентные изменения на базе «месяц к месяцу», то есть 1 октября сравнивается с 1 сентября, 2 октября со 2 сентября и так далее. Оптимальной глубиной периода (интервалом времен), за который берется история, по которой проводится расчет, являются 252 торговых дня. Они соответствуют примерно календарному году. Выбор такого срока позволяет учитывать необходимые изменения в прошлом, но в то же время не уменьшает вес сегодняшнего дня. Расчет VaR в Excel реализуется с помощью функции «Персентиль» в русском офисе, и Percentile в английском. В соответствующих окошках функции необходимо указать процентные изменения цены акции за последние 252 рабочих дня и нужный уровень доверия. Давайте посчитаем дневной и месячный VaR по тем же инструментам. Расчеты проводились на 1 октября 2009 года.
При горизонте инвестирования 1 день стоимость под риском по акциям Народного банка ниже, чем по акциям Казкоммерцбанка, в то время как при горизонте инвестирования 1 месяц стоимость под риском по акциям Народного банка выше, чем по акциям Казкоммерцбанка. Также мы видим, что однодневные риски по портфелю, который на 50% инвестирован в акции Казкоммерцбанка и на 50% в акции Народного банка, ниже, чем индивидуальные риски по каждой бумаге. Это классический пример диверсификации, когда риски по портфелю снижаются из-за того, что инструменты порой имеют разную направленность движения, то есть бывают ситуации, когда акции Народного банка растут, в то время как акции Казкоммерцбанка падают, либо наоборот.
Для частного инвестора расчет рисков можно легко проводить в Excel, в то время как профессиональным участникам рынка ценных бумаг с серьезными объемами операций, с финансовыми инструментами требуется более серьезное автоматизированное решение, которое позволит вести расчет всех видов рисков в режиме онлайн (online) по сравнительно большому портфелю ценных бумаг.
Современные IТ-решения предлагают разнообразные варианты расчетных модулей, которые позволяют рассчитывать все виды рисков (включая ценовой риск тремя способами VaR) в режиме онлайн, вести мониторинг исполнения лимитов, выстраивать систему внутреннего контроля. В частности, требованиям Агентства финансового надзора в области автоматизации расчетов риска удовлетворяют модули D-Risk, Risk Metrics и SunGard Ambit.
[inc pk=’169′ service=’table’][inc pk=’170′ service=’table’][inc pk=’171′ service=’table’][inc pk=’172′ service=’table’]expertonline.kz
Рассчет эффективности инвестиционного портфеля в Excell
Как и было обещано в предыдущей статье, в этой будет рассказано о том, как рассчитать основные показатели эффективности инвестиционного портфеля непосредственно в Excel http://utmagazine.ru/posts/5908-kak-rasschitat-effektivnost-portfelya-cennyh-bumag
Мы уже выяснили, что несмотря на казалось бы сложные термины и индикаторы, рассчитать эти индикаторы на самом деле не так уж и сложно. В случае с расчетами в Excel эти расчеты делать будет еще проще, так-как процесс в целом автоматизирован. Необходимо лишь грамотно расставить ячейки и сделать ссылки на соответствующие ячейки. И поскольку с показателями доходности в целом все понятно, рассматриваться будут лишь расчеты индикаторов риска.
Так как в предыдущей статье уже были определения основным индикаторам риска, в данном случае, чтобы не перегружаться лишней информацией, речь будет идти лишь о самих расчетах. Обо всем по порядку.
На всякий случай повторим основные показатели риска: стандартное отклонение доходности портфеля и каждого актива в отдельности от доходности рынка; коэффициент Шарпа; коэффициент бета; коэффициент Трейнора; Альфа Дженсена; коэффициент Швагера; коэффициент Сортино; М-квадрат. По очереди теперь разберемся с расчетом каждого из этих индикаторов в Excel. Стоит наверное всех обнадежить – сделать это довольно просто, по крайней мере гораздо легче, чем может показаться на первый взгляд. Более того, в случае расчетов в Excel достаточно просто использовать соотвтетсвующие функции. Сразу оговоримся, что все цифры условные и взяты из предыдущей статьи.
Стандартное отклонение – самый простой из всех показателей для расчетов. Для его расчета необходима лишь доходность портфеля относительно рынка. Необходимо лишь в соответствующую ячейку вставить формулу «СТАНДОТКЛОН.В(…)» и выбрать соответствующий массив данных по доходности.
Коэффициент Шарпа – разница в доходности портфеля к безрисковому активу, деленная на стандартное отклонение портфеля. Формула рассчитывается просто: при доходности портфеля в 2% и полученному стандартному отклонению 0.5%, а также и доходности безрискового актива в 0.4%, необходимо от первой ячейки отнять вторую и все это разделить на третью.
Коэффициент бета – скорость изменения доходности портфеля по сравнению с доходностью рынка. Соответственно необходимо математически рассчитать насколько доходность рынка влияет на доходность портфеля. Формула используется лишь два показателя: ковариация портфеля и рынка (произведение сумм корелляции и стандартного отклонения портфеля и рынка) и дисперсия доходности рынка (рассчитывается как стандартное отклонение в квадрате).
Для начала рассчитаем коэффициент ковариации. При корелляции портфеля с рынком в 0.7, стандартного отклонения рынка 0.3% и стандартного отклонения портфеля 0.5%, получается ковариация 0.7*0.3%*0.5%=0.0000105. Для расчета дисперсии рынка достаточно стандартное отклонение возвести в квадрат: 0.3%^2=0.000009. Отсюда находим бета-коэффициент 0.0000105/0.000009=1.16667.
Из полученных данных теперь рассчитаем коэффициент Трейнора – отношение премии за риск рынка и самого риска портфеля. Для его расчета требуется всего три показателя: общая доходность рынка, общая доходность портфеля и бета-коэффициент портфеля. При полученных выше показателях получается: (20%-15%)/1.16667=0.04285.
Альфа Дженсена – коэффициент, показывающий, насколько более эффективно активное управление портфелем по сравнению с пассивным. Для расчета необходимы 4 показателя: средняя доходность портфеля (2%), средняя доходность рынка (1.5%), доходность безрискового актива (0.4%) и коэффициент бета портфеля (1.16667). Чем больше значение данного коэффициента, тем более эффективно управляется портфель.
Коэффициент Швагера – отношение прибыли портфеля к средней максимальной просадке. Мы условно взяли данные за год при объеме портфеля в 500 тыс. долларов. Для расчета необходимо всего два показателя: среднегодовая доходность портфеля (500*0.2=100 тыс. долларов) и максимальная просадка (условно возьмем 5%: 500 *0.2=25 тыс. долларов). Далее делаем расчет по формуле.
Коэффициент Сортино, также как и показатель Шарпа, указывает на эффективность управления портфелем, но не ниже минимально допустимой доходности. Для начала рассчитаем минимально допустимую доходность. Как правило, за такой показатель берется доходность безрискового актива (0.4%). Таким образом, с учетом количества рабочих дней в году (условно 280) минимально допустимая дневная доходность составляет 0.4%/280=0,0014%.
Далее необходимо количество дней ниже минимально допустимой доходности (условно возьмем этот показатель 15). После этого можно рассчитать непосредственно сам коэффициент Сортино. Рассчитывается следующим образом: (2%-0.0014%)/15=0.0013.
Наконец, последний коэффициент – М-квадрат или просто М2. Данный индикатор указывает на то, насколько более высокую доходность показывает портфель, по сравнению с безрисковым активом. Для расчета требуются четыре показателя: средняя доходность портфеля (2%) и безрискового актива (0.0014%), стандартное отклонение доходностей портфеля (условно возьмем 1%) и стандартное отклонение доходности рынка (условно возьмем 0.5%).
Вот и все. Расчет всех эти коэффициентов в Excel оказался не таким уж и сложным, как и было обещано в начале статьи. После освоения этих двух материалов надеемся, что ключевые элементы портфельного анализа были успешно освоены.
utmagazine.ru
формула и расчет в Excel и интерпретация результатов
Коэффициент вариации в статистике применяется для сравнения разброса двух случайных величин с разными единицами измерения относительно ожидаемого значения. В итоге можно получить сопоставимые результаты. Показатель наглядно иллюстрирует однородность временного ряда.
Коэффициент вариации используется также инвесторами при портфельном анализе в качестве количественного показателя риска, связанного с вложением средств в определенные активы. Особенно эффективен в ситуации, когда у активов разная доходность и различный уровень риска. К примеру, у одного актива высокая ожидаемая доходность, а у другого – низкий уровень риска.
Как рассчитать коэффициент вариации в Excel
Коэффициент вариации представляет собой отношение среднеквадратического отклонения к среднему арифметическому. Для расчета в статистике используется следующая формула:
CV = σ / ǩ,
- CV – коэффициент вариации;
- σ – среднеквадратическое отклонение по выборке;
- ǩ – среднеарифметическое значение разброса значений.
Коэффициент вариации позволяет сравнить риск инвестирования и доходность двух и более портфелей активов. Причем последние могут существенно отличаться. То есть показатель увязывает риск и доходность. Позволяет оценить отношение между среднеквадратическим отклонением и ожидаемой доходностью в относительном выражении. Соответственно, сопоставить полученные результаты.
При принятии инвестиционного решения необходимо учитывать следующий момент: когда ожидаемая доходность актива близка к 0, коэффициент вариации может получиться большим. Причем показатель значительно меняется при незначительном изменении доходности.
В Excel не существует встроенной функции для расчета коэффициента вариации. Но можно найти частное от стандартного отклонения и среднего арифметического значения. Рассмотрим на примере.
Доходность двух ценных бумаг за предыдущие пять лет:
Наглядно это можно продемонстрировать на графике:
Обычно показатель выражается в процентах. Поэтому для ячеек с результатами установлен процентный формат.
Значение коэффициента для компании А – 33%, что свидетельствует об относительной однородности ряда. Формула расчета коэффициента вариации в Excel:
Сравните: для компании В коэффициент вариации составил 50%: ряд не является однородным, данные значительно разбросаны относительно среднего значения.
Интерпретация результатов
Прежде чем включить в инвестиционный портфель дополнительный актив, финансовый аналитик должен обосновать свое решение. Один из способов – расчет коэффициента вариации.
Ожидаемая доходность ценных бумаг составит:
Среднеквадратическое отклонение доходности для активов компании А и В составляет:
Ценные бумаги компании В имеют более высокую ожидаемую доходность. Они превышают ожидаемую доходность компании А в 1,14 раза. Но и инвестировать в активы предприятия В рискованнее. Риск выше в 1,7 раза. Как сопоставить акции с разной ожидаемой доходностью и различным уровнем риска?
Для сопоставления активов двух компаний рассчитан коэффициент вариации доходности. Показатель для предприятия В – 50%, для предприятия А – 33%. Риск инвестирования в ценные бумаги фирмы В выше в 1,54 раза (50% / 33%). Это означает, что акции компании А имеют лучшее соотношение риск / доходность. Следовательно, предпочтительнее вложить средства именно в них.
Таким образом, коэффициент вариации показывает уровень риска, что может оказаться полезным при включении нового актива в портфель. Показатель позволяет сопоставить ожидаемую доходность и риск. То есть величины с разными единицами измерения.
exceltable.com