Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
где
s2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Расчет дисперсии в Excel
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
D(A) = 0
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
D(AX) = А2 D(X)
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
D(A + X) = D(X)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
D(X+Y) = D(X) + D(Y)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
D(X-Y) = D(X) + D(Y)
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
=СТАНДОТКЛОН.В()/СРЗНАЧ()
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Поделиться в социальных сетях:
Показатели коэффициент вариации — Энциклопедия по экономике
Следующий показатель — коэффициент вариации, который характеризует величину риска на единицу ожидаемого результата и рассчитывается по формуле [c. 289]
289]Данный коэффициент показывает степень отклонения полученных значений. Он является относительной величиной, поэтому на его размер не оказывают влияния абсолютные значения изучаемого показателя. Коэффициент вариации может изменяться от 0 до 100%. Чем больше коэффициент, тем сильнее колеблемость и, следовательно, выше риск. Установлена следующая качественная оценка различных значений коэффициентов вариации [c.274]
Показатели и методы изучения колеблемости цен. Направления изучения вариации цен и их особенности. Проблемы расчета коэффициента вариации региональных цен. Показатели и методы исследования цикличности и сезонности цен. Вариация цен при наличии и изменении тенденции. [c.145]
Для общей характеристики структуры процесса, явления используют показатели размаха отклонений (максимального уровня от минимального), среднеквадратичного отклонения и коэффициента вариации. Простейшим показателем вариации служит размах колебаний А — разность максимальных и минимальных значений рассматриваемых показателей
[c. 20]
20]
Проведя детализацию показателей суточной производительности во времени, можно оценить стабильность работы установки, рассчитав показатель размаха А, среднеквадратичное отклонение а и коэффициент вариации v [c.46]
Предварительное исследование полученной выборки (дисперсионный анализ, определение закона распределения выборки и т. д.) позволяет в определенных пределах оценить значимость факторов по таким показателям, как размах варьирования, дисперсия и коэффициент вариации. Эти показатели характеризуют степень рассеивания наблюдаемых величин и свойства эмпирического наблюдения, что в определенной мере дополняет полученные ранее сведения о-характере влияния отобранных факторов. [c.16]
Высокая колеблемость наблюдается и по некоторым факторам. Так, коэффициент вариации V в % составляет для показателей [c.26]
Прямые показатели — коэффициент ритмичности, коэффициент вариации, удельный вес производства продукции за /-и период (декаду, месяц, квартал) в годовом объеме производства. [c.112]
[c.112]
Однородность информации оценивается в зависимости от относительного ее распределения около среднего уровня. Критериями служат среднеквадратическое отклонение и коэффициент вариации, определяемые по каждому факторному и результативному показателю. [c.75]
Таким образом, в приложении к финансовым операциям речь идет об оценке вариабельности ожидаемого дохода (доходности), а в качестве критериев оценки можно использовать такие статистические коэффициенты, как размах вариации, дисперсия, среднее квадратическое отклонение, называемое иногда стандартным, и коэффициент вариации. Дадим краткую характеристику этим показателям, имея ввиду, что в случае необходимости читатель может найти более подробную [c.83]
Все вышеприведенные показатели обладают одним общим недостатком — это абсолютные показатели, значение которых существенно зависит от абсолютных значений исходного признака ряда. Поэтому большее применение имеет коэффициент вариации, рассчитываемый по формуле
[c. 84]
84]
Для оценки выполнения плана по ритмичности используются прямые и косвенные показатели. Прямые показатели — коэффициент ритмичности, коэффициент вариации, коэффициент аритмичности, удельный вес производства продукции за каждую декаду (сутки) к месячному выпуску, удельный вес произведенной продукции за каждый месяц к квартальному выпуску, удельный вес выпущенной продукции за каждый квартал к годовому объему производства, удельный вес продукции, выпущенной в первую декаду отчетного месяца, к третьей декаде предыдущего месяца. [c.458]
Некоторое представление о колеблемости уровней процентных ставок в рассматриваемом периоде дает показатель размаха вариации. Однако эта абсолютная величина отражает колеблемость процентных ставок в пределах экстремальных значений признака. Более точными измерителями колеблемости являются дисперсия, среднее квадратическое отклонение и коэффициент вариации. [c.606]
Как видно из таблицы результатов расчета показателей вариации, колеблемость процентных ставок в 1996 г. сравнительно невысокая. Коэффициенты вариации отдельных видов процентных ставок изменяются в пределах от 13,32 до 28,51%.
[c.606]
сравнительно невысокая. Коэффициенты вариации отдельных видов процентных ставок изменяются в пределах от 13,32 до 28,51%.
[c.606]
С целью окончательного выбора формы тренда сопоставляют показатели вариации (дисперсию, среднее квадратическое отклонение и коэффициент вариации) эмпирических данных от- [c.613]
Значения показателей вариации, которые рассчитывают для уточнения формы тренда процентных ставок, могут оказаться достаточно высокими (например, коэффициент вариации составляет 35% и более), что свидетельствует о широкой амплитуде колебаний уровней фактических данных относительно выравненных. Это позволяет предположить, что динамика показателя складывалась под воздействием различных факторов, в том числе циклических, сезонных и случайных. [c.614]
При изучении изменчивости валютных курсов используют известный статистический инструментарий, исчисляя размах колебаний валютных курсов (R), дисперсию (52), стандартное (среднее) квадратическое отклонение ( ), коэффициент вариации (V).
Теоретическая статистика разрабатывает и изучает содержание, форму, методы расчета этих показателей в общем виде что такое средняя арифметическая величина, коэффициент вариации, уравнение тренда ряда динамики. Если же любой из этих показателей рассчитан для определенного объекта, признака, периода времени, то он становится уже конкретным показателем, например в главе 9 Статистическое изучение динамики показатели сезонных колебаний импорта КНР за 1992-1995 гг. — это уже конкретные статистические показатели экономики Китая. [c.46]
Рассмотренные направления проверки статистических гипотез охватывают лишь важнейшие из них. Процедура испытания статистических гипотез применяется для определения того, случайно или нет полученное значение коэффициента корреляции, коэффициента вариации и т.
Оба квадрата корреляционных отношений соответствуют по содержанию ранее рассмотренному коэффициенту детерминации (8.1) и (8.2) и интерпретируются как показатели доли вариации результативного признака, объясняемой за счет вариации группировочно-го, факторного признака (и, конечно, связанных с ним прочих факторов). В данном примере связь является тесной. Различие в том, что в эмпирическом корреляционном отношении связь признаков не абстрагирована от случайных влияний прочих факторов на вариацию у, не связанных с вариацией х. [c.255]
На основе качественного содержания понятия колеблемости строится и система ее показателей. Показателями силы колебаний уровней являются амплитуда отклонений уровней отдельных периодов или моментов от тренда (по модулю), среднее абсолютное отклонение уровней от тренда (по модулю), среднее квадратическое откло нение уровней от тренда.
Для оценки ритмичности поставок используются показатели среднеквадратичное отклонение фактического объема поставки по дням (декадам, месяцам) от среднего объема поставки коэффициент неравномерности поставок и коэффициент вариации [c.239]
Коэффициент вариации — величина относительная, поэтому на его размер не оказывают влияния абсолютные значения изучаемого показателя. С помощью коэффициента вариации можно сравнивать даже колеблемость признаков, вы- [c.41]
Коэффициент вариации показывает, что если отклонение расчетных показателей от фактических незначительно, то модель пригодна для планирования (прогнозирования) прибыли. [c.323]
Для оценки ритмичности поставок используются следующие показатели коэффициент ритмичности число аритмичности среднее квадратичное отклонение коэффициент неравномерности поставок коэффициент вариации. [c.357]
[c.357]
Т Определение. Коэффициент вариации — это особый показатель вариации, получаемый путем соотношения среднеквадратического отклонения и арифметической средней и выражаемый в процентах. А [c.46]
Следует отметить, что в отличие от других значений, представленных в данном разделе, коэффициент вариации не является овеществленной мерой разброса. Например, при рассмотрении заработной платы большинство показателей выражены в используемой денежной единице, скажем, в фунтах стерлингов. В противоположность этому коэффициент вариации не зависит от используемой единицы измерения. [c.46]
Так как коэффициент вариации для предложения В превышает аналогичный показатель для предложения А, мы можем сказать, что предложение В имеет более высокую степень риска. Можно поставить вопрос о целесообразности использования коэффициента вариации, ведь в нашем примере большая величина стандартного отклонения для предложения В уже свидетельствует о том, что оно более рискованное. Но сравнивать стандартное отклонение мы можем потому, что математические ожидания вероятностных распределений в нашем примере для обоих предложений были одинаковыми. А если бы они были разными В таком случае нам и нужен критерий относительной дисперсии, которым является коэффициент вариации. Математическое ожидание, стандартное отклонение и коэффициент вариации будут часто упоминаться в дальнейшем в этой главе.
[c.390]
Но сравнивать стандартное отклонение мы можем потому, что математические ожидания вероятностных распределений в нашем примере для обоих предложений были одинаковыми. А если бы они были разными В таком случае нам и нужен критерий относительной дисперсии, которым является коэффициент вариации. Математическое ожидание, стандартное отклонение и коэффициент вариации будут часто упоминаться в дальнейшем в этой главе.
[c.390]
В рассматриваемом примере коэффициент вариации составляет для проекта А = 7.03/30 = 0,24, для проекта В— 14,1/30 = 0,47. Чем выше коэффициент вариации, тем больше размер риска на единицу результата. Следовательно, проект б, имеющий более высокий коэффициент вариации, является более рисковым. В нашем примере решения о степени рисковости проектов можно было принять, не прибегая к расчету коэффициента вариации, а используя только показатели дисперсии или стандартного отклонения, так как математическое ожидание вероятностного распределения у обоих проектов одинаковое. Если же показатели математического ожидания вероятностного распределения различаются, то вывод об уровне риска проектов сделать на основе только показателей дисперсии и стандартного отклонения не представляется возможным. Проиллюстрируем это на примере двух проектов Си D (табл. 24.2). Рассматриваются также три сценария событий оптимистический (вероятность совершения которого составляет 75%), средний (50%) и пессимистический (25%).
[c.353]
Если же показатели математического ожидания вероятностного распределения различаются, то вывод об уровне риска проектов сделать на основе только показателей дисперсии и стандартного отклонения не представляется возможным. Проиллюстрируем это на примере двух проектов Си D (табл. 24.2). Рассматриваются также три сценария событий оптимистический (вероятность совершения которого составляет 75%), средний (50%) и пессимистический (25%).
[c.353]
В практике использования этого алгоритма размер возможных финансовых потерь выражается обычно абсолютной суммой, а вероятность возникновения инвестиционного риска — одним из коэффициентов измерения этой вероятности (коэффициентом вариации, бета-коэффициентом и др.) Соответственно уровень инвестиционного риска при его расчете по данному алгоритму будет выражен абсолютным показателем, что существенно снижает базу его сравнения при рассмотрении альтернативных вариантов. [c.150]
Общая структура процесса, явления характеризуется такими показателями, как максимальный и минимальный уровни, сред-неквадратическое отклонение и коэффициент вариации. Простейшим показателем вариации служит разность максимальных и минимальных значений рассматриваемых показателей (А). Однако этот показатель зависит от крайних значений и плохо характеризует изменения всех показателей в целом. Более полно степень колеблемости отражают среднеквадратическое отклонение а) и коэффициент вариации (V). Последний определяется отношением среднеквадратического отклонения к среднеарифметической величине и отражает стабильность, устойчивость процесса.
[c.141]
Простейшим показателем вариации служит разность максимальных и минимальных значений рассматриваемых показателей (А). Однако этот показатель зависит от крайних значений и плохо характеризует изменения всех показателей в целом. Более полно степень колеблемости отражают среднеквадратическое отклонение а) и коэффициент вариации (V). Последний определяется отношением среднеквадратического отклонения к среднеарифметической величине и отражает стабильность, устойчивость процесса.
[c.141]
Ввиду ограниченности количества данных при работе с двумя сопоставимыми отклоняющими компоновками необходимо установить точность и надежность средних значений показателей работы долот в обоих вариантах, а также выяснить, случайно или не случайно различие между ними. С этой целью полученные показатели работы долот в обоих вариантах бурения были обработаны методами математической статистики, описанной в главе IV. В результате этого данные, содержащие грубые ошибки, исключались из рассмотрения и не вошли в табл. 43. При этом было установлено, что средняя проходка на трехшарошечное долото Б-269С при бурении с кривыми переводниками с углом смещения осей резьб 2 и 2,5° составляет соответственно 30,7 и 24,4 м исправленное среднемвадратичбское отклонение 10,0 и 7,26 м коэффициент вариации 32,6 и 27,5% точность 2,70 и 1,67 м при вероятности 0,80.
[c.184]
43. При этом было установлено, что средняя проходка на трехшарошечное долото Б-269С при бурении с кривыми переводниками с углом смещения осей резьб 2 и 2,5° составляет соответственно 30,7 и 24,4 м исправленное среднемвадратичбское отклонение 10,0 и 7,26 м коэффициент вариации 32,6 и 27,5% точность 2,70 и 1,67 м при вероятности 0,80.
[c.184]
Уровень колеблемости показателей по НГДУ определяют с помощью среднеквадратичного отклонения, дисперсии и коэффициента вариации. Так, степень колеблемости уровня производительности труда по выборочной совокупности НГДУ по отношению к среднему показателю можно оценить с помощью среднеквадратичного отклонения в абсолютных единицах а и коэффициента вариации V в процентах по формулам [c.86]
Показатели Среднее значение Среднее квадрати-ческое отклонение Коэффициент вариации [c.26]
Данные, приведенные в табл. 15, показывают, что факторы, характеризующие уровень затрат подсистемы, имеют значительную колеблемость, которая обусловлена главным образом факторами природно-геологичес-кого характера. Вместе с этим некоторые факторы с высокой колеблемостью зависят от производственной деятельности коллектива и поэтому в большей степени, чем природные факторы, поддаются регулированию. k ним относятся такие показатели, как давление закачки на устье скважин (коэффициент вариации составляет 21,1%), удельный вес сточных вод в общем объеме закачки (коэффициент вариации равен 83 %). Высокая колеблемость этих факторов свидетельствует о больших возможностях снижения затрат на этом участке процесса добычи нефти. 38
[c.38]
Вместе с этим некоторые факторы с высокой колеблемостью зависят от производственной деятельности коллектива и поэтому в большей степени, чем природные факторы, поддаются регулированию. k ним относятся такие показатели, как давление закачки на устье скважин (коэффициент вариации составляет 21,1%), удельный вес сточных вод в общем объеме закачки (коэффициент вариации равен 83 %). Высокая колеблемость этих факторов свидетельствует о больших возможностях снижения затрат на этом участке процесса добычи нефти. 38
[c.38]
Показатели Среднее значение Среднее квадратичес-кое отклоне- Коэффициент вариации Коэффициент частной Г-критерий [c.40]
Показатель Среднее значение Среднеквадра-тическое отклонение Дисперсия Коэффициент вариации [c.83]
Для сравнения НГДУ лучшим показателем является коэффициент вариации (четвертая строка, табл. 27). Особенно отличается НГДУ по средним дебитам на отработанный скважино-месяц (в среднем 66,4%), временем эксплуатации (54%), фондоемкостью на одну
[c. 91]
91]
Для сравнения НГДУ лучшим показателем является коэффициент вариации (четвертая строка, табл. 31). Особенно отличается НГДУ по средним процентам обводненности нефти (в среднем 43,61%), времени эксплуатации (53,08%), фондоемкости на одну скважину (29,72%). Как следствие большой вариации факторов, наблюдается заметная вариация и уровня себестоимости добычи нефти и газа (18,4%). Силу связи между вариациями себестоимости добычи нефти и газа и факторов вскрывают частные коэффициенты корреляции. Наиболее сильно коррелируют с себестоимостью добычи нефти и газа обводненность нефти (0,52), средний дебит (0,38), время (0,14), а наиболее слабо — фондоемкость на одну скважину эксплуатационного фонда (0,1). [c.96]
Во-вторых, основными показателями оценки риска на рынке капитала являются дисперсия и среднее квадратическое отклонение. Распространенность и пригодность в сравнительном анализе этих статистик в данном случае объясняется тем обстоятельством, что базисным показателем при расчетах является доходность, т. е. относительный показатель, сопоставимый как в динамике, так и по различным видам активов. Поэтому независимо от анализируемых активов соответствующие им показатели доходности и дисперсии однопорядковы и нет острой необходимости применять в оценке коэффициент вариации.
[c.85]
е. относительный показатель, сопоставимый как в динамике, так и по различным видам активов. Поэтому независимо от анализируемых активов соответствующие им показатели доходности и дисперсии однопорядковы и нет острой необходимости применять в оценке коэффициент вариации.
[c.85]
Критерием однородности информации служит среднеквадра-тическое отклонение и коэффициент вариации, которые рассчитываются по каждому факторному и результативному показателю. [c.141]
Минимальный размах колебаний, дисперсии, среднего квадрати-ческого отклонения и коэффициента вариации имеет депозитные ставки, а максимальный — ставки по кредитам. Это свидетельствует о том, что наиболее стабильными в анализируемом периоде являлись депозитные ставки, так как они имели наименьшую изменчивость в течение года. Наименьшая устойчивость в 1996 г. была присуща ставкам по кредитам, так как именно этим процентным ставкам соответствуют самые высокие уровни показателей вариации. [c.607]
Коэффициент вариации КЙ представляет собой процентное отношение сред-неквадратического отклонения к среднеарифметическому значению отчетного показателя (например, прибыли)
[c. 322]
322]
При расчете относительных показателей вариации базой для сравнения служит средняя арифметическая. Эти показатели вычисляются как отношение размаха среднелинейного отклонения или средне-квадратического отклонения к средней арифметической. Чаще всего они выражаются в процентах или относительных величинах и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 0,3, или 30% (для распределений, близких к нормальному). Различают следующие относительные показатели вариации (У) [c.66]
Расчет показателей вариации в Excel
Оригинал http://statanaliz.info/index.php/excel/formuly/37-raschet-pokazatelej-variatsii-v-excel
Добрый день, уважаемые любители статистического анализа данных, а сегодня еще и программы Excel.
Проведение любого статанализа немыслимо без расчетов. И сегодня в рамках рубрики «Работаем в Excel» мы научимся рассчитывать показатели вариации. Теоретическая основа была рассмотрена ранее в ряде статей о вариации данных. Кстати, на этом указанная тема не закончилась, к выпуску планируются новые статьи – следите за рекламой! Однако сухая теория без инструментов реализации – вещь не сильно полезная. Поэтому по мере появления теоретических выкладок, я стараюсь не отставать с заметками о соответствующих расчетах в программе Excel.
Теоретическая основа была рассмотрена ранее в ряде статей о вариации данных. Кстати, на этом указанная тема не закончилась, к выпуску планируются новые статьи – следите за рекламой! Однако сухая теория без инструментов реализации – вещь не сильно полезная. Поэтому по мере появления теоретических выкладок, я стараюсь не отставать с заметками о соответствующих расчетах в программе Excel.
Сегодняшняя публикация будет посвящена расчету в Excel следующих показателей вариации:
— максимальное и минимальное значение
— среднее линейное отклонение
— дисперсия (по генеральной совокупности и по выборке)
— среднее квадратическое отклонение (по генеральной совокупности и по выборке)
— коэффициент вариации
Факт возможности расчета упомянутых показателей в Excel свидетельствует о практическом их использовании. И, несмотря на очевидность некоторых моментов, я постараюсь расписать все подробно.
Максимальное и минимальное значение
Начнем с формул максимума и минимума. Что такое максимальное и минимальное значение, уверен, знают почти все. Максимум – самое большое значение из анализируемого набора данных, минимум – самое маленькое (может быть и отрицательным числом). Это крайние значения в совокупности данных, обозначающие границы их вариации. Примеры реального использования каждый может придумать сам – их полно. Это и минимальные/максимальные цены на что-нибудь, и выбор наилучшего или наихудшего решения задачи, и всего, чего угодно. Минимум и максимум – весьма информативные показатели. Давайте теперь их рассчитаем в Excel.
Что такое максимальное и минимальное значение, уверен, знают почти все. Максимум – самое большое значение из анализируемого набора данных, минимум – самое маленькое (может быть и отрицательным числом). Это крайние значения в совокупности данных, обозначающие границы их вариации. Примеры реального использования каждый может придумать сам – их полно. Это и минимальные/максимальные цены на что-нибудь, и выбор наилучшего или наихудшего решения задачи, и всего, чего угодно. Минимум и максимум – весьма информативные показатели. Давайте теперь их рассчитаем в Excel.
Как нетрудно догадаться, делается сие элементарно – как два клика об асфальт. В Мастере функций следует выбрать: МАКС – для расчета максимального значения, МИН – для расчета минимального значения. Для облегчения поиска перечень всех функций можно отфильтровать по категории «Статистические».
Выбираем нужную формулу, в следующем окошке указываем диапазон данных (в котором ищется максимальное или минимальное значение) и жмем «ОК».
Функции МАКС и МИН достаточно часто используются, поэтому разработчики Экселя предусмотрительно добавили соответствующие кнопки в ленту. Они находятся там же, где суммаи среднее значение – в разворачивающемся списке.
В общем, для вызова функции максимума или минимума действий потребуется не больше, чем для расчета средней арифметической. Все архипросто.
Среднее линейное отклонение
Среднее линейное отклонение, напоминаю, представляет собой среднее из абсолютных (по модулю) отклонений от средней арифметической в анализируемой совокупности данных. Математическая формула имеет вид:
где
a – среднее линейное отклонение,
x – анализируемый показатель, с черточкой сверху – среднее значение показателя,
n – количество значений в анализируемой совокупности данных.
В Excel эта функция называется СРОТКЛ.
После выбора функции СРОТКЛ указываем диапазон данных, по которому должен произойти расчет. Нажимаем «ОК». Наслаждаемся результатом.
Нажимаем «ОК». Наслаждаемся результатом.
Дисперсия
Дисперсия — это средний квадрат отклонений, мера характеризующая разброс данных вокруг среднего значения. Математическая формула дисперсии по генеральной совокупности имеет вид:
где
D – дисперсия,
x – анализируемый показатель, с черточкой сверху – среднее значение показателя,
n – количество значений в анализируемой совокупности данных.
Excel также предлагает готовую функцию для расчета генеральной дисперсии ДИСП.Г.
При анализе выборочных данных, следует использовать выборочную дисперсию, так как генеральная оказывается смещенной в сторону занижения.
Математическая формула выборочной дисперсии имеет вид:
в Excel выборочная дисперсия рассчитывает через функцию ДИСП.В.
Выбираем в Мастере функций нужную дисперсию (генеральную или выборочную), указываем диапазон, жмем кнопку «ОК». Полученное значение может оказаться очень большим из-за предварительного возведения отклонений в квадрат, поэтому дисперсия сама по себе мало о чем говорит. Ее обычно используют для дальнейших расчетов.
Полученное значение может оказаться очень большим из-за предварительного возведения отклонений в квадрат, поэтому дисперсия сама по себе мало о чем говорит. Ее обычно используют для дальнейших расчетов.
Среднее квадратическое отклонение
Среднеквадратическое отклонение по генеральной совокупности – это корень из генеральной дисперсии.
Выборочное среднеквадратическое отклонение – это корень из выборочной дисперсии.
Для расчета можно извлечь корень из формул дисперсии, указанных чуть выше, но в Excel есть и готовые функции:
— Среднеквадратическое отклонение по генеральной совокупности СТАНДОТКЛОН.Г
— Среднеквадратическое отклонение по выборке СТАНДОТКЛОН.В.
С названием этого показателя может возникнуть путаница, т.к. часто можно встретить синоним «стандартное отклонение». Пугаться не нужно – смысл тот же.
Далее, как обычно, указываем нужный диапазон и нажимаем на «ОК». Среднее квадратическое отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными. Об этом ниже.
Об этом ниже.
Коэффициент вариации
Все показатели, рассмотренные выше, имеют привязку к масштабу исходных данных и не позволяют получить образное представление о вариации анализируемой совокупности. Для получения относительной меры разброса данных используют коэффициент вариации, который рассчитывается путем деления среднего квадартического отклонения на среднее арифметическое значение. Математическая формула такова:
В Экселе нет готовой функции для расчета коэффициента вариации, что не есть большая проблема. Расчет можно произвести простым делением стандартного отклонения на среднее значение. Для этого в строке формул пишем:
=СТАНДОТКЛОН.Г(диапазон)/СРЗНАЧ(диапазон)
В скобках должен быть указан диапазон данных. При необходимости используется среднее квадратическое отклонение по выборке (СТАНДОТКЛОН.В).
Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на ленте на закладке «Главная»:
Нужная кнопка находится на ленте на закладке «Главная»:
Изменить формат также можно, выбрав «Формат ячеек» из выпадающего списка после выделения нужной ячейки правой кнопкой мышки.
Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что если коэффициент вариации менее 33%, то совокупность данных является однородной, если более 33%, то – неоднородной. Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений. Полезное свойство.
В целом, с помощью Excel все, или почти все, статистические показатели рассчитываются очень просто. Если что-то непонятно, всегда можно воспользоваться окошком для поиска в Мастере функций. Ну, и Гугл в помощь.
Ну, и Гугл в помощь.
Легкой работы в Excel и до встречи на блоге statanaliz.info.
Оригинал и другие статьи http://statanaliz.info/index.php/excel/formuly/37-raschet-pokazatelej-variatsii-v-excel
Как найти коэффициент вариации
Как найти коэффициент вариации: Содержание :
- Что такое коэффициент вариации?
- Как найти коэффициент вариации
Посмотрите видео, чтобы узнать, как рассчитать коэффициент вариации:
Видео не видно? Кликните сюда.
Коэффициент вариации (CV) является мерой относительной изменчивости. Это отношение стандартного отклонения к среднему (среднему).Например, выражение «Стандартное отклонение составляет 15% от среднего» является CV.
Резюме особенно полезно, когда вы хотите сравнить результаты двух разных опросов или тестов, которые имеют разные меры или значения. Например, если вы сравниваете результаты двух тестов с разными механизмами оценки. Если образец A имеет CV 12%, а образец B имеет CV 25%, можно сказать, что образец B имеет большую вариацию по сравнению со своим средним значением.
Формула
Формула для коэффициента вариации :
Коэффициент вариации = (Стандартное отклонение / Среднее значение) * 100.
В символах: CV = (SD/x̄) * 100.
Умножение коэффициента на 100 является необязательным шагом для получения процента, а не десятичной дроби.
Коэффициент вариации Пример
Исследователь сравнивает два теста с несколькими вариантами ответов в разных условиях. В первом тесте проводится типичный тест с множественным выбором. Во втором тесте испытуемым случайным образом назначаются альтернативные варианты (то есть неправильные ответы). Результаты двух тестов:
Результаты двух тестов:
| Обычный тест | Рандомизированные ответы | |
| Среднее | 59.9 | 44,8 |
| SD | 10,2 | 12,7 |
Сравнить результаты двух тестов сложно. Сравнение стандартных отклонений на самом деле не работает, потому что означает, что тоже разные. Расчет по формуле CV=(SD/Mean)*100 помогает разобраться в данных:
| Обычный тест | Рандомизированные ответы | |
| Среднее | 59,9 | 44.8 |
| SD | 10,2 | 12,7 |
| Резюме | 17.03 | 28,35 |
Глядя на стандартные отклонения 10,2 и 12,7, можно подумать, что результаты тестов одинаковы. Однако, когда вы делаете поправку на разницу в средних значениях, результаты имеют большее значение:
Коэффициент вариации можно также использовать для сравнения изменчивости различных показателей. Например, вы можете сравнить показатели IQ с результатами теста когнитивных способностей Вудкока-Джонсона III.
Например, вы можете сравнить показатели IQ с результатами теста когнитивных способностей Вудкока-Джонсона III.
Примечание: Коэффициент вариации следует использовать только для сравнения положительных данных по шкале отношений. CV практически не имеет значения для измерений на интервальной шкале. Примеры интервальных шкал включают температуру в градусах Цельсия или Фаренгейта, тогда как шкала Кельвина представляет собой шкалу отношений, которая начинается с нуля и по определению не может принимать отрицательное значение (0 градусов Кельвина означает отсутствие тепла).
Нужна помощь с конкретным вопросом домашнего задания? Посетите нашу страницу обучения!
Используйте следующую формулу для расчета CV вручную для совокупности или выборки.
Эти формулы для коэффициента вариации дают проценты. Чтобы получить десятичную дробь, не умножайте на 100.
σ — стандартное отклонение для генеральной совокупности, такое же, как «s» для выборки.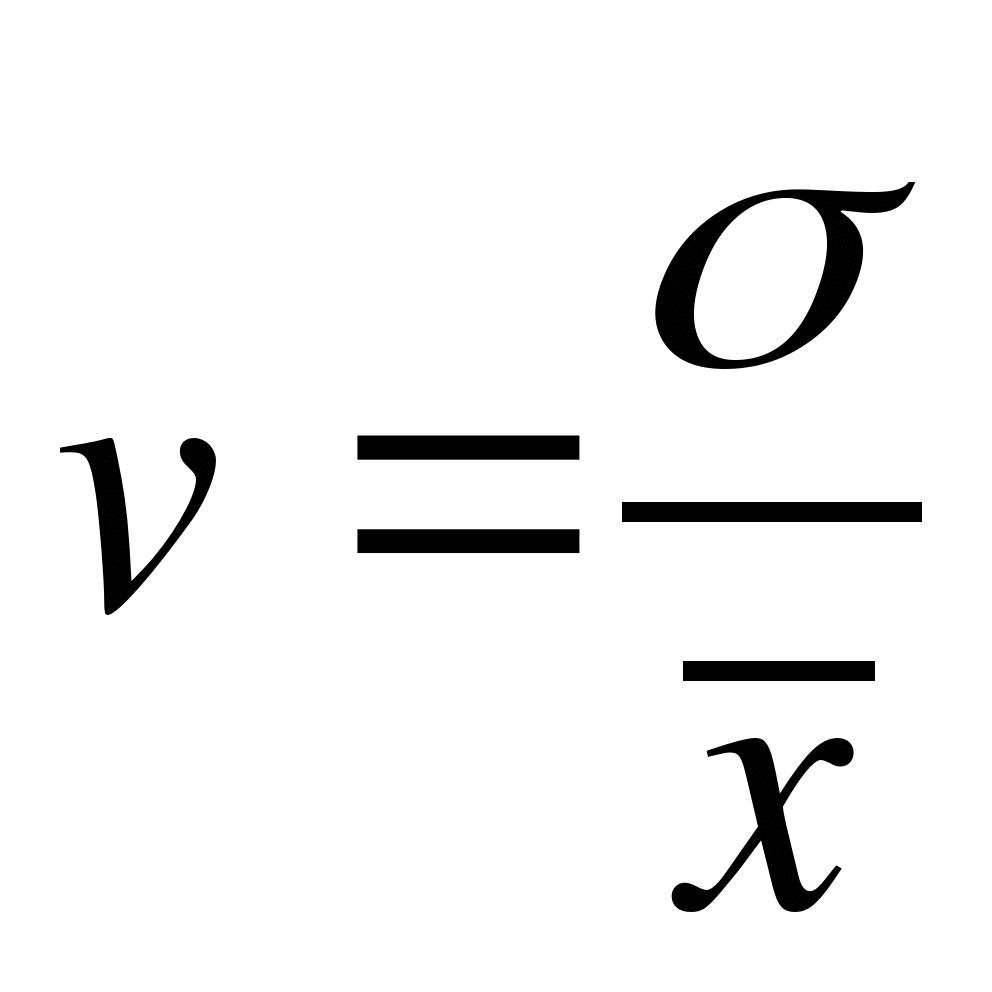
мк — среднее значение для популяции, такое же, как XBar в выборке.
Другими словами, чтобы найти коэффициент вариации, разделите стандартное отклонение на среднее значение и умножьте на 100.
Как найти коэффициент вариации в Excel.
Вы можете рассчитать коэффициент вариации в Excel, используя формулы для стандартного отклонения и среднего значения. Для заданного столбца данных (например, A1:A10) вы можете ввести: «=stdev(A1:A10)/average(A1:A10)) и умножить на 100.
Как найти коэффициент вариации вручную: шаги.
Пример вопроса : Учащимся предлагаются две версии теста. Один тест имеет заранее заданные ответы, а второй тест имеет рандомизированные ответы. Найдите коэффициент вариации.
| Обычный тест | Рандомизированные ответы | |
| Среднее | 50,1 | 45,8 |
| SD | 11,2 | 12,9 |
Шаг 1: Разделите стандартное отклонение на среднее значение для первой выборки:
11. 2 / 50,1 = 0,22355
2 / 50,1 = 0,22355
Шаг 2: Умножить шаг 1 на 100 :
0,22355 * 100 = 22,355%
Шаг 3: Разделите стандартное отклонение на среднее значение для второй выборки:
12,9 / 45,8 = 0,28166
Шаг 4: Умножить Шаг 3 на 100 :
0,28166 * 100 = 28,266%
Вот и все! Теперь вы можете напрямую сравнить два результата.
Загляните на наш канал YouTube, чтобы получить дополнительную справку по статистике и советы.
————————————————— ————————-Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице Facebook .
|
Конфиденциальность
Политика/Уведомление о безопасности
NIST — агентство США. Департамент торговли.
Дата создания: 24. |
Глава 4.4 Среднее значение, вариация, стандартное отклонение и коэффициент вариации — Животноводство
В статистических терминах непрерывные переменные описываются средним значением и мерами вариации. Для описания вариации можно использовать стандартное отклонение, дисперсию и коэффициент вариации.
Среднее значение рассчитывается следующим образом:
«Среднее» выборки представляет собой сумму значений выборки, деленную на количество элементов в выборке:
4, 36, 45, 50, 75
Дисперсия рассчитана следующим образом:
S 2 = σ (x I -x) / (N-1)
Стандартное отклонение рассчитывается следующим образом:
Например, стандартное отклонение представляет собой квадратный корень из дисперсии, и в этом случае для пяти значений: 4, 36, 45, 50, 75 вычисляется как:
N = 5 и среднее значение для x = 42
| x I | x I 6 -x | (x I -x) 2 | |
4 | -38 | 90 043||
36 | -6 | 36 | |
45 | 3 | 9 | |
50 | 8 | 64 | |
| 75 | 33 | +1089 | |
ΣX я = 210 | Σ (Х я — X) 2 = 2642 |
В этом случае дисперсия составляет 2642/4 = 660. 5, а стандартное отклонение равно √2642/5= 32,5
5, а стандартное отклонение равно √2642/5= 32,5
. Коэффициент вариации представляет собой стандартное отклонение, деленное на среднее значение, и рассчитывается следующим образом:
. коэффициент вариации: 32,5/42 = 0,77. Это означает, что размер стандартного отклонения составляет 77% размера среднего. Это означает, что вы видите много различий между животными, когда пять приведенных выше значений являются значением признака пяти животных.
Коэффициент вариации — значение, формула, примеры, использование
Коэффициент вариации является типом относительной меры дисперсии. Он выражается как отношение стандартного отклонения к среднему значению. Коэффициент вариации является безразмерной величиной и обычно выражается в процентах. Это помогает сравнить два набора данных на основе степени вариации.
Коэффициент вариации можно определить как для выборки, так и для генеральной совокупности. В таких отраслях, как финансы, коэффициент вариации используется, чтобы помочь инвесторам оценить соотношение риска и вознаграждения. В этой статье мы узнаем больше о коэффициенте вариации, его формуле и различных примерах.
В таких отраслях, как финансы, коэффициент вариации используется, чтобы помочь инвесторам оценить соотношение риска и вознаграждения. В этой статье мы узнаем больше о коэффициенте вариации, его формуле и различных примерах.
Что такое коэффициент вариации?
Коэффициент вариации является типом меры дисперсии. Мера дисперсии — это величина, которая используется для измерения степени изменчивости данных. Таким образом, коэффициент вариации используется для измерения отклонения данных от среднего или среднего значения.CV — это сокращенная форма коэффициента вариации.
Коэффициент вариации Определение
Коэффициент вариации представляет собой безразмерную относительную меру дисперсии, которая определяется как отношение стандартного отклонения к среднему значению. Если есть наборы данных с разными единицами, то лучший способ провести сравнение между ними — использовать коэффициент вариации.
Пример коэффициента вариации
Предположим, имеется набор данных [80, 90, 100]. Среднее значение равно 90, а стандартное отклонение населения равно 8,165. Коэффициент вариации равен 0,09. В процентном отношении коэффициент вариации составляет 9%.
Среднее значение равно 90, а стандартное отклонение населения равно 8,165. Коэффициент вариации равен 0,09. В процентном отношении коэффициент вариации составляет 9%.
Формула коэффициента вариации
Существуют две формулы для коэффициента вариации. Это коэффициент вариации совокупности и коэффициент вариации выборки. Население в статистике — это вся рассматриваемая группа. Другими словами, совокупность используется для обозначения полного набора данных.Когда из этой совокупности выбирается определенная часть, она называется выборкой. Выборка используется для представления всего населения исследования. Среднее значение генеральной совокупности и среднее значение выборки всегда будут одинаковыми. Однако, поскольку значение стандартного отклонения таким образом различается, существуют две формулы коэффициента вариации. Они приведены ниже:
- Коэффициент вариации населения = (\(\frac{\sigma}{\mu}\)) * 100.
- Примерный коэффициент вариации = \(\frac{s}{\mu}\) * 100
\(\сигма\) — стандартное отклонение генеральной совокупности. {2} }{Н — 1}}\)
{2} }{Н — 1}}\)
Как найти коэффициент вариации?
Формула коэффициента вариации особенно полезна в тех случаях, когда нам нужно сравнить результаты двух разных обследований, имеющих разные значения. В статистике формула коэффициента вариации (CV), также известная как относительное стандартное отклонение (RSD), представляет собой стандартизированную меру дисперсии распределения вероятностей или частотного распределения. Если значение коэффициента вариации ниже, то это указывает на меньшую изменчивость данных и высокую стабильность.Общие шаги для нахождения коэффициента вариации следующие:
- Шаг 1: Проверьте наличие набора образцов.
- Шаг 2: Рассчитать стандартное отклонение и среднее значение.
- Шаг 3: Подставьте значения в формулу коэффициента вариации, CV =\(\dfrac{σ}{µ}\) × 100, µ≠0,
Теперь давайте разберемся с этой концепцией на нескольких примерах.
Пример: Два завода C и D фабрики показывают следующие результаты о количестве рабочих и выплачиваемой им заработной плате.
| Число рабочих | 5000 | 6000 |
| Среднемесячная заработная плата | 2500 долларов | 2500 долларов |
| Стандартное отклонение | 9 | 10 |
Используя формулы коэффициента вариации, найдите, на каком заводе, C или D, наблюдается большая изменчивость индивидуальной заработной платы.
Решение:
Найти: какое растение имеет большую изменчивость.
Для этого нужно найти коэффициент вариации. Растение с более высоким коэффициентом вариации будет иметь большую изменчивость.
Коэффициент вариации для растения С.
Используя формулу коэффициента вариации,
CV = (σ/μ) × 100, μ≠0
CV = (9/2500) × 100
КВ = 0,36%
Теперь CV для завода D
CV = (σ/μ) × 100
CV = (10/2500) × 100
КВ = 0,4%
Завод C имеет CV = 0. 36, а растение D имеет CV = 0,4
36, а растение D имеет CV = 0,4
Ответ: Следовательно, завод D имеет большую изменчивость в индивидуальной заработной плате.
Коэффициент вариации и стандартное отклонение
Коэффициент вариации и стандартное отклонение используются, когда необходимо измерить разброс значений в наборе данных. Основные различия между двумя показателями приведены в таблице ниже.
| Коэффициент вариации | Стандартное отклонение |
| Относительная мера дисперсии | Это абсолютная мера дисперсии |
| Измеряет отношение стандартного отклонения к среднему | Он измеряет, насколько далеко точка данных находится от среднего |
| Коэффициент вариации обычно используется для сравнения вариации различных наборов данных | Стандартное отклонение используется для измерения разброса данных в одном наборе данных |
Коэффициент вариации Использует
Если необходимо сравнить два набора данных с одинаковыми значениями, можно использовать стандартное отклонение. Однако, если необходимо сравнить два набора данных с разными единицами измерения, необходимо использовать коэффициент вариации. Ниже приведены некоторые применения коэффициента вариации:
Однако, если необходимо сравнить два набора данных с разными единицами измерения, необходимо использовать коэффициент вариации. Ниже приведены некоторые применения коэффициента вариации:
- В финансовой сфере, если инвестор хочет инвестировать в конкретный ETF, он использует коэффициент вариации, чтобы выбрать тот, который обеспечит лучшее соотношение риска и доходности.
- Коэффициент вариации также используется для оценки согласованности данных. Распределение с меньшим коэффициентом вариации является более последовательным, чем распределение с большим CV.
Связанные статьи:
Важные замечания по коэффициенту вариации
- Коэффициент вариации — это относительная мера дисперсии, используемая для определения изменчивости данных.
- Выражается как отношение стандартного отклонения к среднему, умноженное на 100.
- Это безразмерная величина.
- Формула для коэффициента вариации имеет вид [\(\frac{\sigma}{\mu}\) * 100] или [\(\frac{s}{\mu}\) * 100].

Часто задаваемые вопросы о коэффициенте вариации
Что такое коэффициент вариации в статистике?
Коэффициент вариации – это безразмерная мера дисперсии, которая определяет степень изменчивости данных. Это очень полезно для сравнения двух наборов данных с разными единицами измерения.
Что такое хороший коэффициент вариации?
Допускается коэффициент вариации менее 20%. Для лабораторных результатов хороший коэффициент вариации должен быть меньше 10%.
Как рассчитать коэффициент вариации?
Чтобы рассчитать коэффициент вариации, выполните следующие действия.
- Найдите среднее значение данных.
- Найдите стандартное отклонение данных.
- Разделите стандартное отклонение на среднее значение и умножьте это значение на 100, чтобы получить коэффициент вариации.
В чем разница между стандартным отклонением и коэффициентом вариации?
Стандартное отклонение — это абсолютная мера дисперсии, используемая для определения разброса точек данных в одном наборе данных. Коэффициент вариации — это относительная мера дисперсии, с помощью которой можно сравнивать два набора данных с разными единицами измерения на основе изменчивости.
Коэффициент вариации — это относительная мера дисперсии, с помощью которой можно сравнивать два набора данных с разными единицами измерения на основе изменчивости.
Как интерпретировать коэффициент вариации?
Коэффициент вариации можно использовать для сравнения наборов данных, которые невозможно сравнить иначе. Высокий коэффициент вариации указывает на то, что уровень дисперсии вокруг среднего значения данных выше.
Является ли коэффициент вариации мерой дисперсии?
Коэффициент вариации является относительной мерой дисперсии.Он равен отношению стандартного отклонения к среднему и может быть выражен в процентах.
Является ли коэффициент вариации мерой центральной тенденции?
Нет, коэффициент вариации не является мерой центральной тенденции. Меры центральной тенденции включают среднюю медиану и моду. Коэффициент вариации является относительной мерой дисперсии.
Коэффициент вариации: определение и расчеты
Коэффициент вариации Определение
Коэффициент вариации является измерением вариации . Вариация — это мера того, насколько далеко от среднего варьируется набор данных. Коэффициент вариации не имеет единиц. Он используется с образцами, у которых разные единицы измерения или шкала измерения. Коэффициент вариации сравнивает стандартное отклонение со средним значением для каждого образца. Образцы должны быть неотрицательными.
Вариация — это мера того, насколько далеко от среднего варьируется набор данных. Коэффициент вариации не имеет единиц. Он используется с образцами, у которых разные единицы измерения или шкала измерения. Коэффициент вариации сравнивает стандартное отклонение со средним значением для каждого образца. Образцы должны быть неотрицательными.
Как рассчитать CV
Чтобы рассчитать коэффициент вариации, вам необходимо знать стандартное отклонение выборки (стандартное отклонение — это среднее значение того, насколько каждое значение данных из выборки отличается от своего среднего значения) и выборку среднее значение 90 221 (среднее значение — это мера центра, полученная путем сложения всех значений 90 219 x 90 222 в выборке и последующего деления на количество точек данных).
Стандартное отклонение выборки обычно обозначается строчными буквами s . Среднее значение выборки обычно представлено полосой размером 90 219 x 90 222 (90 219 x 90 222 с полосой над ней). Чтобы рассчитать CV, разделите стандартное отклонение на выборочное среднее, а затем умножьте на 100. При необходимости округлите CV до одного десятичного знака. Ваш ответ должен быть в процентах.
Чтобы рассчитать CV, разделите стандартное отклонение на выборочное среднее, а затем умножьте на 100. При необходимости округлите CV до одного десятичного знака. Ваш ответ должен быть в процентах.
Пример 1
Если образец A имеет среднее значение 100 долларов США и стандартное отклонение 10 долларов США, а образец B имеет среднее значение 300 фунтов и стандартное отклонение 20 фунтов, какая выборка имеет большую вариацию? Обратите внимание, что образцы A и Sample B имеют разные единицы измерения.
Образец a
10/100 = .1
.1 x 100 = 10%
Образец B
20/300 .067
.067 x 100 = 6,7%
Образец A имеет более высокий CV и поэтому больше вариаций.
Пример 2
Томас имеет среднее значение 20 очков за игру и стандартное отклонение 12 очков. Тодд набирал в среднем 12 очков за игру и стандартное отклонение 5 очков. У Тайлера было среднее значение 3 гола за игру и стандартное отклонение 2 гола.CV для Томаса будет (12 / 20) x 100 = 60%. CV для Тодда будет (5 / 12) x 100 = 41,7%. CV для Тайлера будет (2 / 3) x 100 = 66,7%. Поскольку у Тодда наименьший CV (41,7%), у него наименьшее количество вариаций и, следовательно, самый стабильный игрок.
CV для Тодда будет (5 / 12) x 100 = 41,7%. CV для Тайлера будет (2 / 3) x 100 = 66,7%. Поскольку у Тодда наименьший CV (41,7%), у него наименьшее количество вариаций и, следовательно, самый стабильный игрок.
Резюме урока
Когда вы сравниваете вариацию двух или более выборок, которые не имеют одинаковых единиц измерения, вы можете найти коэффициент вариации для каждой из выборок, а затем сравнить коэффициент вариации каждый образец.Чтобы найти коэффициент вариации для выборки, вы разделите значение стандартного отклонения 90 220 90 221 на значение 90 220 среднего 90 221 выборки, а затем умножите на сто. Коэффициент вариации будет в процентах. Чем меньше значение коэффициента вариации, тем меньшую вариацию имеет выборка.
Как рассчитать коэффициент вариации (CV)
Что такое коэффициент вариации?
Коэффициент вариации (CV) является мерой точности повторных измерений.В лаборатории он в основном используется для определения надежности анализов путем определения отношения стандартного отклонения к среднему значению. CV выражается в процентах, чтобы легко определить вариацию анализа.
CV выражается в процентах, чтобы легко определить вариацию анализа.
Что касается CV для анализов в лабораториях, существует два типа: внутри- и между- CV.
Intra CV — это изменение измерения образца в одном цикле. Например, измерение образца в двух или трех повторах на одной и той же пластине.Значения CV внутри анализа в идеале должны быть ниже 10% .
Inter -тест CV представляет собой вариацию измерения пробы в разных циклах. Например, измерение образца на одной пластине и того же образца на отдельной пластине. Значения CV между анализами в идеале должны быть меньше 15% .
Обычно значение CV внутри анализа ниже, чем CV между анализами, потому что вариация между сериями выше, чем в одной и той же серии.
Как рассчитать CV
Чтобы рассчитать CV, вам нужно знать среднее значение и стандартное отклонение для ряда измерений.Затем вы используете следующее уравнение:
Если для этого вы используете Microsoft Excel, вы можете использовать следующую формулу Excel. Просто измените «Значения» на интересующую вас серию чисел:
Просто измените «Значения» на интересующую вас серию чисел:
=(СТАНДОТКЛОН(значения)/СРЗНАЧ(значения))*100
Пример использования CV
Давайте рассмотрим пример, чтобы лучше понять расчет.
Представьте, что мы только что провели иммуноферментный анализ (ELISA) для расчета концентрации белка X в том же образце плазмы.Мы измеряли один и тот же образец три раза на пластине и на трех разных пластинах (пластины 1, 2 и 3). Вот наши данные:
Сначала рассчитайте среднее (среднее) между показаниями 1-3 на каждой пластине:
Затем мы используем приведенную выше формулу CV в Excel для расчета CV внутри анализа для каждого планшета. Это разброс измерений одной и той же пластины (между показаниями 1, 2 и 3):
Наконец, мы можем рассчитать CV между и анализами между средними значениями из трех планшетов.Это указание на разброс одних и тех же показаний на разных пластинах:
Как вы можете видеть, CV внутри анализа намного ниже, чем CV между анализом . Поскольку CV внутри и между анализами меньше, чем 10% и 15% соответственно, это указывает на небольшую величину вариации между измерениями.
Поскольку CV внутри и между анализами меньше, чем 10% и 15% соответственно, это указывает на небольшую величину вариации между измерениями.
Коэффициент вариации и коэффициент Шарпа
Коэффициент вариации (CV) представляет собой отношение стандартного отклонения данных к его среднему значению.Это дает нам значение риска на единицу прибыли.
CV = s/X
, где s — стандартное отклонение выборки, а X — среднее значение выборки.
Чем выше коэффициент вариации; тем более рискованной является ценная бумага, потому что мы берем на себя больший риск на единицу прибыли.
Коэффициент Шарпа — это отношение превышения доходности над безрисковой ставкой к стандартному отклонению. Это дает нам значение избыточной доходности на единицу риска.
S h = (R-bar p — R-bar f )/s p
, где R-bar p — средняя доходность портфеля, R-bar f — средняя доходность безрискового актива, а s p — стандартное отклонение доходности портфеля.
Чем выше коэффициент Шарпа; тем лучше портфель, потому что мы получим более высокую среднюю избыточную доходность на единицу риска.
Пример 11: Расчет коэффициента вариации и Шарпа | |||||||||||||||||||||||||||
Средняя доходность и стандартное отклонение двух портфелей приведены ниже:
Рассчитайте коэффициент вариации и коэффициент Шарпа портфелей. Решение:
Обратите внимание, что мы получаем разные результаты из коэффициента Шарпа и коэффициента вариации.Портфель А лучше по коэффициенту Шарпа, а портфель Б лучше по коэффициенту вариации. 2019 © Все права защищены. |

 Учитывая набор
измерений температуры, коэффициент вариации на
Шкала Цельсия будет отличаться от коэффициента вариации
по шкале Фаренгейта.
Учитывая набор
измерений температуры, коэффициент вариации на
Шкала Цельсия будет отличаться от коэффициента вариации
по шкале Фаренгейта.
 2\) — дисперсия логарифма данных.
2\) — дисперсия логарифма данных. Шаг 1. Создайте данные
.
пропустить 25
читать gear.dat y x
пропустить 0
установить запись десятичных знаков 6
.
. Шаг 2: Определите управление графиком
.
заглавный регистр
смещение заголовка 2
этикетка чехол asis
.
y1label Коэффициент вариации
x1label Группа
title Коэффициент вариации для GEAR.DAT
пусть ngroup = уникальный x
xlimits 1 группа
основной номер метки x1tic ngroup
минор x1tic знак номер 0
данные о единицах смещения метки деления
x1tic смещение метки 0,5 0,5
y1tic метка десятичных знаков 3
.
символ Х
пустая строка
.
установить среднее значение опорной линии статистического графика
.график коэффициента вариации y x
Шаг 1. Создайте данные
.
пропустить 25
читать gear.dat y x
пропустить 0
установить запись десятичных знаков 6
.
. Шаг 2: Определите управление графиком
.
заглавный регистр
смещение заголовка 2
этикетка чехол asis
.
y1label Коэффициент вариации
x1label Группа
title Коэффициент вариации для GEAR.DAT
пусть ngroup = уникальный x
xlimits 1 группа
основной номер метки x1tic ngroup
минор x1tic знак номер 0
данные о единицах смещения метки деления
x1tic смещение метки 0,5 0,5
y1tic метка десятичных знаков 3
.
символ Х
пустая строка
.
установить среднее значение опорной линии статистического графика
.график коэффициента вариации y x
 01.2017
01.2017 
 Предположим, что средняя безрисковая ставка равна 5 процентам.
Предположим, что средняя безрисковая ставка равна 5 процентам. 00 процентов
00 процентов