Трудоемкость работ. Определение, расчет, формула
Содержание страницы
- Что такое трудоемкость
- Порядок расчета трудоемкости
- Трудоемкость ремонтных работ
- Как снизить трудоемкость
- Методы увеличения производительности труда
Управление ресурсами – ключевой элемент для обеспечения нормального функционирования предприятия. Расход трудового ресурса на производство продукции можно измерить. Для этого требуется определенная формула.
Управление персоналом представляет собой деятельность людей, выполняющих на предприятии или в организации функции, способствующие наиболее эффективному использованию человеческих ресурсов для достижения первичных целей предприятии (организации).
Кто в компании занимается управлением персоналом?
Что такое трудоемкость
Трудоемкость – это показатель, который позволяет проанализировать соотношение трат ресурсов и времени. Значение отображает время, которое нужно потратить на производство единицы товара.
Рассмотрим, что именно дает определение трудоемкости работы:
- Определение влияния трудовых затрат на количество готового товара.
- Определение резервов для увеличения производительности труда.
- Выявление возможностей для эффективной организации использования ресурсов.
- Установление областей, где трудовые ресурсы применяются наиболее продуктивно.
Трудоемкость работы рекомендуется вычислять на регулярной основе. Это позволит сравнить результаты, проанализировать динамику.
Какие виды трудоемкости выделяют в зависимости от состава трудовых затрат и их роли в процессе производства?
Порядок расчета трудоемкости
В ходе расчетов используется следующая формула: Тр = Кч / Сп.
В рамках формулы фигурируют эти значения:
- Тр – трудоемкость.
- Кч – совокупный фонд времени в человеко-часах.
- Сп – совокупная стоимость изготовленной продукции.
Существует также такая формула: Т = Рв / Кп.
В формуле используются эти значения:
- Т – трудоемкость.
- Рв – рабочее время.
- Кп – число изготовленной продукции.
Рассмотрим подробнее алгоритм расчетов. Сначала нужно определить совокупный объем времени, отработанного сотрудниками за отчетный период (как правило, это месяц). В расчетах фигурирует время, отработанное фактически. Определить его можно исходя из информации, изложенной в первичных документах. К примеру, это может быть табель пользования временем по конкретным цехам. Затем нужно определить совокупность отработанных человеко-часов за интересующий период. Во внимание принимается только труд сотрудников, которые являются основными. Это специалисты, оформленные официально и работающие на полную ставку.
Затем вычисляется стоимость товара, который был изготовлен компанией. Также нужно учитывать поступление готовой продукции. В расчетах будет фигурировать планово-учетные цены товара. Определяются они исходя из информации, содержащейся в бухучете. Необходимо разделить реальный фонд времени в человеко-часах на стоимость изготовленного товара. Значение, полученное по итогам расчетов, считается коэффициентом трудоемкости.
Выполняется анализ полученных значений. Процедура включает в себя следующие этапы:
- Чем ниже трудоемкость, тем большей будет производительность труда сотрудников.
- Проверка исполнения плана по производству.
- Установление отклонений от плановых значений.
- Определение воздействия разных факторов на увеличение или уменьшение производительности.
- Подведение итогов.
На производительность может влиять качество сырья, подготовка сотрудников.
ВАЖНО! Уменьшение трудоемкости работ способствует экономии ресурсов. Это снижает себестоимость товара, благотворно влияет на извлечение прибыли.
Это снижает себестоимость товара, благотворно влияет на извлечение прибыли.
Трудоемкость ремонтных работ
Расчет трудоемкости ремонтных работ имеет свои нюансы. В частности, значение трудоемкости определяется сложностью использованного оборудования. Техника, используемая предприятием, подразделяется на группы с различной ремонтной сложностью. Уровень сложности присваивается каждому конкретному объекту. Для присвоения уровня объект сравнивается с агрегатом-эталоном. Единицей измерения трудоемкости является условная единица, отражающая затрату времени на исполнение одной операции.
Рассмотрим нормативы времени:
- Осмотр: 0,1 ч/час.
- Текущие ремонтные работы: 5 ч/час.
- Капитальные работы: 40 ч/час.
Трудоемкость ремонта определяется исходя из этой формулы: T = R * q * n.
В формуле фигурируют эти значения:
- R – группа ремонтной сложности.
- Q – трудоемкость условной единицы (человеко-часы).
- N – число ремонтов данной техники.

Рассмотрим примеры расчетов для однокривошипных прессов:
- 10 * 0,1 * 3 = 3 человеко-часов.
- 10 * 5 * 2 = 100 человеко-часов.
В расчетах трудоемкости работы фигурируют только основные сотрудники. Кто это? Основными трудящимися являются обычные трудящиеся без квалификации, специалисты, управленческий состав. Основание для расчета количества сотрудников – это трудоемкость ремонта техники, нормы обслуживания и баланс трудового времени. Последний представляет собой объем часов, отрабатываемый одним сотрудником в рамках расчетного периода.
Как снизить трудоемкость
Как уже было написано ранее, главная цель руководителя – снижение трудоемкости. Нужно это для извлечения максимальной прибыли при минимуме ресурсов. Достичь поставленной цели можно следующими путями:
- Использование современных технологий.
- Повышение эффективности организации труда.
- Использование качественного сырья.
- Внедрение в производство современного оборудования.

Все эти меры позволят повысить объемы изготовленной продукции при снижении трудоемкости.
Как снизить трудоемкость учета материалов?
Методы увеличения производительности труда
Рассмотрим основные факторы увеличения производительности труда:
- Автоматизация производства, модернизация уже имеющейся техники, улучшение качества сырья.
- Изменение организации производства и труда, перемена специализации деятельности, улучшение управления производством, уменьшение потерь рабочего времени, уменьшение объема брака и отклонений.
- Природные условия: расположение нефти и угля, содержание нужного элемента в рудах, перемена глубина разработки.
- Изменение масштабов производства, снижение численности сотрудников.
- Перемена структуры производства: изменение веса полуфабрикатов, методов изготовления.
Руководителю нужно разработать конкретные стратегии уменьшения трудоемкости. Раз в выбранный период нужно рассчитывать трудоемкость работы. Требуется это для отслеживания динамики значений.
Требуется это для отслеживания динамики значений.
Как рассчитать трудоемкость: формула проста :: SYL.ru
Трудоемкость (формула которой позволяет рассчитать, сколько труда будет вложено в тот или иной комплекс работ) помогает выявить структуру затрат времени и сил. Также она дает возможность определить, насколько может вырасти производительность работы, чтобы обеспечить наиболее рациональное использование человеческих ресурсов и сил.
Как рассчитать трудоемкость?
Чаще всего она представляется как показатель, который указывает на сумму затрат труда (за некоторый период времени), что были потрачены на производство одной единицы товара или проведения одной рабочей операции.
Трудоемкость, формула расчета которой помогает установить прямую зависимость между трудовыми затратами и объемом производимой продукции, рассчитывается таким образом:
- Q = T : V.
Как расшифровать расчет трудоемкости?
В вышеприведенной формуле основную задачу берет на себя Q. Эта переменная и является тем количеством затрат на единицу, которую производят за час. При этом следует понимать, что расчет трудоемкости — дело достаточно сложное и требующее особого внимания. Дело в том, что на сегодняшний день существуют различные ее виды, которые рассчитываются с помощью разных формул.
Эта переменная и является тем количеством затрат на единицу, которую производят за час. При этом следует понимать, что расчет трудоемкости — дело достаточно сложное и требующее особого внимания. Дело в том, что на сегодняшний день существуют различные ее виды, которые рассчитываются с помощью разных формул.
Виды трудоемкости
В современном мире существует восемь ее отдельных видов, расчет каждой из которых отличается использованием совершенно другой формулы. При этом большинство людей, которые сталкиваются с данной проблемой, стараются прежде всего определить, какой вид им необходимо рассчитать.
Трудоемкость делится на:
- Технологическую.
- Обслуживания.
- Производственную.
- Управления.
- Полную.
- Нормативную.
- Фактическую.
- Плановую.
Технологическая, производственная и полная трудоемкости
Технологический вид, формула которого лишь в некоторой степени отличается от классической, может быть определен теми затратами труда, которые были произведены и повременщиками, и сдельщиками. Кроме этого, величину можно без проблем рассчитать с помощью производственных операций, готовых изделий, отдельных деталей и узлов.
Кроме этого, величину можно без проблем рассчитать с помощью производственных операций, готовых изделий, отдельных деталей и узлов.
Производственная трудоемкость, формула которой определяется с помощью расчета труда вспомогательных и основных рабочих, представляет собой совокупность технологического ее вида с обслуживанием.
Полная трудоемкость, формула которой выглядит следующим образом:
- Q полн. = T вспом.раб. + T осн.раб. + T раб.упр. = Q упр. + Q произв.,
позволяет отразить в себе все затраты труда для изготовления одной единицы продукции. Она является наиболее серьезной.
Трудоемкости обслуживания и управления
В трудоемкость обслуживания можно внести все те затраты труда, которые были произведены вспомогательными рабочими. При этом все сотрудники должны быть занятыми в сферах обслуживания производства целиком. Расчет такой емкости труда производится с помощью всех операций, изделий и услуг.
В трудоемкость управления внесены затраты труда охраны, специалистов и руководителей.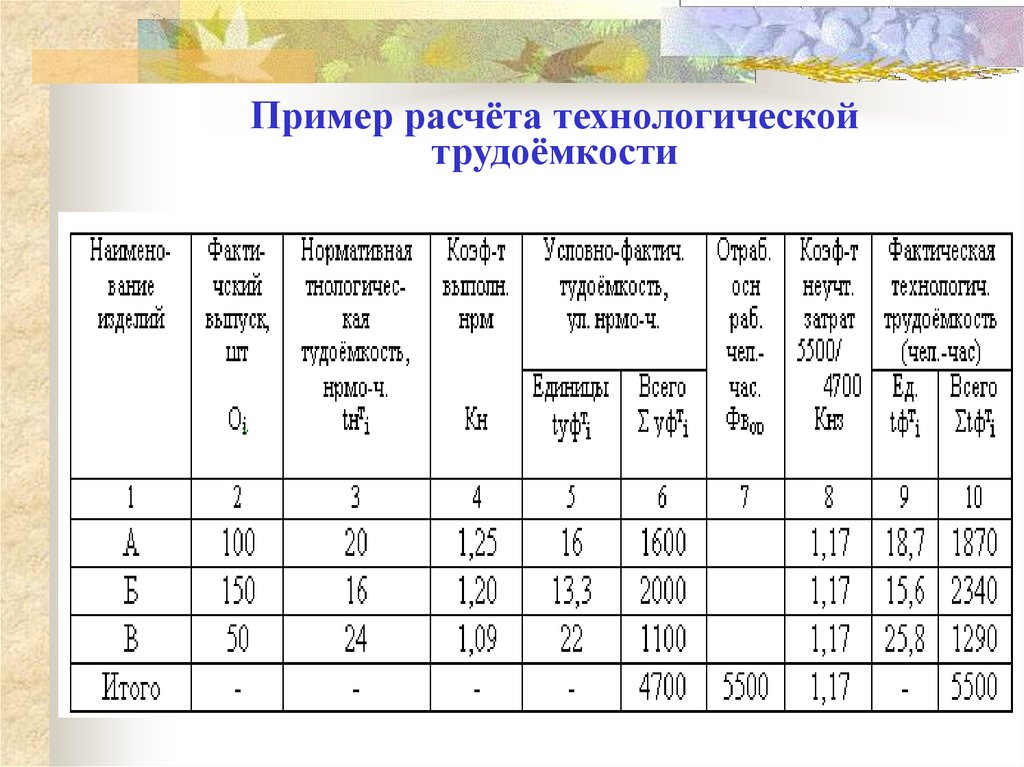 При этом труды каждого из них будут рассчитываться по-разному. Те затраты труда, которые непосредственно связаны с изготовлением изделия, будут относиться именно к этим изделиям, та же часть, которая не связана с ними, будет относиться к пропорциональной производительности.
При этом труды каждого из них будут рассчитываться по-разному. Те затраты труда, которые непосредственно связаны с изготовлением изделия, будут относиться именно к этим изделиям, та же часть, которая не связана с ними, будет относиться к пропорциональной производительности.
Нормативная, фактическая и плановая трудоемкости
Нормативная трудоемкость, формула которой рассчитывается при помощи главных норм труда (времени обслуживания, времени выработки, численности и т. д.), позволяет определить общую величину затрат времени и сил, которые необходимы для создания какого-либо изделия или же всей программы полностью.
Под фактической трудоемкостью понимается такая, формула которой вносит в себя все те затраты труда, что уже были произведены. При этом принимается во внимание объем работы или выпуск продукции.
Плановая трудоемкость немного ниже, чем нормативная. Но при этом в нее входят запланированные затраты, которые всегда должны иметь место, когда что-то вырабатывается.
Трудоемкость работ (формула которой каждый раз определяется с помощью расчета потраченного времени на производство одной единицы) позволяет измерить производительность и тем самым выявить резервы возможного роста.
Что такое производительность труда?
Трудоемкость (формула расчета которой была рассмотрена выше) часто влияет на изготовление товара или проведение операции. Понятие производительности труда включает в себя показатели плодотворности деятельности всех работников предприятия. Ее при этом можно измерить с помощью количества выполненной работы (изготовленных изделий или предоставленных услуг), которая была проделана за некоторое определенное время. При этом с помощью данного понятия можно определить, насколько хорошо работник справляется с необходимостью создавать при помощи своего труда товары, услуги и другую продукцию за час, неделю, месяц, год и т. д. В современном мире то количество работы, которое было произведено одним работником, принято называть отдельным понятием — «выработка». С помощью показателей выработки владелец предприятия может измерить ту работу, которую провел каждый сотрудник в определенный период времени. При этом нет особой разницы, было ли это оказание услуг или производство товара.
С помощью показателей выработки владелец предприятия может измерить ту работу, которую провел каждый сотрудник в определенный период времени. При этом нет особой разницы, было ли это оказание услуг или производство товара.
Измерители производительности труда
Среди самых главных измерителей стоит выделить такие:
- Стоимостные — в этом случае используется так называемый индексный метод, когда сопоставляется производительность за разные периоды времени.
- Натуральные — они могут применяться только в том случае, если предприятие длительный период времени изготавливает всего лишь один вид продукции.
- Условно-натуральные — могут быть применимы даже в том случае, если на предприятии изготавливается различная продукция. Но в этом случае один ее вид будет выбран в качестве условного, и вся остальная продукция будет сводится к этому коэффициенту.
- Трудовые — они применимы в том случае, если необходимо рассчитать производительность труда в разных подразделениях одного предприятия.

Производительность труда можно без проблем рассчитать с помощью специальной формулы:
- П = О : Ч,
где «О» означает объем выполненной работы одним сотрудником за определенное количество времени, а «Ч» является общим числом всех работников, которые работают на данном предприятии.
Чтобы производительность труда можно было определить с максимально возможной точностью, специалисты рекомендуют обратить внимание на некоторое важные требования. Среди них следует выделить такие:
- Учитывайте весь труд, затраченный на один определенный вид работ.
- Следует обязательно устранять возможные искажения, которые могут быть связаны с некоторыми различиями в емкости труда.
- Исключите возможность подсчета затрат труда повторно, когда учитывается прошлый труд.
- Соизмеряйте возможные изменения в производительности труда в связи с увеличением или уменьшением средней заработной платы сотрудника.
Иногда в зарубежной практике, кроме производительности труда, используют термин «показатель производительности».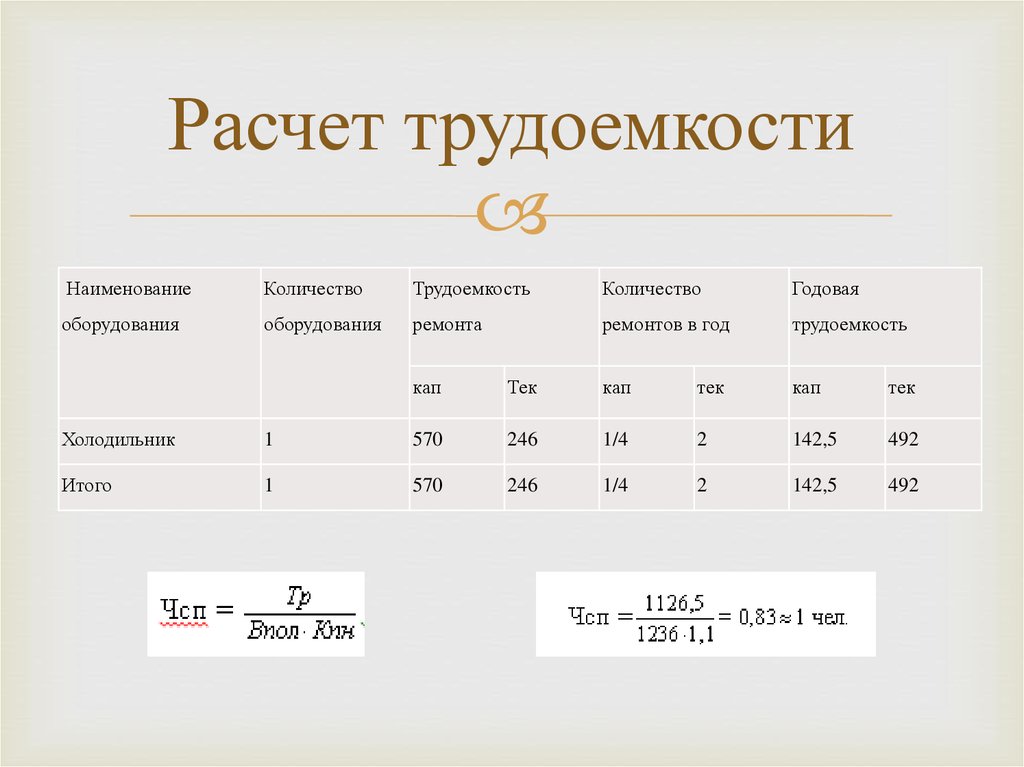 Чтобы рассчитать его, следует принимать во внимание не только затраты труда на изготовление той или иной продукции, но и те ресурсы, которые были использованы в процессе изготовления (это может быть земля, оборотный и основной капиталы).
Чтобы рассчитать его, следует принимать во внимание не только затраты труда на изготовление той или иной продукции, но и те ресурсы, которые были использованы в процессе изготовления (это может быть земля, оборотный и основной капиталы).
4.2: Сложность формул — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 9701
- Кристофер Лири и Ларс Кристиансен
- SUNY Geneseo и Университет Осло через OpenSUNY
Работаем на языке теории чисел
\[\mathcal{L}_{NT} = \{ 0, S, +, \cdot, E, < \},\]
, и мы продолжим работать на этом языке в следующих нескольких главах. \(\mathfrak{N}\) — стандартная модель натуральных чисел,
\[\mathfrak{N} = \left( \mathbb{N}, 0, S, +, \cdot, E, < \right),\]
, где функции и отношения — это обычные функции и отношения, которые вы знали с тех пор, как были по колено перед кузнечиком.
Один из способов думать о простейших формулах языка натуральных чисел (на самом деле любого языка) — это формулы, которые не содержат никаких кванторов. Кажется естественным, что формула \(S0 = y\) проще, чем \(\forall x S 0 = y\). На один маленький шаг сложнее бескванторных формул являются формулы, содержащие то, что мы будем называть ограниченными кванторами:
Определение 4.2.1.
Если \(x\) — переменная, не входящая в терм \(t\), условимся использовать следующие сокращения:
\[ \left( \forall x < t \right) \phi \: \text{means} \: \forall x \left( x < t \rightarrow \phi \right) \\ \left( \forall x \leq t \right) \phi \: \text{means} \: \forall x \left( \left( x < t \lor x = t \right) \rightarrow \phi \right) \\ \left( \ существует x < t \right) \phi \: \text{means} \: \exists x \left( x < t \land \phi \right) \\ \left( \exists x \leq t \right) \phi \: \text{means} \: \exists x \left( \left( x < t \lor x = t \right) \land \phi \right).
Эти сокращения составят набор из ограниченных кванторов .
Таким образом, формула \(\exists x \left( \left( \forall y < \overline{42} \right) y = Sx \right)\) является формулой с одним ограниченным квантором и одним неограниченным квантором.
Помните, что наша цель состоит в том, чтобы создать предложение, истинное в \(\mathfrak{N}\) и недоказуемое из нашего набора аксиом. Можем ли мы найти такую формулу, которая содержит только ограниченные кванторы? Это было бы очень здорово, но, к сожалению, этого не произойдет. Помните наш набор аксиом \(N\) из раздела 2.8? Если вы вернетесь к этому разделу, вы увидите, что все эти аксиомы являются истинными утверждениями о натуральных числах, поэтому они должны быть следствием любого потенциального набора аксиом для \(Th \left( \mathfrak{N} \right) \). Но \(N\) на самом деле довольно сильный набор утверждений. В частности, \(N\) достаточно надежен, чтобы доказать каждое истинное утверждение о \(\mathfrak{N}\), содержащее только ограниченные кванторы.
Определение 4.2.2.
Набор из \(\Sigma\)-формул определяется как наименьший набор \(\mathcal{L}_{NT}\)-формул такой, что:
- Каждая атомарная формула является \( \Сигма\)-формула.
- Каждое отрицание атомарной формулы является \(\Сигма\)-формулой.
- Если \(\alpha\) и \(\beta\) являются \(\Sigma\)-формулами, то \(\alpha \land \beta\) и \(\alpha \lor \beta\) являются \ (\Сигма\)-формулы.
- Если \(\alpha\) является \(\Sigma\)-формулой, а \(x\) является переменной, не входящей в терм \(t\), то следующие \(\Sigma\ )-формулы: \(\left( \forall x < t \right) \alpha\), \(\left( \forall x \leq t \right) \alpha\), \(\left( \exists x < t \right) \alpha\), \(\left( \exists x \leq t \right) \alpha\).

- Если \(\alpha\) является \(\Sigma\)-формулой и \(x\) является переменной, то \(\left( \exists x \right) \alpha\) является \(\Sigma \)-формула.
Позже мы докажем (теорема 5.3.13), что на самом деле наш набор аксиом \(N\) достаточно силен, чтобы доказать каждое истинное \(\Sigma\)-предложение, так что даже эти формулы недостаточно сложны, чтобы установить результат незавершенности. Однако, если вместо того, чтобы допустить неограниченный квантор существования, мы допустим неограниченный квантор всеобщности, ситуация изменится.
Определение 4.2.3.
Совокупность \(\Pi\)-формул есть наименьшее множество \(\mathcal{L}_{NT}\)-формул такое, что:
- Каждая атомарная формула является \(\Pi \)-формула.
- Каждое отрицание атомарной формулы является \(\Pi\)-формулой.
- Если \(\alpha\) и \(\beta\) являются \(\Pi\)-формулами, то \(\alpha \land \beta\) и \(\alpha \lor \beta\) являются \ (\Pi\)-формулы.

- Если \(\alpha\) является \(\Pi\)-формулой, а \(x\) является переменной, не входящей в терм \(t\), то следующие \(\Pi\ )-формулы: \(\left( \forall x < t \right) \alpha\), \(\left( \forall x \leq t \right) \alpha\), \(\left( \exists x < t \right) \alpha\), \(\left( \exists x \leq t \right) \alpha\).
- Если \(\alpha\) является \(\Pi\)-формулой и \(x\) является переменной, то \(\left( \forall x \right) \alpha\) является \(\Pi \)-формула.
Итак, в то время как множество \(\Sigma\)-формул замкнуто относительно ограниченной квантификации и неограниченной экзистенциальной квантификации, совокупность \(\Pi\)-форм замкнута относительно ограниченной квантификации и неограниченной универсальной квантификации.
Главный результат оставшейся части книги, первая теорема Гёделя о неполноте, утверждает, что если нам дан любой непротиворечивый и разрешимый набор аксиом, то будет \(\Pi\)-формула \(\sigma\) такая что \(\sigma\) является верным утверждением о натуральных числах, но из наших аксиом формулы \(\sigma\) не следует вывода. Таким образом, наш набор аксиом должен быть неполным. Достижение этой теоремы займет у нас все оставшееся время.
Таким образом, наш набор аксиом должен быть неполным. Достижение этой теоремы займет у нас все оставшееся время.
Вы могли заметить, что каждое отрицание \(\Sigma\)-формулы логически эквивалентно \(\Pi\)-формуле, и наоборот (см. упражнение 3). Если мы возьмем пересечение набора \(\Sigma\)-формул и набора \(\Pi\)-формул, мы получим \(\Delta\)-формул:
Определение 4.2.4.
Набор \(\Delta\)-формул является пересечением набора \(\Sigma\)-форм с множеством \(\Pi\)-формул.
Таким образом, в каждой \(\Delta\)-формуле все кванторы ограничены. Выяснится, что наш таинственный (ну, на самом деле не такой уж и загадочный) набор аксиом \(N\) достаточно силен, чтобы доказать любую истинность в-\(\mathfrak{N}\) \(\Delta\ )-формулы и опровергнуть каждую ложную-в-\(\mathfrak{N}\) \(\Delta\)-формулу. Это будет очень важно для нас.
- Ссылаясь на определение 4.2.2, объясните подробно, почему следующие формулы являются (или не являются) \(\Sigma\)-формулами.

(a) \(S0 + S0 = SS0\)
(b) \(\neg \left( 0 < 0 \lor 0 < S0 \right)\)
(c) \(\left( \forall x < \overline{17} \right) x < \overline{17}\)
(d) \(S0 \cdot S0 = S0 \land \left( \exists y < x \right) \left( \exists z < y \right) y + z = x\)
(e) \(\left( \forall y \right) \left( y < 0 \rightarrow 0 = 0 \right)\)
(f) \(\left( \существует x \справа) \слева( x < x \справа)\) - Давайте определим набор классных формул как наименьший набор \(\mathcal{L}_{NT}\)-формул, который:
(a) Содержит все атомарные формулы.
(b) Содержит все отрицания атомарных формул.
(c) Замкнут под связками \(\land\) и \(\lor\).
(d) Замкнут относительно ограниченных кванторов и квантора \(\существует\)
Докажите, что формула классная тогда и только тогда, когда формула является \(\Сигма\)-формулой. (Четыре приведенных выше условия иногда используются для определения набора \(\Sigma\)-формул. Вы только что доказали, что данное здесь определение эквивалентно определению 4. 2.2.)
2.2.) - Подумайте о \(\Sigma\)-формуле
\[\alpha \: \text{is} \: x< y \lor \left( \forall z < w \right) x + \overline{17} = \overline{42}.\]
(a) Является ли \(\alpha\) \(\Pi\)-формулой?
(b) Является ли \(\neg \alpha\) \(\Pi\)-формулой?
(c) Можете ли вы найти \(\Pi\)-формулу, эквивалентную \(\neg \alpha\)?
(d) Тщательно докажите, что если \(\alpha\) является любой \(\Sigma\)-формулой, то \(\neg \alpha\) логически эквивалентна \(\Pi\)-формуле.
Эта страница под названием 4.2: Сложность формул распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Кристофером Лири и Ларсом Кристиансеном (OpenSUNY) посредством исходного контента, который был отредактирован в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Кристофер Лири и Ларс Кристиансен
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- №
- Теги
- source@https://milneopentextbooks.
 org/a-friendly-introduction-to-mathematical-logic
org/a-friendly-introduction-to-mathematical-logic
- source@https://milneopentextbooks.
логика — Связь между сложностью формулы и сложностью кодирования доказательства формулы набор кодов данной формулы тривиален независимо от формулы. 9\mathbb{N}$ тогда и только тогда, когда $\mathbb{N}\models\forall x(\chi_1(x)\iff\chi_2(x))$.)
Тогда мы можем спросить, какова сложность $EC(\ varphi)$ связано со сложностью $\varphi$. Это априори более значимо.
Однако оказывается, что это все еще тривиально в точном смысле, и действительно кажется трудным сформулировать свой вопрос таким образом, чтобы избежать таких проблем.
Начнем с оптимизма. Следующее наблюдение позволяет предположить, что между $EC(\varphi)$ и $\varphi$ может существовать интересное отношение сложности: 9\mathbb{N}$. $\quad\Box$
Однако оказывается, что это тривиально:
- Факт $2$ : Независимо от того, что такое $\varphi$, $EC(\varphi)$ имеет ту же сложность, что и истинный первый -порядковая теория арифметики, $Th(\mathbb{N})$.








 2.2.)
2.2.) org/a-friendly-introduction-to-mathematical-logic
org/a-friendly-introduction-to-mathematical-logic